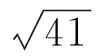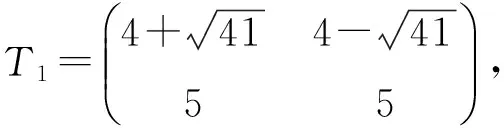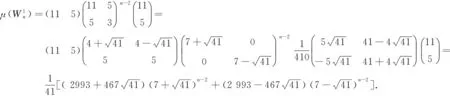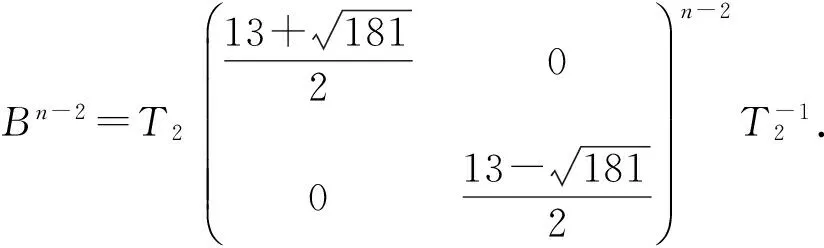五边形链的Hosoya指标*
田文文 , 杨 斐, 田双亮
(西北民族大学 a.数学与计算机科学学院;b.中国民族信息技术研究院 兰州 730030)
五边形链的Hosoya指标*
田文文a, 杨 斐b, 田双亮c
(西北民族大学 a.数学与计算机科学学院;b.中国民族信息技术研究院 兰州 730030)
Hosoya指标是化学分子图论研究中较为流行和重要的拓扑指标之一,主要对五边形链在不同构联接位下的Hosoya指标进行了研究,并给出了更为一般的计算公式.
五边形链;Hosoya指标;计算公式
0 引 言
Hosoya指标是由日本化学家Haruo Hosoya于1971年在文献[2]中提出并进行研究的,它表示图G中所有匹配的数目,记为μ(G).该指标与物质的沸点、熵、化学键的计算和化学结构等有着密切的联系,且有着较为广泛的应用,相关的应用参见文献[3-5].文献[7]中研究了五角链关于k-匹配的极端情形,并得出了相应的极图.本文通过n个五边形在不同构联接位下构造了两类特殊的五边形链,并且研究了这两类五边形链的Hosoya指标,给出了具体表达式.
设G=(V,E)是一个简单图,它的点集和边集分别为V(G)和E(G).令e和x分别为图G的一条边和一个顶点,用G-e表示图G删去边e得到的图,用G-x表示图G删去顶点x(及关联的边)得到的图.若B⊆E(G),对任意的两条边e1,e2∈B,且e1与e2无公共顶点,则称B为图G的一个匹配,其中空集为任何图的一个匹配.本文中Fn表示Fibonacci数,即满足:Fn=Fn-1+Fn-2,n≥2,且F0=0,F1=1.文中未加说明的符号及术语参见文献[1].
定义1 设Q1,Q2,…,Qn为n个五边形构成的序列.则称该序列为五边形链,记为Wn,如果满足:
(i) 对任意的1≤s (ii) 每个正方形与割边的顶点都为3度顶点. 用Φn表示含有n个五边形构成的五边形链的全体.设Wn∈Φn,则五边形链Wn(n≥2)可由Wn-1再联接一个五边形得到,而每个链中的五边形都有4个可联接位,其中与接点距离相等的两个可联接位是同构的,所以只有两种非同构的联接方式:Wn-1→[Wn-1]k=Wn,其中k=1,2,分别称为1-位联接和2-位联接,如图1所示。 图1 两种联接方式 图2 五边形链和 在证明主要结论之前,先给出文献[4]中的几个相关引理如下: 引理1 设G是一个简单图,对任意的u,v∈V(G),uv∈E(G),有μ(G)=μ(G-uv)+μ(G-u-v). 引理3 对于n阶的路Pn,有μ(Pn)=Fn+1. 引理4 对于n阶的圈Cn,有μ(Cn)=Fn+1+Fn-1. 定理1 对任意的正整数n≥2,有: 证明(i) 如图2所示,根据引理1可得: 改革开放40年,随着社会主义市场经济的确立和经济的快速发展,今日之中国已成为世界第二大经济体,与此相适应的社会变迁正在使转型中的中国社会处于深刻变革之中。为适应新形势下全面深化改革的需要,中共十八届三中全会通过对以往创新社会管理实践探索的理论提升,对创新社会治理、改进社会治理方式提出了新的要求。从创新管理到创新治理,意味着党的治国理政方略在处理国家与社会之关系上的重大转变,即由自上而下政府一元主导的社会管理向政府主导多元主体协同共建共治的系统治理的转变。 所以 从而 (ii) 如图2所示,根据引理1可得: 所以 从而 定理2 对任意的正整数n≥2,有: 从而 [1] BONDY J A,MURTY U S R.Graph theory with applications[M].New York:The Macmillan Press,1976. [2] HOSOYA H.Topological index[J].Bull Chem Soc Japan,1971,44:2332-2339. [3] MERRFIELD R E,SIMMONS H E.Topological Methods in Chemistry[M].New York:Wiley,1989. [4] GUTMAN I,POLANSKY O E.Mathematical Concepts in Organic Chemistry[M].Berlin:Springer,1986. [5] GUTMAN I,CYVIN S J.Introduction to the Theory of Benzenoid Hydrocarbons[M].Berlin:Springer,1989. [6] WAGNER S,GUTMAN I.Maxima and minima of the Hosoya Index and the Merrifield-Simmons index[J].Acta Appl Math.2010,112:323-346. [7] 曹月芬,张福基.基于k-匹配的极值五角链[J].厦门大学学报:自然科学版,2008,47(4):471- 474. Hosoya Index of Pentagon Chains TIANWen-wen1,YANGFei2,TIANShuang-liang1 (1.School of Mathematics and Computer Science, Northwest University for Nationalities, Lanzhou 730030, China;2. China Minorities Information Technology Institute, Northwest University for Nationalities, Lanzhou 730030, China) Hosoya index is one of the popular important topological indexes in the study of Chemistry molecular graph theory. This paper studies Hosoya index under different isomorphically connected positions of pentagon chains and gives more general computation formula. pentagon chain;Hosoya index;computation formula 1672-058X(2013)09-0029-05 2013-04-17; 2013-05-17. 国家自然科学基金资助项目(11161041);西北民族大学中央高校科研专项资金资助研究生项目(ycx13160);中央高校基本科研业务费专项资金项目(zyz2012077). 田文文(1987-),男,甘肃天水人,硕士生,从事图论与组合优化研究. O157.5 A 责任编辑:代小红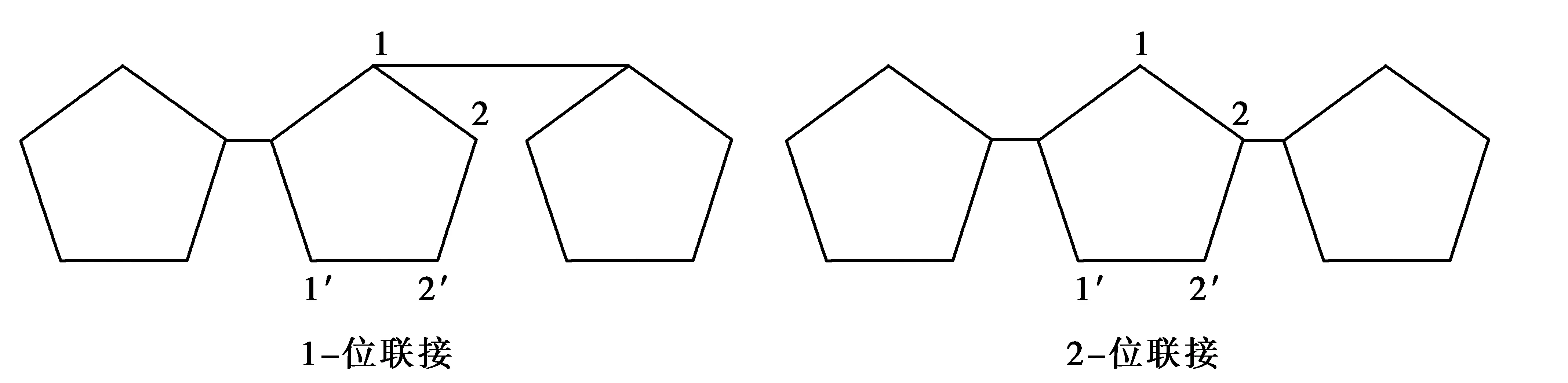
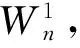


1 主要结论及其证明
3 进一步的结果