带负顾客的M/G/1重试可修排队系统*

高显彩， 宋 杨， 张丽慧

(1.宿州学院 数学与统计学院，安徽 宿州 234000；2.宿州市第二中学，安徽 宿州 234000)

带负顾客的M/G/1重试可修排队系统*

高显彩1， 宋 杨1， 张丽慧2

(1.宿州学院 数学与统计学院，安徽 宿州 234000；2.宿州市第二中学，安徽 宿州 234000)

基于互联通讯网性能研究的需要，提出了带负顾客的M/G/1重试可修排队系统；其中负顾客的机制是带走正在接受服务的正顾客和使得服务器处于修理状态；在假定重试区域中只有队首的顾客允许重试的情况下，重试时间具有一般分布时，得到了系统稳态的充分必要条件；求得了系统稳态时队长和重试区域中队长分布及一些排队指标和可靠性指标。

负顾客；重试排队；概率母函数

Gelenbe[1]在1991年提出了负顾客的排队模型，从而开创了负顾客排队模型的先河。随后Harrision和Pitel[2]、Bayer和Boxma[3]、Zhu Yijun[4]等对负顾客排队模型都作了大量研究。目前，负顾客已渗透到交通、机械、控制以及计算机等许多领域。重试排队系统的特征就是当顾客到达时发现服务台忙，则必须离开服务区域，经过一段时间后再次要求服务，在相连两次要求服务的时间内顾客处在重试区域中。可修的重试排队系统已经有学者研究过[5-9]，但还没有把负顾客和可修重试排队系统相结合来进行研究，本文研究了带负顾客的M/G/1重试可修排队系统，服务器的故障由负顾客引起，这样的模型更适合于对通讯网络中的噪音、信号干扰现象、计算机网络中的病毒干扰现象的研究。

1 模型描述

正、负顾客到达过程服从参数为λ+、λ-的Poisson流。正顾客(包括新到达的和重试的)到达系统时，若发现服务器空闲，则立刻接受服务，服务结束后以概率θ离开系统，以概率1-θ进入重试区域中；若服务器处于工作或修理状态则进入orbit中，不断进行重试，直到重试成功。假定重试区域的容量为，按照FCFS规则，只有队首的顾客允许重试，相继重试时间间隔服从一般分布函数A(x)，其密度函数a(x)，风险率函数为r(x)，γ*(x)表示其拉普拉斯司梯阶变换(LST)。负顾客到达系统时，若系统处于工作状态，它使系统马上进入修理状态后立即消失，同时带走正在接受服务的正顾客；若系统处于闲期或修理状态，负顾客自动消失。不会对系统造成任何影响。

单服务器，服务时间的分布函数为B(x)，密度函数为b(x)，风险率函数为μ(x)，以B*(x)表示其拉普拉斯司梯阶变换(LST)。修理时间的分布函数为G(y)，密度函数为g(y)，风险率函数为β(y)，有有限的一阶矩g1和二阶矩g2，以G*(y)表示其拉普拉斯司梯阶变换(LST)。顾客的到达过程、重试时间间隔、修理时间间隔、服务时间间隔均相互独立。当服务台处于空闲状态时，新到达的顾客与重试区域中的顾客(若有)按到达服务台时间的先后接受服务。

系统在任意时刻的状态可用马尔可夫过程{C(t)，X(t)，ξ0(t)，ξ1(t)，ξ2(t)；t≥0}表示，其中C(t)表示时刻t服务台所处的状态(取值0，1，2，分别表示服务台处于空闲状态，工作状态，修理状态)，X(t)表示时刻t重试组中的顾客数，当C(t)=0时，ξ0(t)表示在时刻t逝去的重试时间，当C(t)=1时，ξ1(t)表示在时刻t逝去的服务时间，C(t)=2时，ξ2(t)表示在时刻t逝去的修理时间。

系统达到稳态的充要条件：λ-(1-θ)B*(λ-)+λ+(1+λ-g1)(1-B*(λ-))<λ-γ*(λ+)。

2 模型方程的建立与求解(图1)

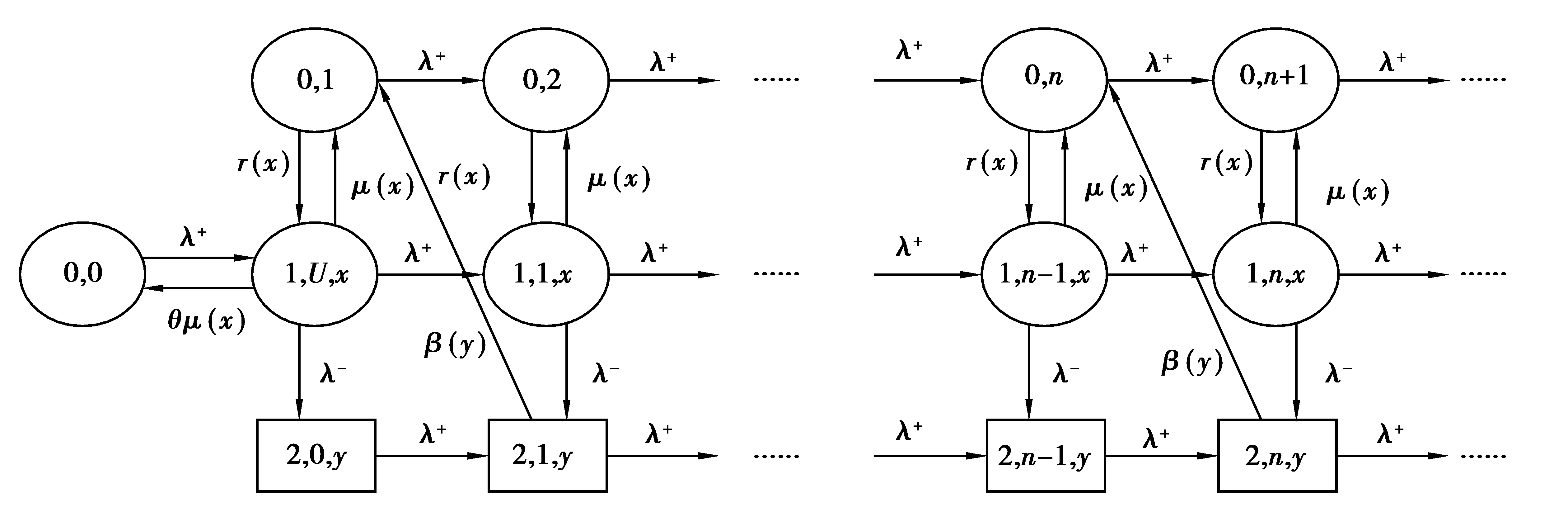
图1 带负顾客的M/G/1重试可修排队系统的状态转移图

令P0(t)=P{C(t)=0，X(t)=0}，Pn(x，t)dx=P{C(t)=0，X(t)=n，x≤ξ0(t)≤x+dx}，t≥0，x≥0，n≥1Qn(x，t)dx=P{C(t)=1，X(t)=n，x≤ξ1(t)≤x+dx}，t≥0，x≥0，n≥0。Rn(y，t)dy=P{C(t)=2，X(t)=n，y≤ξ2(t)≤y+dy}，t≥0，y≥0，n≥0。

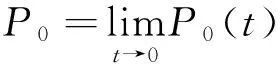
边界条件：

正则性条件：

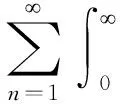
(11)

对微分式(1)-式(10)经过计算可得：

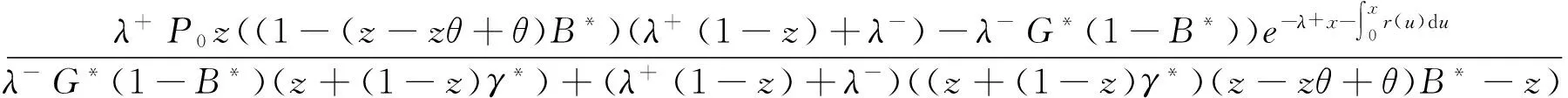
(12)

其中

在式(15)-式(17)中令z=1运用L′Hospital法则并由正则性条件有P0+P(1)+Q(1)+R(1)=1，经过整理可得：

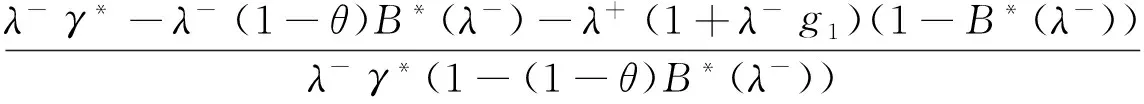
(18)

令H(z)=P0+P(z)+Q(z)+R(z)，则H(z)为重试区域中顾客数的概率母函数：

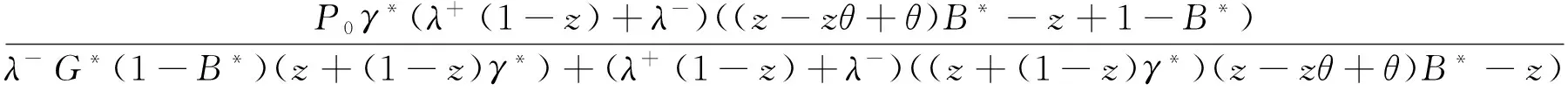
令K(z)=P0+P(z)+zQ(z)+zR(z)，则K(z)为稳态时系统中的顾客数的概率母函数：

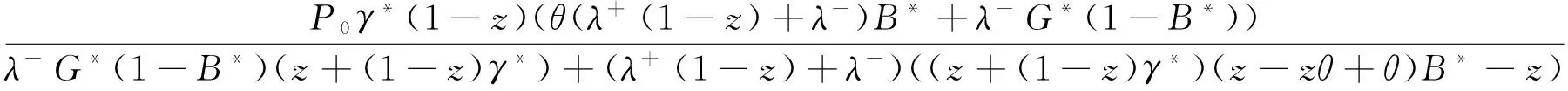
3 相关指标

令PI表示重试期间服务台处于空闲状态的概率，PQ表示服务台处于工作状态的概率，PR表示服务台处于修理状态的概率，PE表示重试区域为空的概率，则有：

令WS表示系统稳态时顾客的平均等待时间，则由Little公式得：WS=Ls/λ+.Wq表示系统稳态时重试区域中顾客的平均等待时间，则Wq=Lq/λ+.

4 结 论

研究了带负顾客的M/G/1重试可修排队系统，利用补充变量的方法求得了稳态时系统的队长、重试区域中的队长、以及服务台处于忙和闲的概率。关于负顾客的排队模型有待于进一步研究。

[1] GELENBE E P. Queues with negative arrivals [J].J Appl Prob，1991(28)：245-250

[2] HARRISON P. The M/G/1 queue with negative customers[J].A Appl Prob，1996(28):540-566

[3] BAYER B，WIENER H. Analysis of an M/G/1 queue with negative customers and of a related class of random walks [J].Queueing Systems，1996(23)：301-316.

[4] ZHU Y. Analysis on a type of M/G/1 models with negative arrivals[A]. In： Proceeding of the 27th stochastic process conference [C].UK，July 2001.

[5] WANG J T，CAO J H. Reliability analysis of the retrial queue with server breakdowns and repairs[J]. Queuing Systems，2001，38(4)：363-380

[6] 伍慧玲，尹小玲.有单移除策略的M/G/1重试可修排队系统[J].中山大学学报：自然科学版，2005，44(21)：133-137

[7] 朱翼隽，童仁群，王晓春，等.有可选到达、服务台可修的M/G/1重试可修排队系统[J].江苏大学：自然科学版，2007，28(1)：85-88

[8] 朱翼隽，周宗好.冯艳刚具有优先权的M/G/1重试可修排队系统[J].自动化学报，2008，34(2)：195-201

[9] 周宗好，朱翼隽.冯艳刚具有Bernoulli休假的M/G/1重试可修排队系统[J].运筹学学报，2008，12(1)：71-82

M/G/1 Retrial Queuing System with Negative Customers and Repairs

GAOXian-cai1,SONGYang1,ZHANGLi-hui2

(1.School of Mathematics and Statistics, Suzhou University, Anhui Suzhou 234000, China；2. No.2 Middle School of Suzhou City, Anhui Suzhou 234000, China)

Based on the demand of internet communication performance, this paper proposes M/G/1 retrial queuing system with negative customers and repairs, in which the mechanism of negative customers is to take away the positive customers who are enjoying service and to make the server stay in repair state, in the supposed retrial region, under the condition that only the customers at the queuing head are allowed to conduct retrial, if retrial time has general distribution, the sufficient and necessary condition for the system stability is obtained, the queuing length in the stable state of the system, the distribution of queuing length in retrial regions, some queuing indexes and reliability indexes are

.

negative customer；retrial queuing；probability generating function

1672-058X(2013)09-0065-05

2013-03-14；

2013-04-20.

安徽高等学校省级自然科学研究项目(KJ2011B178).

高显彩(1983-)，男，安徽界首人，助教，从事排队论研究.

TP235

A

责任编辑：代小红