具有时滞的SIQR计算机病毒模型分析

杨 斌

(重庆师范大学 数学学院，重庆 401331)

具有时滞的SIQR计算机病毒模型分析

杨 斌

(重庆师范大学 数学学院，重庆 401331)

通过分析已有的计算机病毒在网络传播过程中的动力学行为，参照了生物学中传染病学的数学模型，结合计算机自身的实际特性，考虑计算机病毒的潜伏状况以及计算机的杀毒软件的使用；同时引入离散时滞，建立了描述具有时滞隔离项SIQR的计算机病毒动力学模型；利用微分方程理论对该模型进行分析；得到了计算机病毒能否被控制取决于阈值R0，当R0<1时，系统无病平衡点是全局吸引的；当R0>1时，讨论了系统的持续性。

计算机病毒；SIQR模型；持续性

国内外大量的学者对计算机病毒的传播作了研究[1- 4]。Kephart等人在1991年第一次引入传染病数学模型对计算机病毒模型进行初步分析[1]，许多学者在此基础上不断加以改善和研究。最近主要成果有xiehan等人引入时滞建立了具有潜伏性时滞的SIRS的病毒模型[2]，冯丽萍等人提出了具有安装的反病毒软件模式的SIR的模型[3]，Misha和Navint Jha提出具有隔离项的垂直传播的SEIQRS计算机病毒传播模型[4]等。本文在以上文献基础上，参照了生物学中传染病学的数学模型[5]，考虑了现实网络中节点数量的变化以及加入离散时滞τ，结合了计算机病毒在网络中传播的实际特性，建立了具有时滞隔离项的SIQR计算机病毒传播模型。

1 模型的建立

假设网络中一台计算机主机或路由器看作一个节点。则某t时刻，节点可能处于以下4个状态之一，以S(t)表示t时刻节点未被感染但容易被感染的易感染节点数；I(t)表示t时刻节点已被感染的且具有传染性的感染节点数；Q(t)表示t时刻已感染的节点并通过某种人为的或者杀毒软件自身对病毒文件进行了隔离的隔离节点数；R(t)表示t时刻通过病毒查杀或重装系统获得对病毒免疫状态的免疫节点数。为了简便，这里假设节点一旦进入R(t)状态则不具备传染性。

图1为SIQR模型中节点的状态迁移图。其中b表示新增的节点数，β表示易感染节点与感染节点的传染率系数，ρ为新增节点数中系统装有防火墙或者装有主动防御病毒软件而直接进入免于状态的概率。d表示节点自然死亡的概率，δ表示病毒被人为隔离或系统软件主动将病毒文件隔离的概率，γ表示反病毒软件将病毒查杀或重装系统进入免于状态的概率，ε表示病毒在隔离区被查杀进入免疫状态的概率，α1、α2分别表示已感染节点、被隔离节点因病毒导致死亡的概率。τ表示病毒感染节点后到病毒被激活所潜伏的时间。

图1 病毒模型状态迁移图

根据上述假设及传播动力学理论，建立如下SIQR模型：

(1)

设某时刻t，节点总数为N(t)，则S(t)，I(t)，Q(t)，R(t)满足：

N(t)=S(t)+I(t)+Q(t)+R(t)

进一步假设式(1)的初始条件：S(t)≥0，S(0)>0;I(t)≥0，I(0)>0;Q(t)≥0，Q(0)>0;R(t)≥0，R(0)>0。将式(1)的各个方程相加，得到：

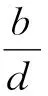
引理1 若式(1)的解存在，则所有解均为正。

证：首先证I(t)为正.

故得：I(t)≥I(0)exp(-(δ+d+α1+λ)t)>0。

同理易证S(t)>0 ，I(t)>0，Q(t)>0，R(t)>0。

证毕。

由上述结果，可以得到式(1)的可行域：

由于式(1)前两个方程不含有变量Q，R.因此只需要考虑系统：

(2)

2 模型分析

2.1 无病平衡点

V′=βS(t)I(t)-(δ+d+α1+γ)I(t)=I(t)[βS-(δ+d+α1+γ)]≤0

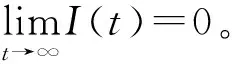
证毕。

2.2 地方病平衡点

引理2[6]考虑方程x′(t)=ax(t-τ)-bx(t)，当a，b，τ>0时，且x(t)>0，-τ≤t≤0，然后有：

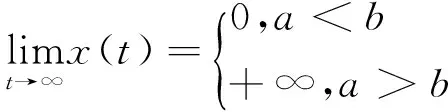
定理2 当R0>1时，式(2)是持续的。

3 模型仿真

为了验证上述结果的正确性，对式(2)进行数值仿真，并对仿真的结果进行了分析，如下：

(2) 取p=0.5，b=1，β=0.1，d=0.01，δ=0.1，α1=0.01，γ=0.5，τ=1。此时，计算R0得出R0=8.0645>1，根据定理2，得到式(2)是持续存在的，如图3所示。

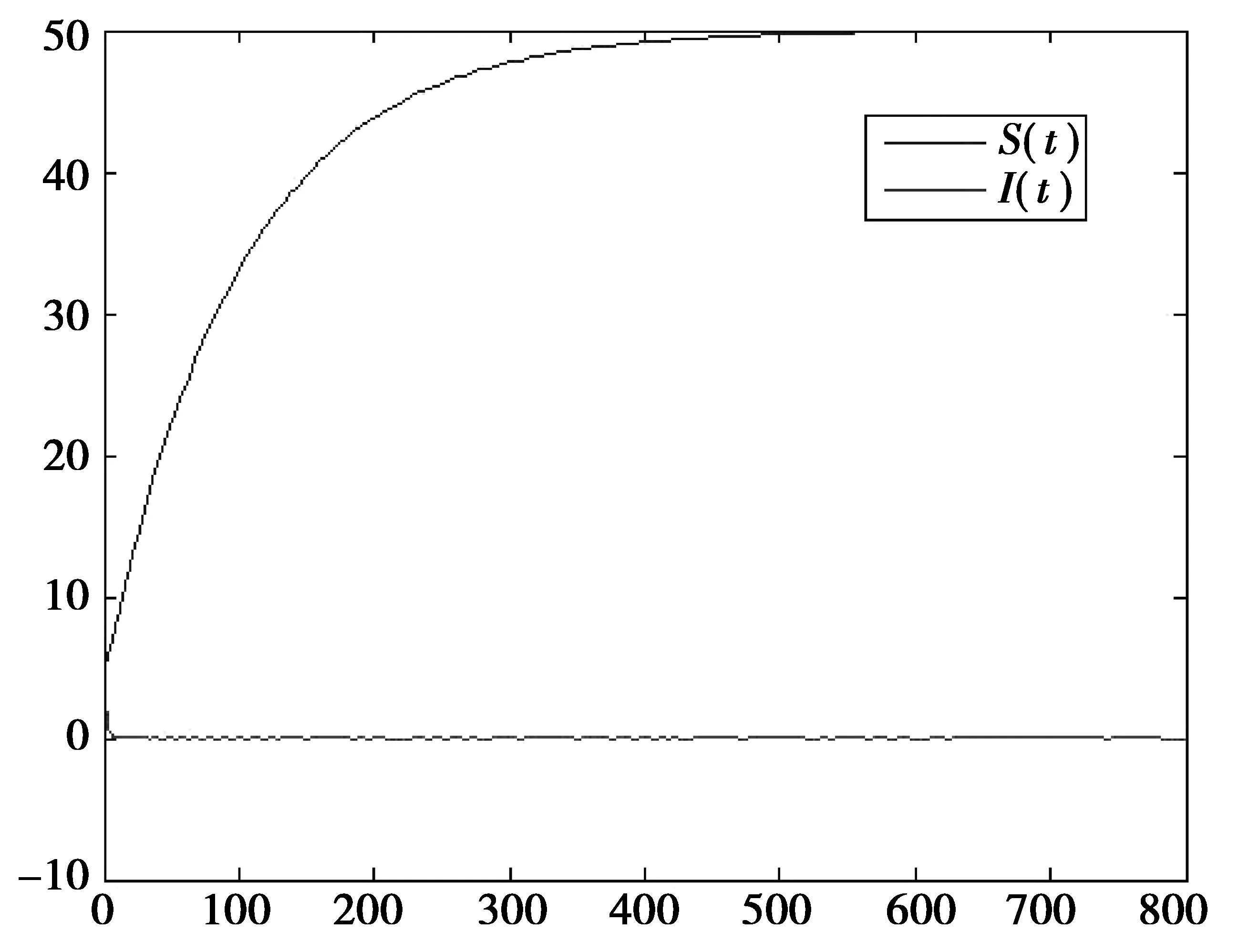
图2 R0<1时，无病平衡点数值仿真

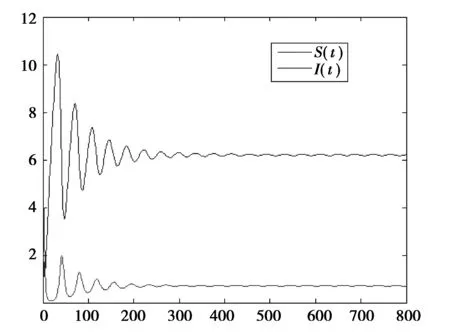
图3 R0>1时，数值仿真的持续状态

4 结束语

基于经典的计算机病毒模型基础上建立了一个具有时滞隔离项SIQR计算机病毒模型，同时分析了该模型的动力学行为，发现该模型动力学行为取决于阈值R0.当R0<1时，式(2)的解是吸引的；当R0>1时，式(2)是持续存在的。因此，为有效的控制和消除计算机病毒在网络上的传播，应尽量减少R0的值。

[1] KEPHART J O， WHITE S R. Directed graph epidemiological model of computer viruses [C] / / Proceedings of the 1991 IEEE Symposium on Security and Privacy. Washington DC: IEEE Computer Society，1991: 343 - 359

[2] HAN X，TAN Q. Dynamical behavior of computer virus on Internet[D]. Appl. Math. Comput，2010(217)：2520-2526

[3] 冯丽萍，王鸿斌，冯素琴.改进的SIR计算机病毒传播模型[J].计算机应用，2011，31(7):1891-1893

[4] BIMAL K，NAVNIT J. SEIQRS model for the transmission of malicious objects in computer network[J].Applied Mathematical Modelling，2010(34)：710-715

[5] 万维明，徐婧.具有时滞隔离项的SIQR传染病模型的稳定性分析[J].大连交通大学学报，2011，32(4):99-102

Analysis of SIQR Computer Virus Model with Time Delay

YANGBin

(School of Mathematics, Chongqing Normal University, Chongqing 401331, China)

By analyzing the dynamics behaviors of existed computer viruses in the process of network transmission and by comparing with mathematical model of infectious diseases in biology, the latent condition of computer viruses and application of computer antivirus software are considered based on the actual characteristics of a computer, meanwhile, discrete time-delay is introduced and computer virus dynamics model with the description of time-delay isolation item SIQR is set up. The analysis of this model by using differential equation theory obtains whether computer viruses can be controlled depends on threshold valueR0, whenR0<1, the virus-free equilibrium point of the system is globally attractive, whenR0>1, the sustainability of the system is discussed.

computer virus；SIQR Model；sustainability

1672-058X(2013)09-0070-04

2013-03-03；

2013-04-20.

杨斌(1987-)，男，研究生，从事系统分析与控制研究.

O175.1

A

责任编辑：代小红