基于序列重要性重采样算法的MIMO时变信道半盲估计

石丹凤，张 静

(上海师范大学信息与机电工程学院，上海200234)

0 引言

随着多媒体宽带业务的不断增加，未来无线通信系统对传输速率、误码率和频谱利用率等系统性能提出了更高的要求．多输入多输出(MIMO)通信系统与单天线通信系统相比，具有成倍增长的信道容量和频谱利用率，所以MIMO通信系统技术的研究与应用有了巨大的意义．在无线通信系统中，时变信道估计的好坏直接影响接收端的相关检测性能．较为经典的时变信道盲/半盲估计方法主要有:最小均方(LMS)算法、递推最小二乘(RLS)算法和卡尔曼(Kalman)滤波算法，而卡尔曼滤波算法的估计性能要好于其他2种算法［1］．然而卡尔曼滤波对环境噪声的鲁棒性较差，无法适用于非高斯环境噪声．粒子滤波是一种基于蒙特卡罗仿真思想和递推贝叶斯估计的滤波方法，经过多年的发展已成为解决非线性、非高斯动态系统的参数估计和状态滤波问题的主流方法．然而粒子滤波存在粒子退化问题，为改善粒子退化问题，可以增加采样粒子数，但实时性较差．解决该问题的最有效的方法是选择好的重要性概率密度函数和采用重采样方法［2］．序列重要性重采样算法通过对重要性函数重采样，减少权值较小的粒子数目，复制具有较大权值的粒子上，在一定程度上解决了粒子的退化问题．所以可以运用序列重要性重采样算法对MIMO时变信道进行半盲估计．

首先对MIMO无线通信系统及时变信道模型进行阐述，然后在此基础上介绍基于序列重要性重采样的MIMO时变信道半盲估计．并将传统的序列重要性重采样算法包括多项式重采样算法、分层重采样算法、系统重采样算法、剩余重采样算法［3－4］应用于非线性、非高斯系统模型，对算法的估计精度、计算复杂度和抑制粒子退化的程度进行了仿真比较，结果表明系统重要性重采样算法的估计精度相对较高，且计算复杂度最低．之后，在此基础上运用系统重采样算法来进行MIMO时变信道半盲估计，与传统的粒子滤波算法相比，均方误差和误码率更低，从而改善了接收端的符号检测性能．

1 MIMO无线通信系统及时变信道模型

1．1 系统模型

考虑一个具有Nt根发射天线和Nr根接收天线的MIMO无线通信系统，并做如下假设:

(1)系统每对收发天线间的多径信道互不相关，且多径数目相同;

(2)每对收发天线间的信道满足抽头延迟线(TDL)模型;

(3)系统接收端处各接收天线上的加性噪声互不相关;

(4)系统接收端已实现理想同步;

(5)循环前缀(CP)长度大于信道最大长度．

假设在时刻n，系统发射端经BPSK调制后再经过空时编码处理得到了第i根发射天线上的信息序列为{Sin:i=1，2，…，Nt}，第 i根发射天线与第 j根接收天线之间的信道频率响应为{Xj，in，i=1，2，…，Nt;j=1，2，…，Nr}，第j根接收天线上的加性噪声频率响应为vjn．于是在n时刻，频域等效基带接收信号可以表示为

其中，T表示矩阵转置，不失一般性，仅考虑第j跟接收天线上接收信号的频域表达式为

写成矢量形式为

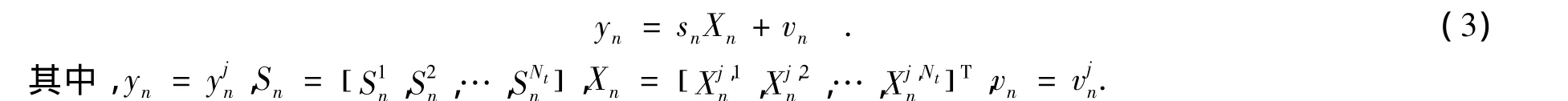
对于噪声vn，考虑Middleton－A类噪声模型，它通常被用来建模室内或郊区无线通信环境下普遍产生的噪声冲击响应［5］．其概率密度函数为

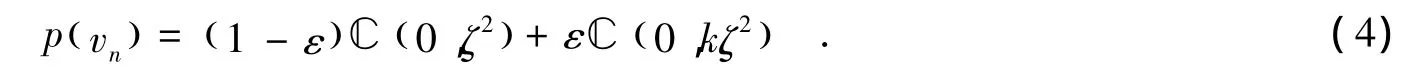
其中，0≤ε≤1，k≫1，C 0，ζ()2表示背景噪声分量，为均值为0、方差为ζ2的复高斯分布;C 0，kζ()2为均值为0、方差为kζ2的复高斯分布，表示脉冲噪声分量，以概率ε出现．

1．2 时变信道状态模型

可以将信道建模为一阶自回归(AR)模型［6］，在时刻n+1，第i根发射天线与第j根接收天线间的信道频率响应Xj，in+1可以表示为

其中，a为AR模型系数，反应时变信道变化快慢，dj，in为AR模型动态驱动噪声，均值为0、方差为可以通过(6)、(7)两式求得系数a和σ2v．

其中，J0()·表示一阶Bessel函数，fdTs为信道归一化多普勒衰减率．将(5)式写成矩阵形式

其中，A为Nt×Nr对角阵，对角元素为a;dn为Nt×1噪声矢量，

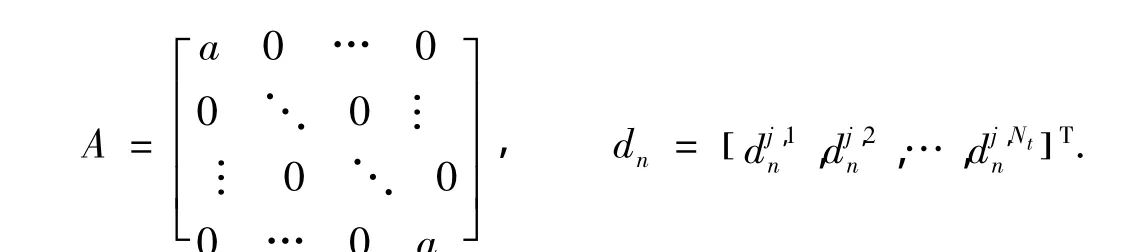
根据(3)和(8)式，构建MIMO时变信道状态空间模型如下:

2 序列重要性重采样算法

对于非线性、非高斯过程，其状态空间模型［6］可表示为

式(11)、(12)中，f和h为有界非线性映射，xk和zk分别是状态向量和观测向量，vk和nk分别为过程噪声和量测噪声，它们相互独立，且协方差分别为Qk和Rk的零均值加性噪声．

在序列重要性重采样算法中，首先初始化粒子，从重要性密度函数中采样得到一组随机样本粒子，计算权值并归一化，然后进行重采样，不断调整粒子的权重和位置，递推估计出状态后验概率分布．序列重要性重采样算法的具体过程［7］如下:

(1)初始化:由先验概率p(x0)产生N个粒子的集合{xi0}Ni=0，各粒子权值为1/N．

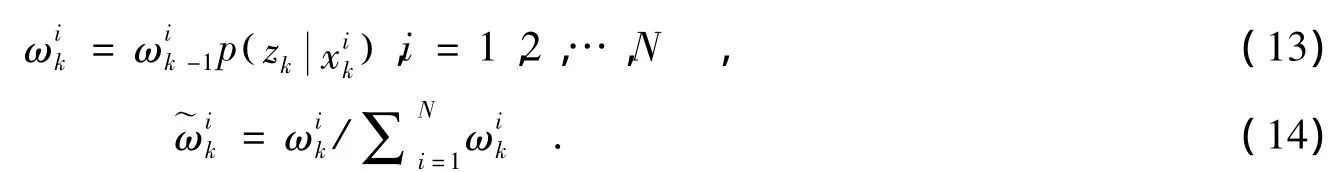
则可得到k时刻状态向量x的最小均方估计为

(4)在下一时刻k=k+1，利用状态方程预测状态向量xik+1，重复第2、3、4 步．

在序列重要性重采样步骤中可使用不同的重采样方法，目前，重采样算法包括多项式重采样算法、分层重采样算法、系统重采样算法、剩余重采样算法4种［3－4］．多项式重采样算法是各种重采样算法的基础，它在(0，1］区间产生N个有序的均匀分布随机数，并计算归一化权值的累计分布函数，观察之前产生的均匀分布随机数落在累计分布函数的哪一区间，然后选择复制该区间所代表的粒子．分层重采样算法利用了分层统计的思想对多项式重采样算法进行了改进，将(0，1］分成N个连续的互不重合的区间，对每个区间独立同分布采样得到有序的样本集合．系统重采样算法同分层重采样算法一样，将区间(0，1］分成N层，不同的是样本在每层中的位置相同．因此产生的随机样本不再独立，而是把它们之间的差别降到最小．剩余重采样算法以多项式重采样算法为基础，对归一化权值的累积分布函数的每一区间进行取整运算，剩余部分组合成一个新的累积分布函数，再利用之前所述的3种重采样算法中的1种进行采样．

3 基于序列重要性重采样算法的MIMO时变信道半盲估计

MIMO时变信道状态空间模型如式(9)和(10)所示，利用序列重要性重采样算法对MIMO时变信道进行半盲估计，主要由训练阶段和时变信道估计阶段两部分组成．首先，系统发射端发送1个接收端已知的训练序列，接收端则利用训练序列完成初始信道估计;在下一时刻，接收端再根据初始信道估计值，用序列重要性重采样算法对当前时刻的信道状态进行估计，得到当前时刻的信道状态，利用它来解码得到发射端发射的信息．

MIMO无线通信系统的联合估计原理框图如图1所示［8］，二进制源信息经过8－PSK调制后再进行空时编码处理，编码后的信息序列Sn经无线信道传输，被信道频率响应矩阵Xn所影响．在接收端，空时解码过程外设一个估计循环路径．刚开始时，预测器将经训练阶段产生的信道频率响应状态估计更新为当前时刻的状态估计，预测粒子的均值被送入空时解码过程，加上当前时刻的接收信号yn产生发送信号Sn的粗糙估计，滤波器则利用运用序列重要性重采样算法来估计产生新的状态估计粒子最后利用这个新的状态估计粒子获得更准确的信道状态估计，和yn一起送入空时解码过程得到最终的发送信号估计值．与此同时经时间延迟τ送入下一时刻n+1的预测器并开始新一轮的信道估计．整个估计过程中，接收端只在训练阶段需要训练序列或导频信息，在后续的时变信道估计阶段不再需要发射序列信息，所以相对基于训练序列或导频的信道估计而言，提高了无线通信系统的频谱利用率．而与盲信道估计相比较则计算复杂度降低．

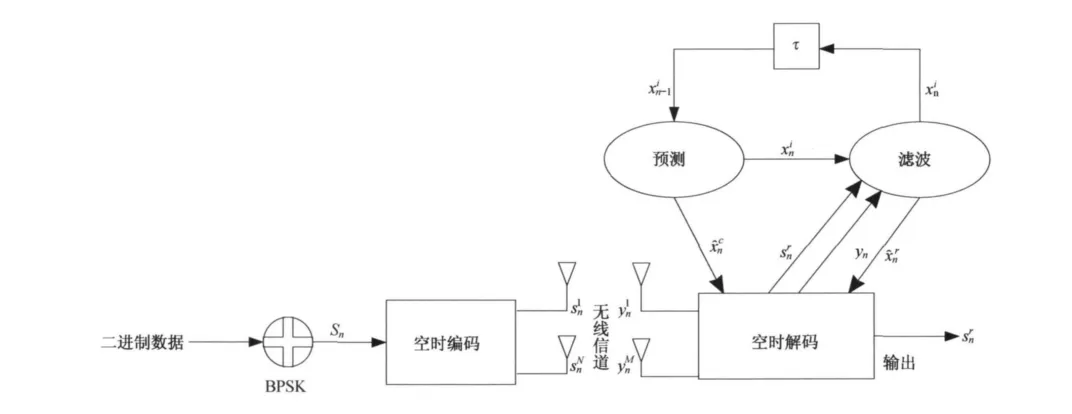
图1 MIMO无线通信系统的联合估计原理框图

4 仿真实验结果与讨论

4．1 4种序列重要性重采样仿真比较

下面将通过仿真实验来比较这4种序列重要性重采样算法的估计精度，以及算法的计算复杂度和抑制粒子退化程度．实验采用单变量静态增长模型(UNGM模型)，仿真对象的过程噪声和量测噪声如下［9］．

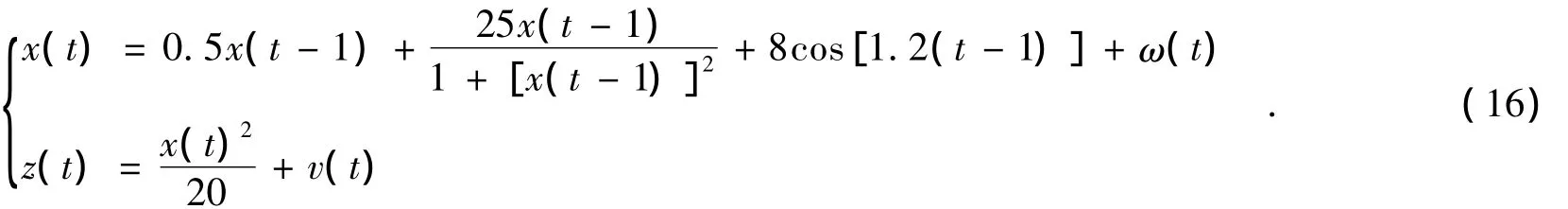
式(16)中，ω(t)和v(t)为零均值高斯噪声．

分别采用4种序列重要性重采样算法来进行状态估计和跟踪．均方根误差公式为

为精确比较这4种序列重要性重采样算法的估计精度，图2给出了它们的均方根误差曲线．仿真取Q=0．25、R=0．4，不同的粒子数下将算法运算1 000次取均方误差(RMSE)的平均值绘制而成．由图2可知，4种序列重要性重采样算法的均方误差估计相近，但仍可看出系统重要性重采样算法的均方误差估计相对较小，说明系统重要性重采样算法的估计精度相对较高．

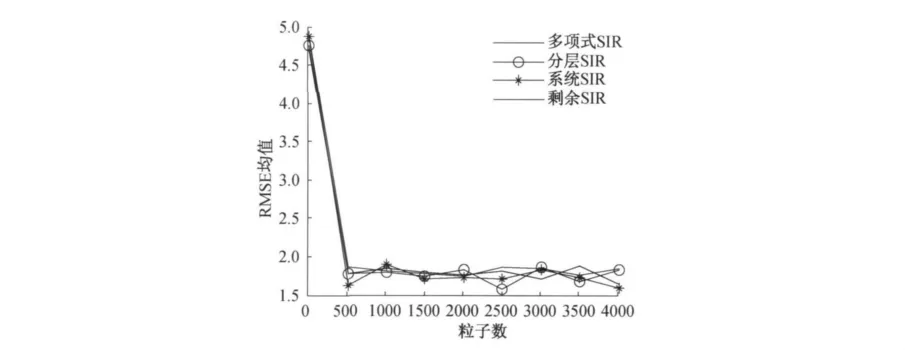
图2 4种序列重要性重采样算法的均方根误差曲线

算法的计算复杂度可以由算法运行时间来衡量，在仿真中，取 Q=0．25、R=0．4，重要性重采样算法的运行时间取1 000次独立实验的平均运行时间．4种序列重要性重采样算法的运行时间和粒子数目之间的关系图如图3所示．由图3可知，4种序列重要性重采样算法的运行时间和粒子数目基本上呈线性增长关系，系统重采样算法和分层重采样算法的运行时间相近，比其余2种重采样算法运行时间短．

同时，为考察算法的粒子退化程度，分别选取如表1中所示3种情况，将算法运行500次，计算每种算法迭代100步后有效样本数的平均值，得到如表1所示的仿真结果．由表1可以看到3种情况下，4种序列重要性重采样算法的有效样本数都很相近，表明这4种序列重要性重采样算法抑制粒子退化程度的效果相似．

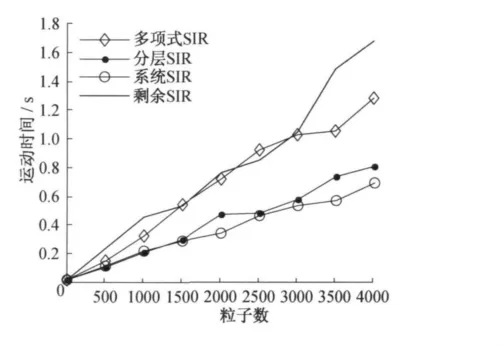
图3 4种序列重要性重采样算法运行时间和粒子数目关系

表1 4种序列重要性重采样算法的有效样本数比较

实验结果表明，4种序列重要性重采样算法的非线性状态估计精度相近，抑制粒子退化程度相近．但系统重要性重采样算法的估计精度相对较高，计算复杂度最低．

4．2 MIMO时变信道半盲估计

考虑上一部分实验结果，在4种重采样算法中，系统重要性重采样算法的估计精度相对较高，计算复杂度最低，所以在以下的仿真实验中，采用系统重要性重采样算法来对MIMO时变信道进行半盲估计，并与使用传统的粒子滤波算法进行比较．实验环境是具有2根发射天线和2根接收天线2×2的MIMO无线通信系统，系统工作在2．4 GHz的载频上，带宽为10 MHz，二进制源信息经8－PSK调制后送入空时编码，采用广义平稳非相关散射信道，归一化多普勒衰减率为0．05．干扰噪声假设为Middleton－A类噪声模型，取ε=0．25，k=100．在信噪比(SNR)从0 dB到30 dB的不同环境下，对系统重要性重采样算法和传统粒子滤波的信道估计性能进行了比较．共进行100次Monte Carlo实验，采样粒子数为100．

4．2．1 归一化均方误差比较

当环境噪声为Middleton－A类噪声模型时，系统重要性重采样算法和传统粒子滤波估计算法的均方误差性能比较如图4所示．由图4可知，基于系统重要性重采样算法的MIMO时变信道估计与使用传统粒子滤波算法相比，归一化均方误差性能更好．

4．2．2 误码率比较

当环境噪声为Middleton－A类噪声模型时，系统重要性重采样算法和传统粒子滤波估计算法的(SER)性能比较如图5所示．采用系统重要性重采样算法进行MIMO时变信道半盲估计时，系统接收端的SER性能明显好于粒子滤波估计方法，且采用基于系统重要性重采样算法的MIMO时变信道半盲估计方法的SER性能曲线更接近于理想信道估计(Perfect SCI)的SER曲线．

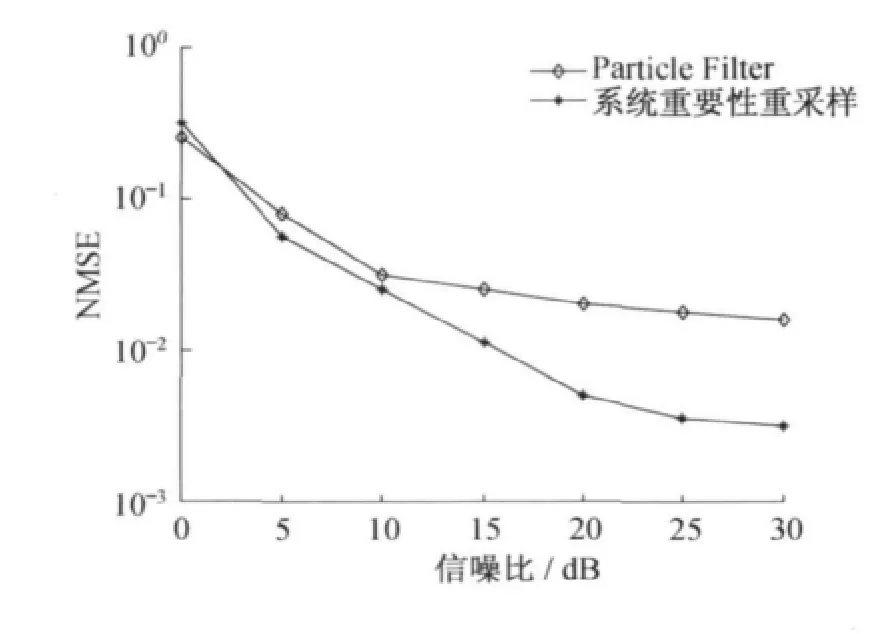
图4 MIMO时变信道半盲估计的归一化均方误差比较

图5 MIMO时变信道半盲估计的误符号率(SER)比较

5 结束语

本文作者对基于序列重要性重采样算法的MIMO时变信道半盲估计方法进行了阐述，并对4种序列重要性重采样算法进行了比较，结果系统重要性重采样算法的估计精度相对较高，计算复杂度最低．最后通过实验仿真比较了系统重要性重采样算法和传统粒子滤波的MIMO时变信道半盲估计性能．结果表明，与传统粒子滤波估计方法相比，基于系统重要性重采样算法的MIMO时变信道半盲估计方法的均方误差和误码率性能都较好，从而有效提高了MIMO无线通信系统接收端的检测性能．

［1］HAYKIN S，SAYED A H，ZEIDLER J R．Adaptive tracking of linear time－variant systems by extended RLS algorithms［J］．IEEE Transactions on Signal Processing，1997，45(5):1118 －1128．

［2］ARULAMPLAM S，MASKELL S，GORDON N，et al．A tutorial on particle filters for on－line non－linear/non－Gaussian Bayesian tracking［J］．IEEE Trans Signal Process，2002，50(2):174－188．

［3］DOUCR，CAPPÉ O，MOULINESE．Comparison of resampling schemes for particle filtering［C］．Istanbul:Proceedings of 4th international Symposium，ISPA，2005．

［4］付何伟，金明录，崔承毅．粒子滤波重采样及在盲均衡中的应用［J］．通信技术，2010，43(7):25－30．

［5］MIDDLETON D．Non－Gaussian noise models in signal processing for telecommunications:new methods and results for class A and class B noise models［J］．IEEE Transactions on Information Theory，1999，45(4):1122 －1129．

［6］WANG H，CHANG P．On verifying the first－order Markovian assumption for a Rayleigh fading channel model［J］．IEEE Transactions on Communications，1996，45(2):353 －357．

［7］LI T C，SATTAR T P，SUN SD．Deterministic resampling:Unbiased sampling to avoid sample impoverishment in particle filters［J］．Signal Processing，2012，92(7):1637 －1645．

［8］HAYKIN S，HUBER K，CHEN Z．Bayesian sequential state estimation for MIMO wireless communications［J］．Proceedings of the IEEE，2004，92(3):439－454．

［9］SCHÖN T B，WILLSA，NINNESSB．System identification of nonlinear state－space models［J］．Automatica，2011，47(1):39－49．