钢筋混凝土双柱桥墩抗震能力Pushover分析

王红伟，刘建新

(上海师范大学建筑工程学院，上海201418)

0 引言

对于桥梁结构抗震分析主要是对墩柱抗震性能的研究．目前常用的方法包括线弹性反应谱法、弹塑性动力时程分析法、等效静力分析法等．线弹性反应谱法由于难以正确反映结构开裂后的非弹性阶段的特性，其应用范围受到一定限制;弹塑性时程分析方法由于需要准备包括场地地震波等在内的大量数据，且其计算繁琐，难以在实际工程应用中广泛推广;等效静力分析方法由于其计算过程简单、实用，因而在桥梁抗震分析中已得到广泛应用．Pushover方法则是应用最多的等效静力分析方法．

对Pushover分析研究较多的是欧美学者，早在1975年Freeman等［1］提出了一种简单实用又比较可靠的抗震设计方法——静力弹塑性分析方法(Pushover分析方法)，以后虽有一定的发展，但未引起更多的重视．20世纪90年代以后，随着基于性能的抗震设计思想的提出和发展，Pushover分析方法引起了地震工程界的广泛兴趣［2］．1998年，Helmut Krawinkler对静力弹塑性分析方法作了更为全面的阐述，论述了Pushover方法的优点、适用范围，并指出了其局限性所在，给Pushover方法的研究工作做了恰当的定位，对研究静力弹塑性分析方法具有较高的理论价值［3］．1999年，Chopra等利用R－μ关系对弹性反应谱进行折减，并转化成非弹性需求谱的形式，提出了改进的能力谱方法，大大提高了能力谱方法的计算精度［4］．

近年来，国内学者对Pushover分析方法也纷纷展开了研究，作为一种简单而有效的结构抗震能力评价工具，Pushover分析方法已经在我国得到了普遍推广．孙景江对各种荷载分布模式得到的结构能力曲线进行了对比研究，并且提出了改进的分布模式［5］．巍巍和冯启民对能力谱方法、位移影响系数法和适应谱Pushover方法进行了详细的对比研究，指出了其中存在的问题［6］．王亚勇等将非线性静力分析方法用空间结构，采用空间弹塑性推覆模型，对泉州邮电综合大楼进行了地震非线性静力分析计算［7］．叶献国和李康宁等通过算例分析说明了在对非对称结构进行Pushover分析时，对两个相反方向加载的结果有所不同，并且提出了往复循环加载方式［8］．Pushover分析方法相对时程分析方法来说比较简单，能大大简化设计计算工作，同时它能够清晰地反映出结构在强震作用下各个方面的性能，尤其对于反应以基本振型为主的结构，Pushover分析方法不仅能够很好地反映结构的整体变形，还能够很清晰地反映结构局部的塑性变形机制，相对于传统的线弹性静力法，它能够检测出线弹性静力法所不能检测到的结构缺陷，如局部楼层过大的变形、强度的不均匀分布和潜在易破坏构件的局部过载等问题［9］．一些国家的抗震规范己逐渐接受了这一分析方法并纳入其中，如美国的ATC-40［10］、FEMA-273和FEMA-274［11］，日本、新西兰等国的规范．我国在新的建筑结构抗震设计规范中也引入了Pushover分析方法．

1 Pushover分析方法的基本原理

Pushover方法作为一种结构抗震能力评价的新方法，主要通过对现有结构或设计方案进行抗侧力的计算，从而估计其抗震能力．其主要原理是:根据结构的具体情况，在结构上施加某种分布的侧向力并逐步单调增加，使结构从弹性阶段开始，经历开裂、屈服直至破坏倒塌，从而获得结构能力谱曲线，并将结构能力谱曲线和地震反应谱曲线画在同一坐标系上，通过对比来评估结构在给定地震作用下的反应特性［12］．目标位移的确定和加载模式的选择直接影响Pushover分析方法的抗震评估的准确性．利用静力弹塑性分析进行结构分析的优点在于既能对结构在多遇地震下的弹性设计进行校核，也能够确定结构在罕遇地震下潜在的破坏机制，找到最先破坏的薄弱环节，从而使设计者仅对局部薄弱环节进行修复和加强．不改变整体结构的性能，就能使整体结构达到预定的使用功能．

Pushover分析方法本质上是一种与反应谱相结合的静力弹塑性分析方法，它的基本思路是将地震荷载等效成侧向荷载，采用对结构施加呈一定分布的单调递增的水平力的方式，用二维或三维的力学模型代替原结构，按预先确定的水平荷载加载方式对结构进行推覆分析，逐步将结构推至一个给定的目标位移来研究分析结构的非线性性能，从而判断结构及构件的变形受力是否满足设计要求．

2 基本假定

Pushover方法一般基于以下两个基本假定:

(1)结构(实际工程中一般为多自由度体系，简称MDOF)的响应与该结构的等效单自由度体系(简称SDOF)相关，这表明结构的响应基本上由结构的第一振型控制;

(2)结构沿高度的变形由形状向量{Φ}表示，在整个地震反应过程中，不管结构的变形大小，形状向量{Φ}保持不变．

严格来说，这两个假定是不完全准确的，但是己有的研究表明，对于响应以第一阶振型为主的结构，该方法可以得到较合理的最大地震反应估计(尤其对于基本周期小于ls的结构)［13］．

3 实施步骤

推倒分析法的实施步骤为:

(1)准备结构数据．包括建立结构模型、恢复力模型，估计塑性铰可能出现的部位．

(2)计算结构在竖向荷载作用下的内力，将其与水平力作用下的内力叠加，作为某一级水平力作用下构件的内力，以判断构件是否开裂或屈服．水平加载模式指侧向力沿结构高度的分布方式，用来表示设计地震中的反复力作用．推倒分析的关键之一就是选择适当的侧向推力分布模式，结构在这些侧向力的作用下逐步达到目标位移或倒塌状态．迄今为止，已提出了若干种不同水平加载模式，根据是否考虑地震过程中层惯性力的重分布可分为两类:一类是固定模式，另一类是自适应模式．固定模式是指在整个加载过程中，侧向力分布保持不变，不考虑地震过程中层惯性力的改变．自适应模式是指在整个加载过程中，随结构动力特性改变而不断调整侧向力分布．

(a)均布加载模式．水平侧向力沿桥墩高度分布与节点质量成正比的加载方式称为均布加载模式，属于固定模式．其数学表达式可表示为:

式中:Pi为第i个节点水平荷载;Vb为桥墩底部剪力;n为桥墩总节点数．

(b)倒三角分布水平加载模式．水平侧向力沿桥墩高度分布与节点质量和高度成正比(即底部剪力法模式)的加载方式称为倒三角分布水平加载模式，属固定模式．其数学表达式可表示为:

式中:Wi为桥墩第i个节点重力荷载代表值;hi为桥墩第i个节点距墩底的高度．

(c)随振型而变的水平加载模式．基于结构瞬时振型采用振型分解反应谱法平方和的平方根(SRSS)决定水平侧向力分布的加载方式称为随振型而变的水平加载方式，属自适应模式．其基本作法是利用前一步加载获得的桥墩周期与振型，采用SRSS确定桥墩各节点处基本振型．其数学表达式为:

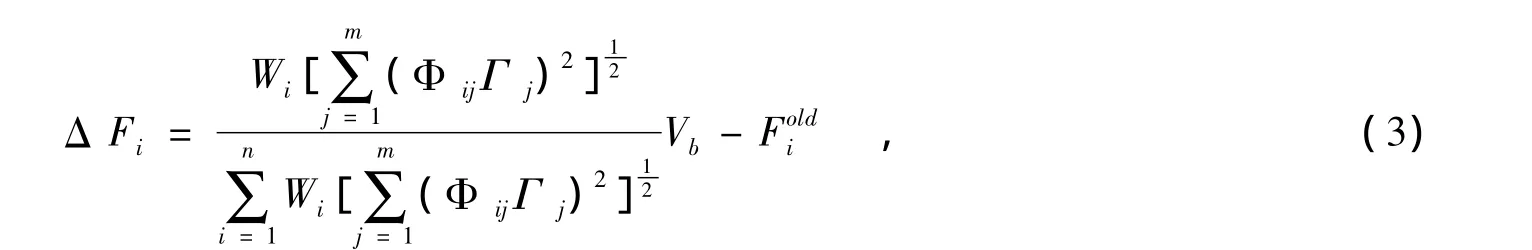
式中:Wi为桥墩第i个节点重力荷载代表值;Φij为前一步第j模态第i个节点处的振型;Γj为前一步加载振型参与系数;m为采用的模态数;n为节点总数;Vb为此步基底剪力;Foldi为前一步节点i处的水平荷载．

(3)在结构质心处，施加某种侧向水平荷载．水平力产生的内力与步骤(2)所计算的内力叠加后，使一个或一排构件开裂或屈服．

(4)对于开裂或屈服的构件，对其刚度进行修改后，再施加一级荷载，使得又一个或一批构件开裂或屈服．

(5)不断重复步骤(3)和(4)，直至结构顶点位移足够大或塑性铰足够多，或达到预定的破坏极限状态．

(6)绘制用Pushover分析方法得到结构的推倒分析曲线，即基底剪力和顶点位移之间的关系．

4 数值算例

某双柱简支梁桥，位于8度Ⅱ类场地，墩底到盖梁中心的高度H=11．2 m，墩底到盖梁底面的高度h=10．0 m，两墩柱中心距离为4 m，墩柱的横截面为2 m×2 m的正方形，墩柱墩帽均采用C30钢筋混凝土．二期恒载及箱梁的总重量W=9 470 kN．结构示意图见图1．

本算例采用美国伯克利分校结构分析有限元软件OpenSees进行分析计算，模型中的墩柱和盖梁均采用非线性梁柱纤维单元来模拟，墩底固结，塑性铰采用分布塑性铰．弯矩-曲率关系是进行桥梁结构弹塑性分析的最基本的一步．使用美国的UCFyber软件计算出塑性铰区的弯矩-曲率关系．其中，混凝土采用Mander应力-应变模型，而钢筋的应力-应变采用理想弹塑性应力-应变关系．

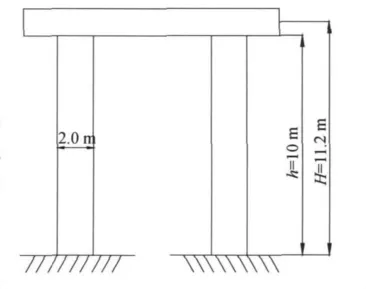
图1 双柱桥墩结构图

5 计算结果分析

5．1 不同侧向力分布模式的影响

计算高度为11．2 m的桥墩，当墩底剪力相同时，采用3种侧向推力模式分别计算列入表1．3种侧向推力模式，从表1的数据可以看到3种模式的结果接近．采用模式(3)得出的屈服位移与屈服剪力最

小，但由于桥墩质量主要集中于墩顶．为简化计算，完全可以采用模式(1)．

表1 不同侧向推力模式下桥墩位移和内力(计算高度11．2 m)

5．2 不同计算高度对桥墩抗震性能的影响

取计算高度分别为8、11．2和15 m双柱墩进行分析，截面尺寸和配筋均不变，它们的位移延性系数分别为10．5、9．7、7．6．因此，在截面和截面材料特性相同的条件下，墩越高，具有的位移延性系数越低(图2～4)．

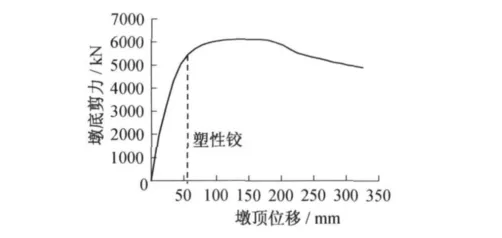
图2 计算高度11．2m的双柱墩的Pushover曲线

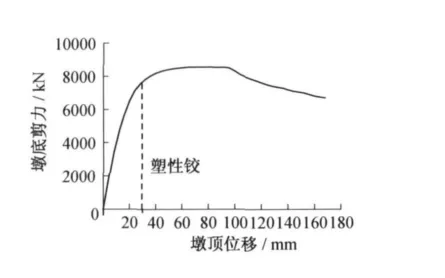
图3 高度8m的双柱桥墩Pushover曲线

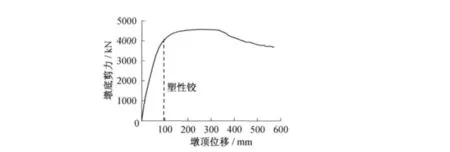
图4 高度15 m的双柱桥墩Pushover曲线

5．3 不同的纵向钢筋配筋率对桥墩抗震性能的影响

桥墩计算高度11．2 m，横截面尺寸2 m×2 m，当纵向钢筋的配筋率分别为2%、2．5%、3%时，桥墩内力和位移计算结果如表2所示，随着墩柱纵向钢筋配筋率的增大，墩底最大剪力增大，抗剪强度增大，但是位移延性系数降低，桥墩延性能力减弱．抗震能力Pushover分析曲线如图5～7所示．

表2 不同纵向钢筋配筋率的桥墩内力和位移(计算高度11．2 m)

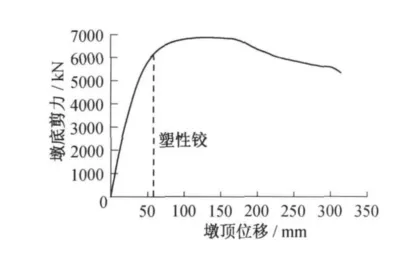
图5 纵筋配筋率2%的Pushover曲线

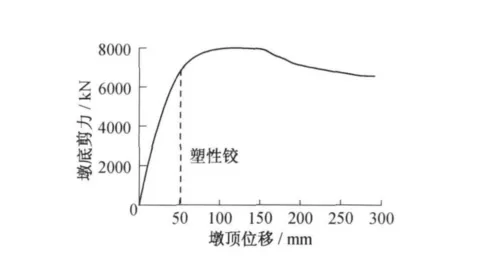
图6 纵筋配筋率2．5%的Pushover曲线

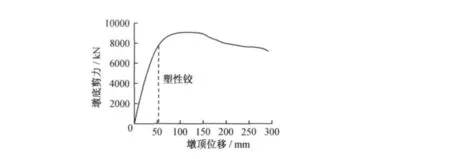
图7 纵筋配筋率3%的Pushover曲线

6 结论

(1)在3种不同的侧向力模式作用下，桥墩的墩底剪力和墩顶位移结果比较接近，同时由于桥梁上部结构质量主要集中于墩顶，因此，为了简化计算，可以采用模式(1)，即在墩顶作用一个集中侧向力．

(2)从桥墩Pushover分析曲线上可以看出，在截面尺寸和材料特性相同的情况下，随着桥墩高度的增加，桥墩的极限位移增大，但位移延性系数降低．

(3)桥墩延性能力随着纵向钢筋配筋率的提高而降低，说明桥墩设计时要配置合适的纵向钢筋．

［1］FREEMAN SA，NICOLETTI J P，TYRELL J V．Evaluations of existing buildings for seismic risk-A case study of Puget Sound Naval Shipyard，Bremerton，Washington［C］．Oakland，California:Proc 1st U SNational Conference on Earthquake Engineering，1975:113 －122．

［2］叶燎原，潘文．结构静力弹塑性分析(PUSHOVER)的原理和计算实例［J］．建筑结构学报，2001(1):37－43．

［3］KRAWINKLER H，SENEVIRATNA G．Pros and cons of a pushover analysis of seismic performance evaluation［J］．Engineering Structures，1998，20(4 －6):452 －464．

［4］CHOPRA A K，GOEL R K．CaPacity demand diagram methods for estimating seismic deformation of inelastic structures SDF system．PEER － 1999/02［R］．Berkeley:Pacific Earthquake Engineering Research Center，University of California，1999．

［5］孙景江，TETSURO O，赵衍刚，等．Lateral load pattern in pushover analysis［J］．地震工程与工程振动:英文版，2003(1):99－108．

［6］魏巍，冯启民．几种Pushover分析方法对比研究［J］．地震工程与工程振动，2002，22(4):66－73．

［7］王理，王亚勇，程绍革．空间结构非线性静力分析的工程应用［J］．建筑结构学报，2000，21(1):57－62．

［8］叶献国，钟迅，李康宁，等．Pushover方法与循环往复加载分析的研究［J］．合肥工业大学学报:自然科学版，2001，24(6):1019－1024．

［9］冯峻辉，闫贵平，钟铁毅．地震工程中的静力弹塑性(pushover)分析法［J］．贵州工业大学学报，2003，23(2):89－102．

［10］Applied Technology Council．Seismic evaluation and retrofit of concrete building ATC －40［R］．Oaklamd:Applied Technology Council，1996．

［11］NEHRP．Commentary on the guidelines for the rehabilitation of building FEMA273，FEMA274［S］．Washington D C:Federal Emergency Management Agency，1996．

［12］PRIESTLEY M J N．桥梁抗震设计与加固［M］．北京:人民交通出版社，1997．

［13］范立础．桥梁抗震［M］．上海:同济大学出版社，1997．