基于抗饱和PI调节器的BUCK变换器的设计与实现

江 澜，蔡 文

(上海师范大学信息与机电工程学院，上海200234)

0 引言

PID控制是发展最早、应用最广的一种控制策略，由于其算法简单、鲁棒性较好、可靠性高，被广泛应用于各类工业控制的算法设计中［1－2］，特别在不完全了解一个系统或被控对象的实际参数，或不能通过有效的测量手段来获得准确的系统参数时，往往采用PID控制［2］．

在电力电子变换器的设计中，由于系统本身是一个非线性、时变系统，因而常常采用PID控制器进行设计．在实际应用中，由于系统对快速性的要求不那么高，因而在系统设计中常常采用PI调节器［1］．在PI调节器的设计中，若PI算式中的积分量积累了过大数值，以至于超出执行元件的极限能力，就会出现积分饱和现象［1－2］，进而影响系统性能．本文作者基于TI公司的DSP2812设计并实现了一种抗饱和的数字PI调节器，将其应用于BUCK变换器的控制中，采用电流、电压双闭环控制［3］，取得了良好的动、静态性能．

1 BUCK电路结构

BUCK变换器的基本电路拓扑结构如图1所示［4－5］，其中DC为输入的直流电压，全控型器件IGBT作为开关管V与反向并联的续流二极管VD一起构成控制模块，以控制从电源端输出到负载端的能量．图1中L和C构成低通滤波电路，Z为负载．设主回路电流为IL，输出直流电压为Uo．

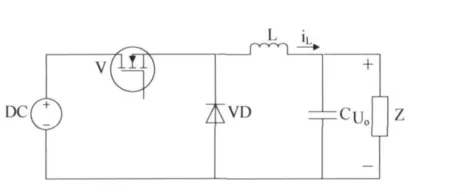
图1 BUCK电路原理图

图2是开关管V导通时的等效电路［4－5］．当V闭合时，直流电源向负载供电，在此阶段，电感L充电储能，主回路电流呈线性增长，续流二极管VD由于两端施加反向电压而截止．

图3是开关管V截止时的等效电路［4－5］．当开关管V截止时，直流电源与负载端开，电感L释放能量，二极管VD续流．在此阶段，电感L通过负载放电，主回路电流线性减小．为了使输出电压满足要求，有必要在负载端并联合适的电容．

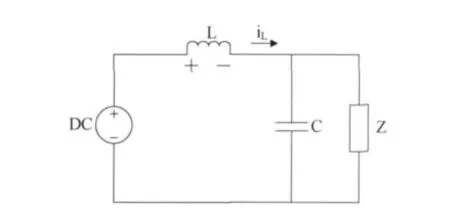
图2 开关V导通时的等效电路

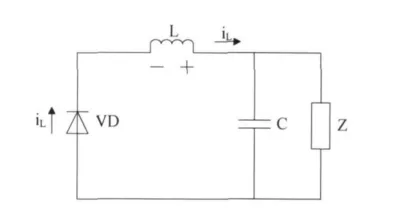
图3 开关V断开时的等效电路

BUCK变换器可以输出两种类型的直流电压［6］:一是输出电压可在一定范围内调节控制;二是输出一个恒定的直流电压．本次设计的是输出恒定电压的BUCK变换器．

2 BUCK变换器闭环控制系统及抗饱和数字PI调节器的设计

2．1 BUCK变换器闭环控制系统

为提高BUCK变换器的静态、动态性能，采用电压外环、电流内环的双闭环控制系统［3］，示意图如图4所示．

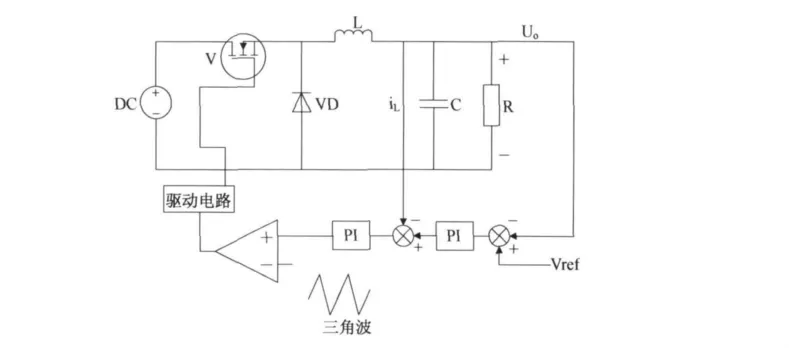
图4 BUCK变换器控制示意图

在图4中，将参考电压Vref与检测到的输出电压Uo相减，结果送入电压环的PI调节器，该PI调节器的输出信号即为电流内环的参考输入信号．同时，将在主回路中检测到的电流IL作为反馈信号与电流参考信号相减，结果送入电流环的PI调节器，并与三角载波做比较，得到开关管V的PWM脉宽调制信号．BUCK变换器控制系统框图如图5所示，其中的电流内环能够限制主回路最大电流，快速抑制电源扰动;电压外环，能够稳定输出电压．

2．2 抗饱和数字PI调节器的设计

PI调节器的控制规律为［2－3］:

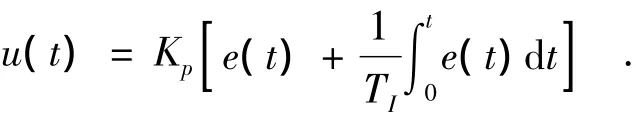
其中，u(t)为PI控制器的输出，e(t)为PI调节器的输入，Kp为比例系数，TI为积分时间常数．对上式进行离散化处理，则PI控制算法表达式为:

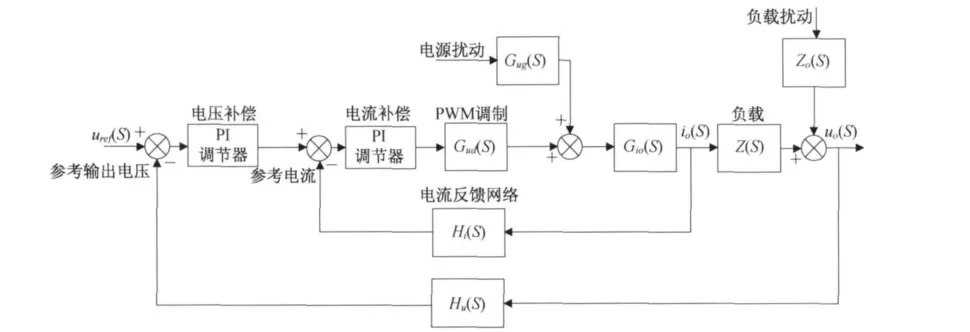
图5 双闭环控制系统框图

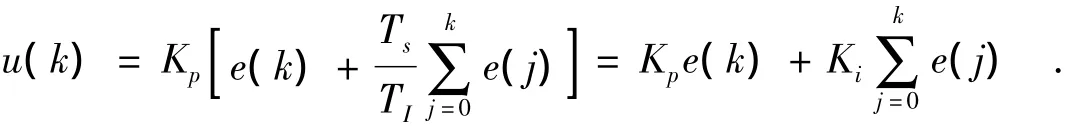
其中k=0，1，…，表示采样序列，u(k)表示第k次采样时刻PI调节器的输出值，e(k)表示第k次采样时刻输入的偏差值，Ts表示采样周期，Kp为比例系数，Kt为积分系数．

常用的数字PI调节器有位置式和增量式控制算法［2］．采用位置式算法:PI调节器的输出可以直接控制执行机构．这种算法的优点是计算精度比较高，缺点是每次都要对e(k)进行累加，容易出现积分饱和现象．一旦出现积分饱和的情况，就会引起执行机构位置的大幅度变化，造成被控对象的不稳定．为抑制这种情况的出现，采用位置式抑制积分饱和的PI算法，其表达式为:

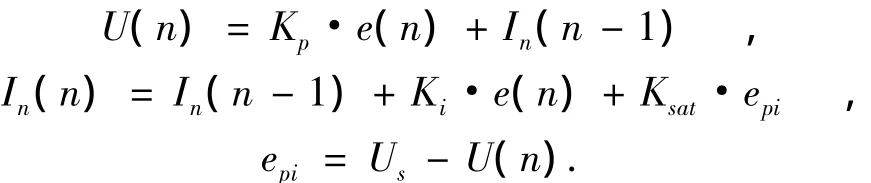
其中:当 U(n)≥Umax时，Us=Umax;当 U(n)≤Umin时，Us=Umin．Us为PI算法的饱和输出;U(n)表示本次的PI调节器的计算结果;Kp为比例调节系数，Kt为积分系数，Ksat为抗饱和系数，In(n)为本次积分累加和，Umax、Umin分别为PI调节器输出的最大值和最小值．抗饱和PI调节器算法的程序框图如图6所示．

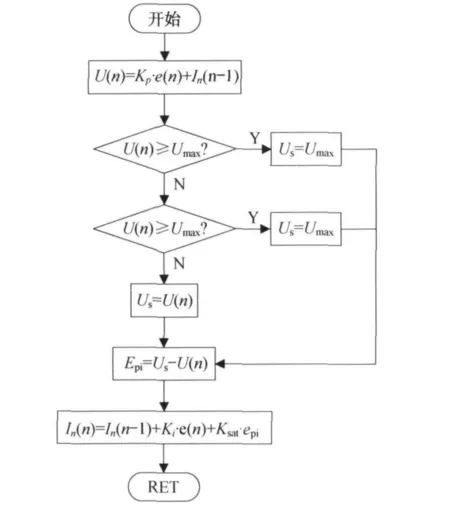
图6 抑制积分饱和的PI算法

3 实验结果及其分析

为验证设计的效果，在一台功率为5．5 KW的BUCK变换器的实验平台上进行了实验．在图1中的输出端并联390μF/500 V电容，在主回路中串联的电感容量为1205μH，开关频率为20 KHz．主电路中的电压、电流检测均由霍尔传感器实现．

经过处理后的模拟量送入DSP内置的A/D口，完成到数字量的转换，各种运算及控制算法均由DSP编程实现．

可变直流输入电压最大为60 V，设输出稳定直流电压为15 V，带电阻性负载，进行了以下实验:

(1)电源电压变化:输入电压从20 V突增到30 V，得到的输出电压、输出电流及PWM控制信号波形如图7所示．

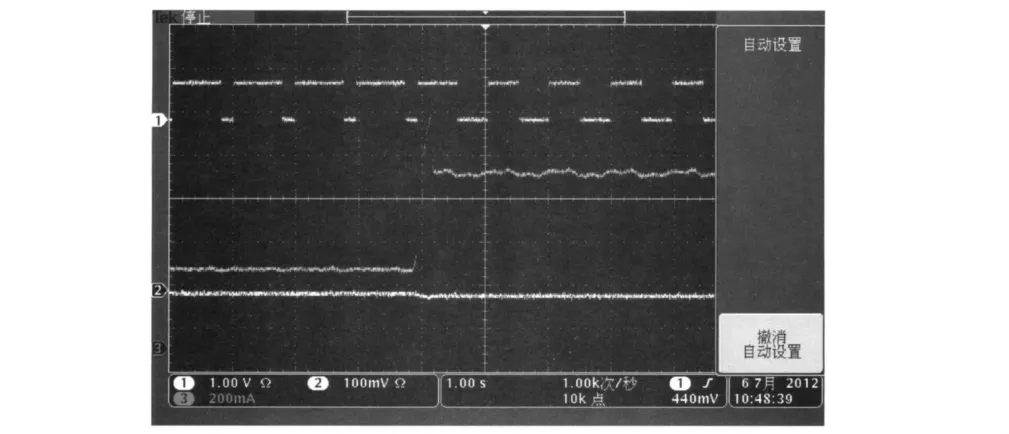
图7 电源扰动时驱动信号、电流、电压波形

(2)改变负载大小:将负载从18．3Ω突加到27．5Ω，得到电压、电流及PWM控制信号波形如图8所示．

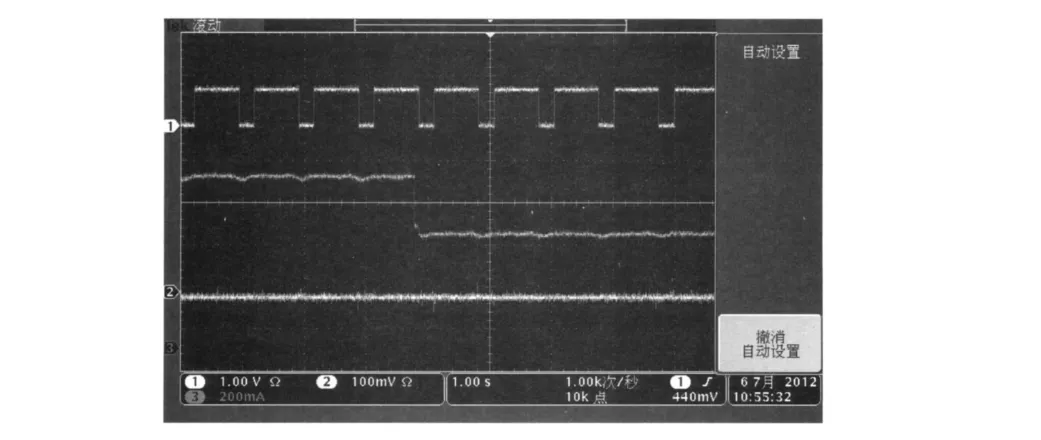
图8 负载扰动时驱动信号、电流、电压波形

图7、8中的波形为数字式多踪示波器的输出结果，其中第1踪为开关管V的驱动信号;第2踪为主回路电流波形，第3踪为输出电压波形．

由图7可见，PWM信号脉宽变窄，电流突增，但经过短暂时间后(小于100 ms)，电流趋于稳定．电压经过微小扰动后同样趋于稳定．

由图8可见，随着负载的改变，主回路中的电流随之改变，但是输出电压稳定．

4 结论

由于PID参数直接影响着控制效果的好坏，本文作者采用工程整定方法，依赖工程经验，直接在控制系统的实验中进行PI参数整定［2］，方法简单、调整方便．将有抑制饱和积分功能的PI调节器运用于BUCK变换器的电压外环、电流内环的设计中，起到了稳压限流的作用，系统取得了良好的动、静态性能［6］．实验结果验证了设计的有效性．

［1］ALI E，ALIREZA K，ZHONG N，et al．连晓峰译．集成电力电子变换器及数字控制 ［M］．北京:机械工业出版社，2011．

［2］白志刚．自动调节系统解析与PID整定［M］．北京:化学工业出版社，2012．

［3］BUTI B，NAGY I．Stability analysis of PWM-controlled dual channel resonant buck converter using PI controller［C］∥IEEE SPEEDAM 2006，Palazzodei Congressi Taormina:IEEE Inc，2006:208 －213．

［4］杜飞，林欣．电力电子技术的MATLAB仿真［M］．北京:中国电力出版社，2009．

［5］曹霞，关振宏，黄栋杰，等．Buck变换器在Matlab/Simulink下的仿真研究［J］．电器开关，2009，47(6):23－25．

［6］BRADLEY M，ALARCON E，FEELY O．Analysis of limit cycles in a PI digitally controlled buck converter［C］∥IEEE ISCAS 2012，Seoul:IEEE Inc，2012:628 －631．