我国黄金价格收益率及其波动性研究——基于ARMA与GARCH族模型

西南财经大学经济信息工程学院 黄宇梦

我国黄金价格收益率及其波动性研究
——基于ARMA与GARCH族模型

西南财经大学经济信息工程学院 黄宇梦

本文使用2002年10月31日到2013年5月23日共2578个交易日的Au99.95的黄金现货价格，对其建立ARMA、GARCH模型，发现其日收益率存在波动聚类的现象，而TARCH模型则揭示其收益是非对称的，在黄金市场，价格波动受利好消息影响更大。

黄金价格 收益率 波动性 GARCH族模型

黄金一直是投资者较为喜爱的一种投资选择。最近几年，特别是在后金融危机阶段的美元危机，刺激了对黄金投资和投机需求的增加，在黄金市场上的反映是黄金价格的波动性加剧和风险的聚集。但最近，黄金价格却呈现出震荡下跌的趋势，许多疯抢黄金的“中国大妈”们被套，黄金前景雾气蒙蒙。因此，有必要对黄金收益的波动性有一定的分析和认识，从而更理性地对黄金进行投资。

GARCH模型能够较好地捕捉金融市场的真实波动性特征如前所述的波动的聚集性，所以本文将在接下来的分析中，首先对黄金价格的对数收益率进行GARCH模型的拟合；又由于现实中市场对利好和利空消息的反应往往显示出非对称性(即杠杆效应)，所以将用TGARCH模型对黄金的对数收益率进一步进行建模以与GARCH模型进行比较。

1 数据描述性统计

本文选用的数据是从2002年10月31日到2013年5月23日共2578个交易日的Au99.95的黄金现货价格。

1.1 数据走势

对黄金价格进行对数处理，Is=100*log(x(t)/x(t-1))，做出对数收益率的时间序列走势图，如图1所示。

图1 黄金价格对数收益率走势

从上图可以看出，黄金现货收益率的波动基本围绕均值0上下波动，但是有一定的波动率聚类现象，即波动率较大的时刻基本处于某一时点左右，且每一次大的波动之后都紧跟着另外一个大的波动，可能存在一定的条件异方差现象。

1.2 描述性统计

其数理统计特征如表1所示。

表1 黄金收益率描述统计

观察其数理统计特征，黄金现货日收益率的平均值为0.046748，中位数为0.088067，都大于0，且其偏度为-0.550491<0，也即在对数收益率在均值左边的频数比右边的频数小，故其为一左偏分布。且其统计特征中峰度为10.44856>3，故其为比正态分布更尖峰的分布。

再看其Jarque—Bera检验结果为6087.433，P值为0，故可拒绝原假设，时间序列数据服从正态分布，即黄金现货收益率的波动不服从正态分布。

2 现货黄金收益率的波动性研究

2.1 平稳性检验

传统的时间序列模型要求数据必须是平稳的，所以首先要检验数据的平稳性。本文采用单位根方法检验日对数收益率的平稳性，对黄金现货价格收益率序列进行ADF检验。检验结果显示，该序列的ADF检验统计量为-53.17573，明显小于显著水平为1%时的-3.432695，因此拒绝存在单位根的原假设，即该自然对数收益率在1%标准下是显著平稳的。因此可以直接利用其收益率进行进一步的建模。

2.2 相关性的考察及AR模型的建立

接着考察其滞后20期的自相关和偏向关系数，以便用ACF和PACF定阶的方法对其建立初步的模型。

通过对自相关和偏向关系数的观察，可以发现日收益序列的第二阶相关性较为显著。初步确定可以对其建立AR(2)、MA(2)或ARMA(2，2)模型。经过对这些模型的逐步回归，可以看出AR(2)模型的拟合效果最好，因此选择采用AR(2)模型进行拟合。利用最小二乘法得到该模型的回归结果为：

AR(2)的系数在1%的显著水平下是统计显著的。AIC准则为3.126239，BIC准则为3.1301785，回归标准误差为1.154645，残差平方和为3430.335。

2.3 AR模型残差序列自相关检验

再对回归之后的残差序列进行检验。

回归方程的残差序列图表明其存在丛集性效应，即一次大波动后伴随着较大幅度的波动，一次小波动后伴随着较小幅度的波动。说明该模型存在着自回归条件异方差现象的可能性很大，因此有必要对模型的残差序列进行 ARCH-LM 检验。

结果表明，在滞后3期(由BIC准则确定)的时候ARCH-LM检验的F统计量为42.08234，R2的值为120.5188，P值均为0。所以拒绝原假设，说明黄金现货价格日收益率序列的自回归方程残差存在ARCH效应，回归方程残差平方序列存在自相关。

图2 AR(2)模型残差图

2.4 建立GARCH(1,1)模型

因为GARCH模型可以很好地替代ARCH模型，且不会出现当ARCH模型阶数较高时产生的参数估计不准确的现象，因此可以采用GARCH模型来表示日收益率及波动性。对于其阶数选择，由AIC和BIC准则最终确定为GARCH(1,1)。

表2 GARCH(1,1)模型

由GARCH(1,1)模型可知，均值方程：

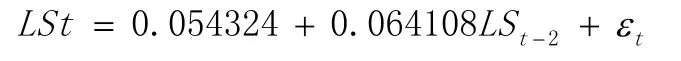
条件方差方程：

从而得到了关于现货黄金收益率的均值方程和方差方程，再次利用ARCH-LM检验。

2.5 GARCH模型残差序列自相关检验

滞后阶数为3阶时，F统计量为0.161423，R2的值为0.484932，P值均大于0.05，表明模型的误差序列已不存在自回归条件异方差。ARCH项系数与GARCH项系数之和为0.976712，符合平稳约束条件，过去的波动对未来的影响呈逐渐递减趋势；另一方面，二者之和非常接近于1，说明过去波动的冲击较为持久，对未来的预测有着重要的作用。

3 现货黄金收益波动非对称性研究

尽管GARCH(1,1)具有描绘金融数据方差自相关性等诸多优点，但是它不能够体现对金融市场波动的非对称效应。金融市场波动具有杠杆效应，即负面冲击和正面冲击引起的市场波动可能不同。

在分析非对称波动效应的各种ARCH模型中，TARCH模型是结构简洁并能直接反映价格受正负冲击影响差异程度的一类模型。因此，可以利用TARCH模型考察新息冲击曲线的对称性。

TARCH模型回归结果显示，非对称系数显著异于0(P=0.00 10)，表明TARCH模型较好地体现了现货黄金价格波动非对称性的特点。这里应注意到，非对称系数λ=-0.026515意味着在黄金市场中，对波动率的影响方面，利好消息比利空消息更明显，这也有异于股票等金融资产波动规律的现象。

4 结语

(1)现货黄金日收益率是不服从正态分布的，这是因为它具有很明显的尖峰厚尾的特征，并且有明显的ARCH效应，即存在波动的聚类性。大波动后跟大波动，小波动后跟小波动。

表3 TARCH(1,1)模型

(2)GARCH模型相对于AR、ARCH模型能更好地反映收益的动态变化、丛集效应和非对称特征；能够更好地处理收益率序列的异方差性；在较少的参数下，能更好地刻画收益率序列的波动性。

(3)文中garch模型中的ARCH项系数和GARCH项系数之和为0.976712，接近于1。说明过去的冲击对价格的影响会持续很久，即影响是长期的。从AR(2)回归模型也可以看出，滞后两期的收益率与当日收益率仍有正的相关关系，影响较长久。

(4)TARCH(1,1)模型中，非对称系数结果表明在黄金市场上，利好消息对黄金价格的波动的影响要大于利空消息对黄金价格的波动影响，即黄金价格在上涨过程中的波动更大。这跟黄金是一种特殊的投资产品有关。黄金价格大幅上涨往往出现在经济低迷、复苏前景不明朗或是通胀压力较大的情况下，投资者基于规避风险和保值的目的会大量增加黄金购买，从而推动黄金价格的上涨并造成较大的波动。联想到最近市场上黄金价格下跌的情况，因为全球通胀压力的减小，减轻了黄金规避通货膨胀功能的吸引力，利空消息导致金价的下跌。但即使大幅下跌，造成包括“中国大妈”在内的各路人士疯抢黄金，也没能力挽狂澜对黄金价格造成较大的冲击，黄金价格依旧在下跌。由此也可以证明，利好消息影响更大，与TARCH模型的分析是非常吻合的。

[1]曹野.基于GARCH族模型的黄金价格收益率及波动性研究[J].价值工程,2012,31(2).

[2]钟!,周汉臣,孙清芬.黄金价格波动效应研究[J].今日南国(理论创新版),2009(4).

[3]孙喻哲.国内黄金价格收益率波动性研究——基于ARMA与GARCH模型的分析与预测[J].时代金融,2012(29).

[4]梁维全.黄金价格波动的影响因素的实证研究[J].中国证券期货,2009(5).

[5]郑秀田.基于GARCH类模型的我国黄金市场波动特征研究[J].中国物价,2009(10).

[6]史代敏,谢小燕.应用时间序列[M].高等教育出版社,2011.

[7]郑秀田.基于GARCH-M模型的黄金市场风险与收益关系研究[J].黄金,2008(5).

[8]温博慧.国内外黄金价格波动性及其演化的实证研究——以中国上海和英国伦敦黄金市场为例[J].世界经济情况,2008(10).

F224

A

1005-5800(2013)08(a)-134-02