基于输入整形的起重机消摆控制研究进展

任会礼，付玲，梅志千，高常春，李向国，孙雷

(1.中联重科股份有限公司建设机械关键技术国家重点实验室，湖南长沙410013;2.河海大学机电工程学院，江苏 常州213022)

0 引言

随着生产规模的扩大，自动化程度的提高，作为物料搬运重要设备的起重机在现代化生产过程中应用越来越广，作用越来越大，它的运行性能将直接影响到整个生产过程的效率与安全性。

起重机由于吊重惯性与悬索构成的摆系统，在其运行过程中，尤其是在启动和制动阶段，吊重会产生摆动，其摆动幅度与加减速度成一定的比例关系。因此效率要求越高的应用场合，吊重的摆动幅度也越大。目前起重机械自动化程度普遍不高，虽然国内外也有一些具有一定自动化程度的起重机械，但是由于起重机往往作业在诸如船厂、机械加工车间和建筑工地等非结构化的环境，这就对现有的大多数吊重消摆技术实际应用带来困难，起重机作业更多的还需要依靠司机经验，误差难于控制。在起重机械进行装卸作业时，平均有超过30%的时间浪费在起重机械的对位上。此外，对海上作业的大型起重机械来说，由于起重量大，运行速度快以及受风浪的作用，吊重摆动问题更加突出，一旦发生与结构物的碰撞，将引发灾难性的后果，这就对装卸作业平稳性及安全性提出了更高的要求。一般来说海况等级达到3级时，由于吊重摆动幅度所引起的危险性将导致海上作业的大型起重机械不得不停止作业。据统计，我国东海适合起重机械安全作业的时间仅占总数的34%，而在国外，北海适合起重机械安全作业的时间也不到总时间的一半。

综上所述，在起重机的启动和制动过程中如何减小甚至消除吊重的摆动就成为该领域关注的重点问题。近些年来发展出来的起重机消摆实用开环控制技术主要有：输入指令滤波、输入指令整形控制等。

1 输入指令滤波控制

众所周知，在吊重摆角较小的情况下，龙门吊、行车和桥吊等起重机吊重惯性与悬索可以简化为式(1)所示的单摆动力学数学模型，

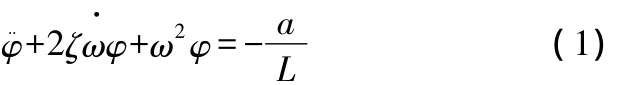
在实际应用中，一般多采用梯形作为吊点或小车速度曲线，即吊点或小车的加速度a是如图1所示的方波单脉冲信号，由于加速度信号a中具有与式(1)所示系统的固有频率相同的谐波成分，因此在起重机吊点加速、减速过程结束后，吊重的摆角φ响应将是如图1所示的等幅震荡，显然会对起重机的高效与安全作业带来不利影响。

图1 常规单次加、减速时吊点速度、加速度和吊重摆角曲线

对起重机吊点或小车加速度信号作滤波处理，消除其中与式(1)所示系统的固有频率相同的谐波成分，以避免产生图1所示的吊重在加、减速结束后的残余等幅振荡就成为抑制起重机吊重摆角波动的自然选择方法［1］。Parker设计中心频率为式(1)所示系统固有频率的输入整形3阶带阻滤波器，对船用吊杆起重机的回转、降幅和起升运动的输入信号中的与吊重摆动的固有频率相同的谐波成分进行陷波处理，在1/16吊杆起重机物理模型中的应用表明：吊重摆动降幅达18dB，另一方面，由于带阻滤波器的引入而导致回转、降幅和起升运动的响应延迟［2］。M.A.Ahmad等采用 Butterworth 3、6、9 阶低通滤波器方法，低通滤波器和带阻滤波器结合LQR最优控制方法分别实现起重机的输入跟踪和吊重摆角的波动抑制。分析表明：带阻滤波器对吊重摆角波动的抑制能力要优于同阶的低通滤波器，而且其抑制能力随着滤波器阶次的增加而增强［3，4］。对起重机的输入加速度信号进行滤波处理，其代价是跟踪响应速度的降低，即滤波作用普遍存在输入指令的迟后影响［3-5］。

2 输入指令整形控制

针对输入指令滤波控制方法所存在的不足，Smith提出了一种在结构与实现方式上与滤波控制方法不同的控制方法。该方法能够使轻阻尼或零阻尼系统对起重机吊点或小车的加速度阶跃输入产生无振荡响应，这种方法最简单与常见的是把图1中加速度分两次完成，在零阻尼的情况下，每次幅值是总加速度幅值的一半，如果第二次加速度脉冲的施加时间为式(1)所示系统的半周期，那么由第一次激励的等幅振荡将在式(1)所示系统的半周期时由第二次激励的等幅振荡完全抵消，如图2所示［6，7］。这种对式(1)所示系统中的加速度按照一定序列分多次输入的方法称为加速度输入整形控制，对于一般的输入称为输入指令整形控制器(inputting shaper，简称 IS)。

图2 两脉冲加速度整形控制消除吊重残余振荡

理论上来说，上述方法中加速度整形是通过一称作整形控制器的脉冲序列与系统加速度参考信号作卷积而实现的。式(2)是以式(1)所示系统在整形控制作用下的响应与单次加速脉冲作用下的响应的百分比值，即采用IS方法所引起的吊重摆角波动相对于式(1)所示系统中实际固有频率ω的敏感值，该百分比值可以作为IS设计的吊重波动性能指标。

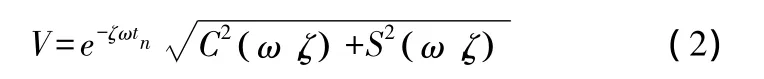
其中：

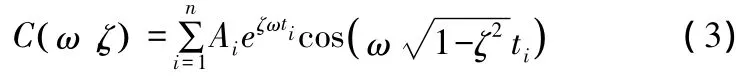
Ai和ti分别是每次加速度脉冲的幅值大小和作用时间。

上述两次加速脉冲序列是最简单的一种输入整形控制方法。两次脉冲的幅值与时间使ω与IS中的系统模型频率ωm相等处的性能指标V=0，也就是式(3)和式(4)要同时为0，即加速或减速结束后吊重摆角的波动为0，因此该方法也称为ZV法(zero－vibration，ZV)。第一个脉冲发生的时间t1=0，为了与单次加速时的摆角幅值保持一致，必须增加一个约束条件：

约束条件式(3)、式(4)和式(5)可以确定ZV法的三个参数：

理论上，如果起重机在作业过程中悬索长度、线性阻尼不变，即式(1)所示系统的模型参数ω， ζ保持为恒定值，ZV法可以在0.5个理论振荡周期内，即0.5Td内完全消除由于起重机小车加速所引起的吊重摆角的波动［8］。而在实际起重机作业过程中，系统模型参数尤其是与悬索长度相关的ω的变化不可避免，这就对ZV法在实际的起重机摆角波动抑制控制中的应用带来了局限性。为了减少ZV法对模型参数的敏感性，学术界提出了ZVD法(zero－vibration and derivative shaper， ZVD)。ZVD 法在ZV法的基础上，增加了V对ω的变化率在ω与IS中的系统模型频率ωm相等处为0的约束条件：

与约束条件(2)为0类似，式(7)同样包含着两个同时为0的约束条件，这两个条件与约束条件式(5)与约束条件式(3)、式(4)同时为0一起可以确定三脉冲ZVD法的五个参数：

ZVD法加速脉冲的时间，或消除吊重摆角的波动的时间为一个振荡周期，即相对ZV延长了0.5Td，这是其不足。ZVD法与ZV法相比其优点是降低了对模型参数的敏感性，提高系统控制的鲁棒性。

为了进一步降低输入整形法对模型参数的敏感性，提高鲁棒性，可以再增加式(2)相对ω的二阶导数为0的约束条件，成为具有四脉冲的ZVDD法。ZVDD法的四个脉冲的对应参数为：

根据对鲁棒性的要求，也可以再进一步增加式(2)相对ω的三阶导数为0的约束条件，使之成为五脉冲的ZVDDD法。ZVDDD法的五脉冲的对应九个参数分别为：

当然每增加一个关于导数的约束条件，其加速脉冲时间就增加0.5Td，即摆角波动抑制时间就延长0.5Td，消摆的响应速度就要降低。

上述分析表明：消摆控制的鲁棒性与消摆速度是一对矛盾，为了增加鲁棒性，同时又不增加加速脉冲数，把式(2)在系统实际的固有频率ω处的V=0的约束条件降低为式(2)具有一定的容许百分比误差Vtol，该输入整形法就是 EI法(extra－insensitive shaper，EI)［9］：

3 输入指令整形控制的鲁棒性分析

在起重机作业过程中，由于悬索长度的变化，吊重摆角的动力学模型参数ζ和ω，尤其ω的变化不可避免，也是必不可少的。因此，各种IS方法对模型参数的不敏感性，即鲁棒性对于IS方法在起重机吊重消摆的实际应用至关重要。

图 3 ζ=0 和 Vtol≤0.05(5%)时 ZV，ZVD，ZVDD和ZVDDD的敏感曲线与不敏感度

为了比较各种IS方法的鲁棒性，定义采用IS方法所引起的吊重摆角波动相对于式(1)所示系统中实际固有频率ω的敏感值，即百分比V≤Vtol时的系统固有频率ω的变化范围，或不敏感度作为鲁棒性评价指标，即频率范围越宽鲁棒性越强。图3是ζ=0，Vtol=0.05 5%( )时，ZV，ZVD，ZVDD和ZVDDD四种输入整形控制方法的鲁棒性比较，图3表明ZV，ZVD，ZVDD和ZVDDD四种输入整形控制方法的实际频率ω与模型频率ωm之比变化范围分别为 0.06，0.29，0.48 和0.63，即实际频率 ω 容许变化范围 是 [0.97ωm，1.03ωm] ， [0.85ωm，1.15ωm]，[0.76ωm，1.24ωm] 和 [ 0.685ωm，1.315ωm]。该变化范围越大表示输入整形控制方法的鲁棒性越强。上述变化范围对应的吊重悬索容许变化范围分别为分别在[0.94lm，1.06lm] ， [0.756lm，1.38lm]，[0.65lm，1.73lm] 和 [0.58lm，2.13lm]变化，lm是相对于消摆控制方法中模型频率ωm的模型悬索长度，摆角波动的百分比仍然V≤Vtol5%( )，明显地随着脉冲数量的增加，鲁棒性增强。但是从式(6)、式(8)、式(9)和式(10)鲁棒性的增强是以对应IS法摆角波动抑制的响应速度的降低作为代价的［9］。

图4 和图5 分别是 ζ=0.05、0.2，Vtol=0.05 5%( )时，ZV，ZVD，ZVDD和ZVDDD四种输入整形控制方法的鲁棒性比较，表明阻尼的增加四种整形方法的鲁棒性得到了增强。

图4 ζ=0.05、Vtol=0.05(5%)时，ZV，ZVD，ZVDD和ZVDDD四种输入整形控制方法的鲁棒性比较

图5 ζ=0.2、Vtol=0.05(5%)时，ZV，ZVD，ZVDD和ZVDDD四种输入整形控制方法的鲁棒性比较

图6是ZVD法与三种EI法的鲁棒性比较，由式(8)、式(11)，ZVD法与EI法的加速脉冲时间，即消摆速度是相同的，在ζ=0的情况下，ZVD法系统实际频率ω与模型频率ωm之比变化范围分别为0.29，而即使变化范围最小的单峰EI法，其系统实际频率ω与模型频率ωm之比变化范围也达到0.4。因此EI法不降低消摆速度，可改善输入整形控制法的鲁棒性。

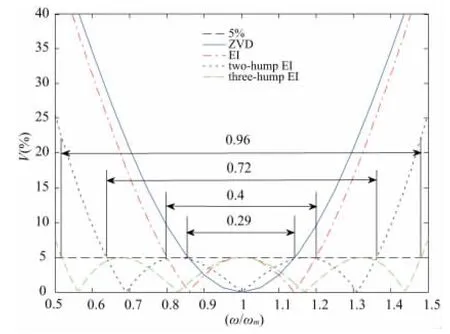
图6 EI法与ZVD法的鲁棒性比较

图7、图8 和图9 分别是 ζ=0、0.05 和0.2 时，单峰、双峰和三峰三种输入整形控制方法的鲁棒性比较，三图表明随在系统阻尼的增加上述EI法的鲁棒性也相应得到了增强。

图7 ζ=0时，各种EI法的鲁棒性比较

图8 ζ=0.05时，各种EI法的鲁棒性比较

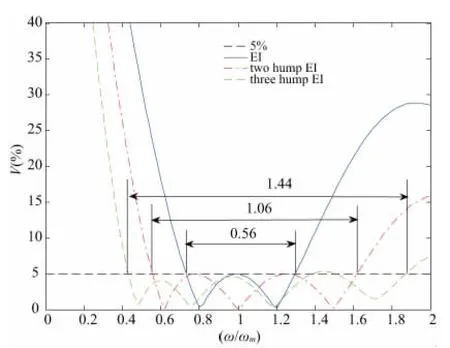
图9 ζ=0.2时，各种EI法的鲁棒性比较

4 输入指令整形控制在起重机消摆控制中的应用

正是由于具有鲁棒性强，只需要对输入信号与脉冲序列进行卷积运算，而不需要反馈控制，从而控制系统结构、算法简单的优点，因此IS方法在起重机吊重消摆控制中得到了广泛的应用。

在起重机的实际应用中，死区、摩擦、传动部件的间隙、饱和和加速度限制等是无法回避的非线性因素。在输入整形控制中考虑逆死区、逆间隙方法可以降低由于死区引起的吊重摆角额外波动，在10t桥吊上的实验表明：即使在死区范围不确定的情况，上述方法仍然可以有效地抑制吊重摆角额外波动［10］。摩擦采用库伦+粘性阻尼进行建模，通过适当的持续激励信号对摩擦模型参数进行离线辨识，以辨识的摩擦模型作为补偿依据和输入整形控制技术共同作用解决摩擦影响，并在塔吊的实验平台上进行了有效性验证［11］。一般的输入指令整形控制作用在起重机小车位置控制环的外部，即开环整形控制方式(outsidethe－loop input shaping，OLIS)，但是在起重机驱动源的饱和和加速度限制因素不可忽略的的情况下，把整形控制器加在起重机小车位置控制环控制器的输出端，即采用闭环整形控制方式(closed－loop signal shaping，CLSS)，在10t桥吊、便携式实验桥吊和塔吊上的实验表明：对由于饱和、加速度限制等非线性对起重机吊重摆角波动抑制，CLSS比采用 OLIS 要优越［12］。

输入指令整形控制技术不仅对如式(1)所示的线性系统的吊重摆角波动抑制有效，而且对如塔吊等回转式起重机的非线性系统的吊重摆角波动抑制也有效。采用传统的整形控制技术时，由于塔吊的回转运动使第二次的加速度脉冲在方向上与第一次的加速度脉冲间存在角度差，从而影响整形控制技术对回转式起重机其吊重摆角波动的抑制效果。解决方法是在两次加速度脉冲中各增加一个径向分量，使两次脉冲前后保持相同方向，以达到与整形控制技术在行车、龙门吊和桥吊等线性动力学系统中类似的吊重摆角波动的抑制效果［13］。

如果在起重作业中悬索长度变化较大，即在吊重动力学系统的固有频率在作业过程变化较大的工况下，整形控制的脉冲频率采用吊重动力学系统在作业过程中的平均固有频率，数值仿真表明吊重摆角的波动的抑制效果比采用吊重动力学系统的初始固有频率值的传统整形控制要好，在15t龙门吊上的实验也验证了上述结论［14］。集装箱起重机的吊重惯性与悬索是一简化的二级摆动力学系统，因此用传统的多脉冲加速度整形控制方法不能够带来理想的集装箱摆角波动的抑制效果;另一方面这种起重机驾驶室往往是与小车一起运动的，因此利用传统的多脉冲整形控制方法的多次加、减速会使司机的操作环境变差，不符合人机工程的设计原则。采用平面四连杆机构对集装箱起重机的悬索建模，结合悬索摆角的相平面轨迹对ZV整形控制进行设计，仿真结果表明比传统的基于单摆动力学数学模型设计的ZV整形控制具有更好的效果［15］。

5 结论

本文分析了两大类输入整形控制法的鲁棒性与消摆速度问题。对于每一类输入整形控制方法，鲁棒性的增强往往导致消摆速度的降低，即消摆控制的鲁棒性与速度存在矛盾。同时从消摆鲁棒性兼具速度的角度，EI输入整形控制方法具有更好的综合性能，而在起重机吊重摆动动力学模型参数，尤其是固有频率变化不大的前提下，ZV类方法的鲁棒性比EI法的鲁棒性要强，在实际应用中应该根据起重机的作业的实际情况，综合两者优点来采用。

［1］Rush D.Robinett，Gordon G.Parker，John T.Feddema，Clark R.Dohrmann，Ben J.Petterson.Sway control method and system for rotary crane.USA Patent，No.5908122，June.

［2］Gordon G.Parker.Experimental Verification of a Command Shaping Boom Crane Control System［C］.Proceedings of the American Control Conference，San Diego，California，June 1999.

［3］M.A.Ahmad，M.S.Ramli，R.M.T.Raja Ismail.Infinite Impulse Response Filter Techniques for Sway Control of a Labscaled Rotary Crane System［C］.2010 Second International Conference on Computer Modeling and Simulation，192-196.

［4］M.A.Ahmad，F.R.Misran，M.S.Ramli，R.M.T.Raja Ismail.Experimental Investigations of Low pass Filter Techniques for Sway Control of a Gantry Crane System［C］.

［5］Hanafy M.Omar.Control of Gantry and Tower［D］.Blacksburg，Virginia：Virginia Polytechnic Institute and State University，2003.

［6］Smith，O.J.M.Posicast Control of Damped Oscillatory Systems［J］.Proceedings of the IRE，vol.45，no.September，pp.1249-1255，1957.

［7］Smith，O.J.M.Feedback Control Systems，pp.331– 345，New York：McGraw－Hill Book Company，Inc.，1958.

［8］singer，N.C.and Seering，W.P.Preshaping command inputs to reduce system vibration［J］.ASME Journal of Dynamic Systems，Measurement，and Control，vol.112，pp.76-82，1990.

［9］ Joshua Vaughan，Aika Yano，William singhose.Comparison of robust input shapers［J］.Journal of Sound and Vibration 315(2008)797-815.

［10］ Khalid L.Sorensen，Patrick W.Cross，William E.singhose，Shashvat Prakash.Analysis and Mitigation of Dead－Zone Effects on System Using Two－Impulse ZV Input Shaping［C］.2007 Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference，DETC2007，v 5 PART B，p 991-1000，2008.

［11］Hanafy M.Omar.Control of Gantry and Tower［D］.Blacksburg，Virginia：Virginia Polytechnic Institute and State University，2003.

［12］John R.Huey，Khalid L.Sorensen，William E.singhose.Useful applications of closed － loop signal shaping controllers.Control Engineering Practice 16(2008)836-846.

［13］D.Blackburn，W.singhose，J.Kitchen，V.Patrangenaru，J.Lawrence.Advanced Command Shaping Algorithm for Nonlinear Tower Crane Dynamics［C］.The 8th International Conference on Motion and Vibration Control(MOVIC 2006).

［14］William singhose，Lisa Porter，Michael Kenison，Eric Kriikku.Effects of hoisting on the input shaping control of gantry cranes［J］.Control Engineering Practice，8(2000)1159-1165.

［15］ Ziyad N.Masoud， Mohammed F. Daqaq. A Graphical Approach to Input－Shaping Control Design for Container Cranes with Hoist.IEEE Transactions on Control Systems Technology，Vol.14，No.6，November 2006：1070-1077.