吊重摆长对起重机PID防摇控制的影响

庞振华，刘 放，吴 涛 ，唐 语

(西南交通大学机械工程学院，成都 610031)

当前，随着自动化的快速发展，起重机的防摇技术成为科学研究的发展方向。目前防摇领域主要分为两部分，包括机械防摇和电子防摇。

机械防摇主要通过设计起重机的机械结构达到防摇的目的。目前，在机械防摇领域，任昭鹏[1]采用一种基于三索限位的机械式防摇摆装置；吴俊杰等[2]提出一种吊盘式机械防摇方案；在电子防摇领域，Lee[3]提出高速负载提升的架空行车防摇摆控制新方法，研究结果表明，上述防摇方式能有效地抑制吊重的摆动。吕锦超等[4]提出了分别控制小车位置、重物摆角的小车-集装箱系统防摇控制方案；李松等[5]提出利用模糊算法与PID控制相结合构成起重机防摆系统；付子义等[6]提出应用最优迭代学习控制的方法,实现对系统的定位以及防摇精确控制；Kawai等[7]提出了一种用于集装箱起重机的带有图像传感器的防摆系统;Yamamot等[8]提出了一种用于定速起重机的简单防摆控制算法；Caporali等[9]提出使用计算机视觉跟踪和自适应粒子滤波来控制闭环中的防晃动，梁利华等[10]研究了电液负载仿真台。

为了提高起重机的工作效率，本文研究了在PID控制器的作用下，影响吊重摆角的因素。采用拉格朗日方程推导动力学模型并对其进行一定简化，最后得出系统的状态方程。通过仿真和试验得出不同摆长的情况下，吊重在控制器下的摆角变化。

1 起重机动力学简化模型

1.1 建立抽象模型

起重机运动模型如图1所示，主要由小车、吊重、摆杆及横梁组成。小车在横梁上通过驱动力F可以来回运动，小车与横梁之间存在阻尼。吊重在小车运动期间可以自由摆动，此处忽略摆动时产生的阻尼。将水平向右设置为小车的正方向，中心线右侧设置为摆角的正方向。

m1为小车质量；m2为重物质量；c为小车与横梁之间的阻尼系数，x为小车的位移，F为小车所受的驱动力；l为吊重长度；θ为重物的角位移图1 起重机抽象模型Fig.1 Crane abstract model

1.2 起重机动力学数学模型

起重机运动模型为欠驱动机构，上述抽象模型包含两个自由度：摆动自由度和水平自由度；小车为驱动机构。定义小车的水平位移x，和吊重摆动角度θ作为该系统的两个广义坐标变量。

系统所受的外力有两种：小车自身的驱动力F和在运动过程中产生的阻尼力cv。由广义坐标变量可建立拉格朗日方程：

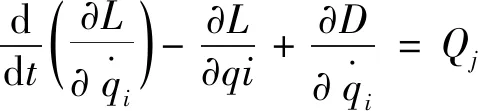
(1)

式(1)中：由于起重机系统为2自由度模型，故qi(i=1,2)为两个广义坐标变量；q1为是小车的位移x，q2为重物摆动角度θ；Qi为系统广义力，由小车位移x建立拉格朗日方程时Qi=F;L为Lagrange函数，它是系统动能V和势能U之差，L=V-U；D为耗散函数：

(2)

由运动合成定理求出重物运动速度：

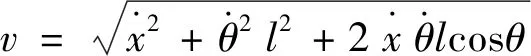
(3)

则系统动能V为

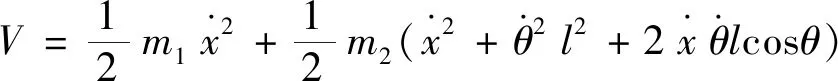
(4)

选取重物最低点作为势能零点，系统势能U为

U=m2g(l-lcosθ)

(5)

将结果代入拉格朗日方程[式(1)]得

(6)

将式(6)写为矩阵形式：

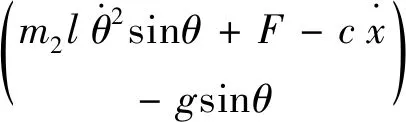
(7)

由于在运动过程中摆角比较小，因此可将式(7)方程进行一定简化：

sinθ≈θ;cosθ=1;sin2θ=0。

化简后的矩阵为

(8)

通过化简后的矩阵可得出系统的状态方程和输出方程：

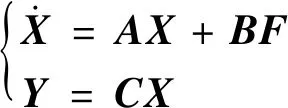
(9)

式(8)中：

矩阵C通过所需的输出量决定。

2 控制算法及原理

PID控制器是一种闭环控制器，它根据给定值ri与实际值输出值yo构成控制偏差：

er=ri-yo

(10)

PID控制规律为

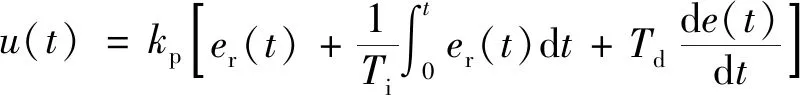
(11)

式(11)可以写为

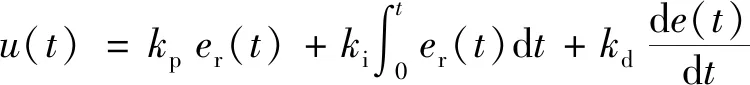
(12)

式(12)中：kp为比例增益；ki为积分增益；kd为微分增益。

PID控制算法通过系统的反馈信号对系统的稳定性进行调节。在起重机运动模型中，将吊重的摆动角度作为反馈信号，驱动力F作为输出信号。通过控制驱动力的变化控制小车的速度从而达到防摇的目的。图2表示系统的控制框图。

图2 仿真模型控制框图Fig.2 Simulation model control block diagram

3 MATLAB仿真及数据分析

通过MATLAB中的Simulink模块建立仿真模型。将仿真参数带入上述动力学方程可得出摆角运动状态。仿真参数由表1给出。

表1 仿真参数表Table 1 Simulation parameter table

本次仿真的工况为小车加速到0.17 m/s之后，让小车减速并停止。仿真分析包含4种情况。第一，当摆长为0.5 m时，撤掉驱动力小车由于阻力的原因自动停止，并观察吊重摆动角度的变化。第二，当摆长为0.5 m时，通过PID控制器控制小车的停止，并观察吊重摆动角度的变化。第三，当摆长为1 m时，撤掉驱动力小车由于阻力的原因自动停止，并观察吊重摆动角度的变化。第二，当摆长为1 m时，通过PID控制器控制小车的停止，并观察吊重摆动角度的变化。

3.1 摆长为0.5 m时的仿真结果

图3为吊重摆长为0.5 m时，小车由于阻尼的存在进行减速运动过程中吊重的摆动状态。图3表明吊重摆动的最大角度为0.08 rad，摆动角度随时间逐渐减小。在t=50 s时，摆角减小到0.04 rad。由图3可以看出，最大摆角的减小趋势接近线性。

图4为采用PID控制器之后吊重摆动角度的变化。最大摆角出现在第一次波谷，摆角大小约为0.05 rad。随着时间的增加，最大摆角大幅度减小，第二次波谷值为0.02 rad，相比第一次幅值减小了0.4倍。当t=7 s，吊重停止摆动，在7 s内吊重总共摆动了6次，前两次摆动幅度较大，之后摆角较小。7 s之后小车和吊重都停止摆动。

图3 摆长为0.5 m时吊重摆长自由停摆Fig.3 Free hanging of hoist(l=0.5 m)

图4 PID控制吊重摆角变化Fig.4 Change of hoist swing angle of PID control

3.2 摆长为1 m时的仿真结果

图5表明当撤去外力之后，吊重摆角最大为0.05 rad，50 s之后摆角减小到0.02 rad。在50 s内吊重总共摆动了31次，每次幅度逐渐减小。

图6表示在摆长为1 m的情况下，当恒定消失之后，通过控制器控制小车的停止及吊重摆动的变化。在控制器的作用下，吊重最大摆角出现在第一次波谷约为0.035 rad。出现第二次波谷时摆角相比第一次减小一半。吊重停摆的时长总共约为13 s，在此期间吊重摆动次数为8次。

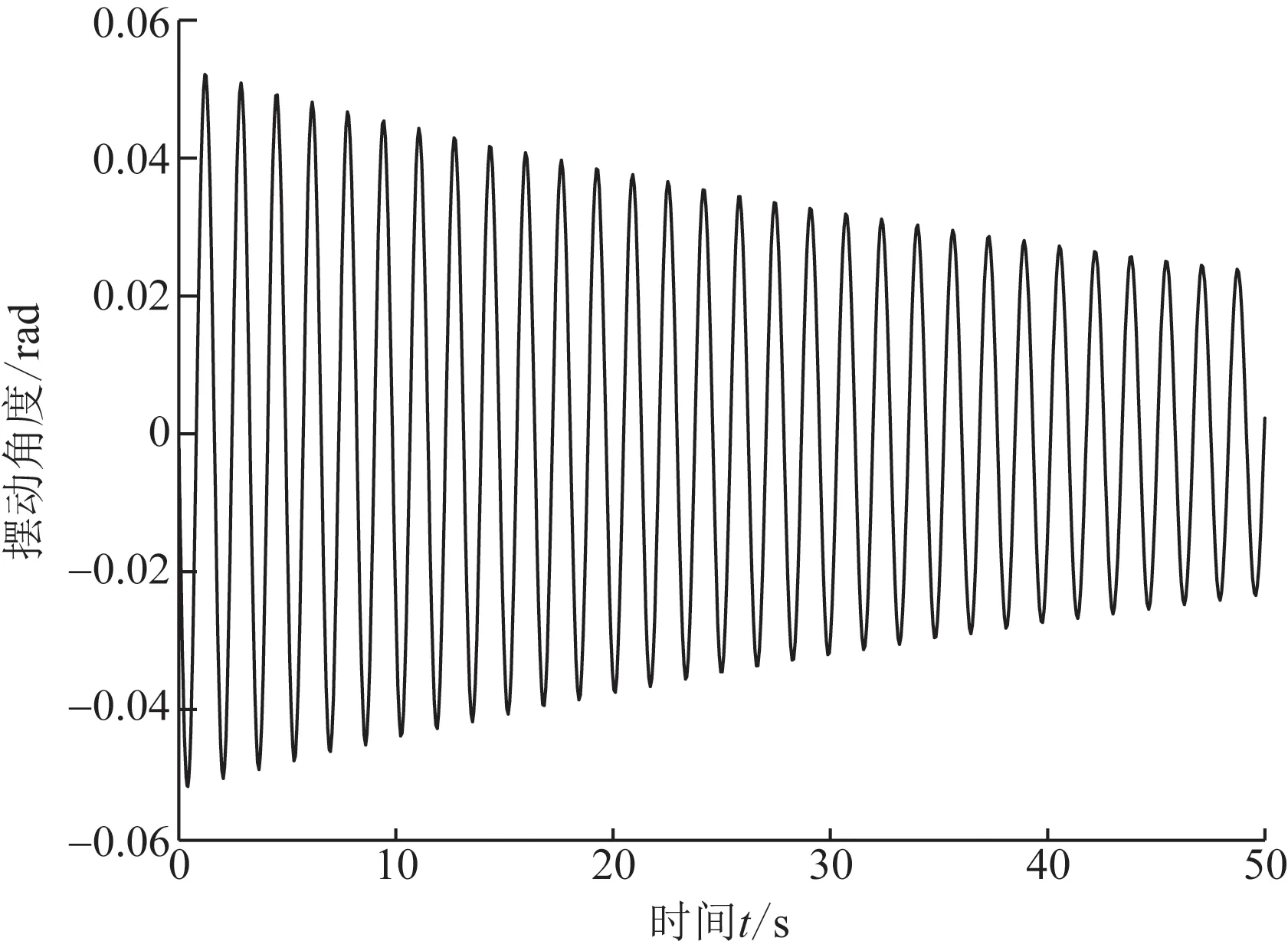
图5 摆长为1 m时吊重摆长自由停摆Fig.5 Free hanging of hoist(l=1 m)

图6 PID控制吊重摆角变化Fig.6 Change of hoist swing angle of PID control

3.3 仿真结果数据对比分析

通过仿真分析可以得出，当吊重摆长为0.5 m时，吊重自由停摆的角度最大为0.07 rad，吊重摆动周期约为0.9 s。当吊重摆长为1 m时，吊重自由停摆的角度最大为0.05 rad，吊重摆动周期约为0.7 s。吊重摆长越长，摆动角度越小，摆动周期越大。

在PID算法控制下，当摆长为0.5 m时，吊重停摆所需时间为7 s，最大摆角约为0.05 rad，摆动次数约为6次。当摆长为1 m时，吊重停摆所需时间为13 s，最大摆角约为0.035 rad，摆动次数约为8次。吊重摆长越长，在控制器的作用下，最大摆角越小；达到稳定状态的时间越长；停摆之前摆动的次数越多。

4 试验验证及数据分析

验证仿真结果的真实性，搭建简易的试验平台测量试验数据。试验平台主要由CPU，伺服电机，小车，吊重及编码器组成如图7所示。伺服电机提供小车的驱动力，编码器连接在吊重铰点上测量摆动角度。控制器CPU由STM32F103组成，CPU通过发出PWM波控制电机的转动，调节PWM波的频率可以调节电机的转速。CPU同时还可以实时采集编码器反馈的数据并将数据传输给上位机。进行防摇控制时，将采集的数据经过PID控制算法，改变电机转速从而达到防摇的目的。

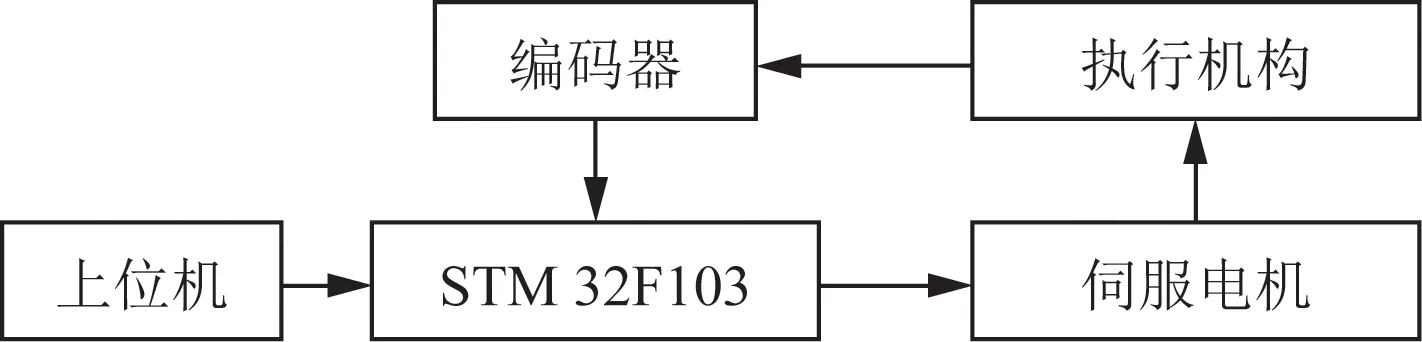
图7 试验台示意图Fig.7 Schematic diagram of test bench

4.1 摆长为0.5 m时的试验数据

图8为当摆长为0.5 m时，试验台自由停摆及防摇时的吊重摆动角度。曲线1为吊重自由停摆时的曲线图，其最大摆角约为8°，随着时间的增加，由于阻尼的存在摆角逐渐减小。当t=45 s时，摆动角度减小到1°，在此期间，吊重摆动了35次。在数据采集过程中因为存在干扰，故最大摆角存在一些波动。

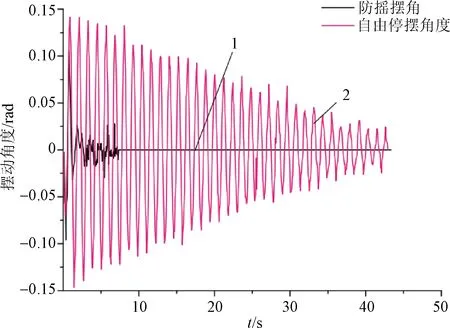
图8 摆长0.5 m试验数据Fig.8 Test data of pendulum length of 0.5 m

曲线2代表采用PID算法进行防摇控制的吊重摆动曲线图。加入控制算法之后，吊重最大摆角减小为6°。经过第一个周期之后，吊重的摆角快速降低为1.5°。在之后的5 s内吊重摆角逐渐减小到0。在防摇过程中，由于干扰的作用，摆角出现了3次奇异的波动。整个防摇过程大约用时7 s，相比于自由停摆大大缩短了时间。

4.2 摆长为1 m时的试验数据

图8为摆长1 m时吊重自由停摆和防摇停摆的试验对比图。曲线1为吊重自由停摆时的曲线图，其最大摆角约为6°，之后摆角逐渐 减小。当t=45 s时，摆动角度减小到4°，在此期间，吊重摆动了28次。

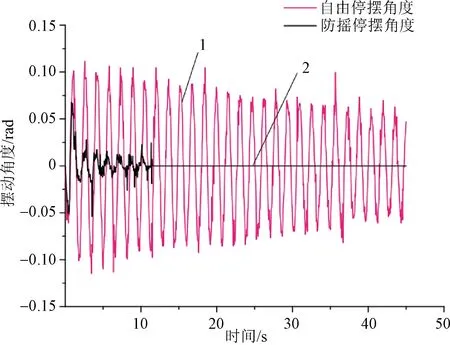
图9 摆长1 m试验数据Fig.9 Test data of pendulum length of 1 m

曲线2代表采用PID算法进行防摇控制的吊重摆动曲线图。加入控制算法之后，吊重最大摆角减小为4°。经过第一个周期之后，吊重的摆角快速降低为1.5°。整个防摇过程大约用时12 s。

4.3 试验结果对比分析

由试验数据可以看出，加入PID控制器可以有效的降低吊重的摆动角度，并且可以大大缩短吊重停摆所需的时间。吊重的摆长会影响吊重摆动的最大角度，摆动周期以及停摆的时间，同时当加入PID控制算法之后，会影响控制吊重停摆的时间。

5 结论

(1)起重机在停摆过程中，通过PID控制器可以有效的降低停摆过程所需的时间。

(2)增加摆长的长度可以有效的减小吊重的最大摆动角度。

(3)减小摆长的长度可以减小吊重自由停摆和防摇控制停摆的时间。

在起重机防摇应用中，应当根据实际情况合理调节吊重的摆长以适应工程当中的应用环境。

在接下来的工作中研究变绳长下，控制器参数自适应调整算法。通过该算法获得在满足工程应用的条件下，通过该算法可以实时整定控制器参数，从而有效的降低防摇控制时间及最小摆动角度。