基于邻域粗糙集和灰狼算法优化Elman的民航发动机滑油量预测

瞿红春，高鹏宇，朱伟华，许旺山，郭龙飞

(中国民航大学航空工程学院，天津 300300)

滑油系统的工作状态好坏直接影响着发动机的可靠性和安全性。先进的在线监测方法是滑油系统状态监控的研究热点，如滑油磨粒在线监测[1]、滑油的光谱分析[2]、滑油压差异常的诊断[3]、滑油黏度监测[4]、滑油消耗的预测[5-6]。针对滑油系统工作参数(如滑油量、滑油中金属屑含量)预测的研究较少。准确预测民航发动机滑油量可预防发动机在飞行过程中因滑油消耗量过大、滑油箱滑油量过少而发生报警甚至空中停车，对减少航空公司运营成本和保证飞行安全具有重要的意义。

发动机滑油量预测受飞行阶段和各阶段状态参数影响，属于高维参数预测问题，机器学习方法是一种解决途径。皮骏等[7]采用改进粒子群优化支持向量机的方法来预测发动机排气温度；张锦等[8]利用遗传算法优化灰色神经网络预测隧道变形；Sun等[9]基于天牛须算法优化神经网络来预测材料的抗压强度；李玉花等[10]通过卷积神经网络对电脑信号进行预测分类；Chen等[11]利用长短期记忆神经网络预测股价的变化趋势；传统优化算法在处理大规模样本数据时可能出现训练时间长、搜索能力差、陷入局部最优的缺陷；深度学习如卷积神经网络和长短期记忆神经网络预测时易出现过拟合的情况[12-13]，从而影响预测精度。

针对发动机滑油量预测的工程问题，提出基于邻域粗糙集和灰狼算法优化Elman的方法来预测滑油量。通过邻域粗糙集算法提取重要度高的工作阶段，并将其状态参数作为灰狼优化(grey wolf optimizer，GWO)-Elman模型的输入特征向量进行滑油量预测。并将本算法与传统优化算法进行对比，以验证预测模型的可行性和有效性。

1 民航发动机滑油系统的监控

民航发动机滑油系统的工作原理：滑油箱提供的滑油经过滑油滤进入到滑油泵中；再通过压力供油的方式将油通过主燃油/滑油热交换器(进行燃油加温和滑油散热)后,一部分滑油加到轴承和齿轮部件中，另一部分通过滑油热交换器后再供到轴承和齿轮部件中；在润滑部件中会有一部分富余的滑油和空气混合，将富余的油气回到回油泵中，通过滑油箱进口处的油气分离器将空气分离并排出，将富余的滑油回到滑油箱中。

通常滑油数据来自滑油报文，滑油报文来自对某同型号发动机从燃油活门打开到着陆时的滑油参数记录，针对不同的发动机工作阶段进行监测如图1所示。图1记录了航班燃油活门打开、初始慢车、水平滑行、起飞、爬升(爬升是每隔约3 km记录一次数据)、开始巡航(巡航阶段是每2 h记录一次数据)、巡航结束和着陆时的滑油数据。

预测滑油量，需要监控发动机工作状态下多个可能影响滑油量的特征参数，有滑油本身的状态：OOILQ(滑油量)、OOILP(滑油压力)、OOILT(滑油温度)；也可能有飞行条件的影响：PALT(压力高度)、Ma(飞行马赫数)；发动机温度会影响滑油消耗从而影响最后的滑油量，因此需要考虑影响发动机温度的T12(进气道温度)、T25(低压压气机出口温度)、TI(滑油进口温度)和TO(滑油出口温度)分别进行监控。各转动部件和反映发动机工作状态的参数：N1(低压转子转速)、N2(高压转子转速)、OOFDP(滑油滤压力差)、WF(燃油流量率)也会影响发动机的滑油消耗。一个工作阶段下相关状态参数记录如表1所示。

图1 某型发动机不同状态下的滑油量分布Fig.1 Distribution of lubricating oil quantity of an engine under different conditions

表1 状态参数记录表Table 1 State parameter record sheet

2 GWO-Elman神经网络的预测原理

2.1 Elman神经网络

Elman神经网络是在前馈式神经网络的隐含层中加了一个承接层，作为一个延时以达到记忆的目的；从而使系统具有动态映射的能力，增强了网络全局的稳定性，比前馈神经网络具有更强的计算能力，也能解决快速寻优的问题。网络的算法原理可表示为

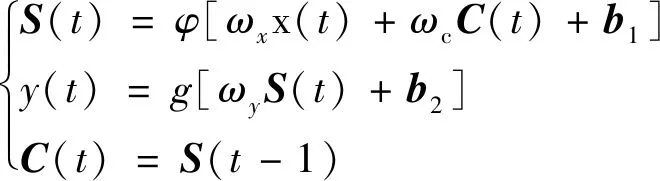
(1)

式(1)中：φ为输入层到隐含层的传递函数；x(t)为输入数据；g为隐含层到输出层的传递函数；t为迭代次数；S(t)为隐含层的输出结果；y(t)为输出层的输出结果；C(t)为承接层输出结果，ωx、ωy、ωc分别为输入层、隐含层和承接层的权重系数；b1、b2为隐含层及输出层的阈值[14]。

2.2 灰狼优化算法

单一的神经网络受到收敛速度和局部最优问题的限制，为此引入灰狼优化方法[15]。灰狼优化算法迭代寻优过程是模仿狼群狩猎的原理：每次迭代通过全局适应度最优的3只狼共同带领其他狼群向最优解靠拢，随着不断迭代使最优解更接近真实值，能够有效缓解收敛速度慢和陷入局部最优的问题。具体的狩猎过程分为以下步骤[16]：

步骤1计算种群中适应度最好的3只狼，分别标记为α、β、δ，其中α为等级最高的狼头，负责决策；第二等级β狼和第三等级δ狼负责协助α狼做出决策；GWO优化过程由这最优的3个解(α、β、δ指挥完成。

步骤2追捕并包围猎物。

D=CXp(t)-X(t)

(2)

X(t+1)=Xp(t)-AD

(3)

A=2ar1-a

(4)

C=2r2

(5)

式中：D为灰狼个体与猎物(实际解)的距离向量；Xp(t)为猎物的位置向量；X(t)为灰狼个体的位置向量；A和C为协同系数向量；a为收敛因子，在整个迭代过程a由2到0线性递减；r1和r2为[0,1]间的随机数。

步骤3伏击追捕猎物过程中，狼会根据猎物位置的改变而改变，再根据(α、β、δ)更新后的位置重新确定最优解，更新方程为

(6)

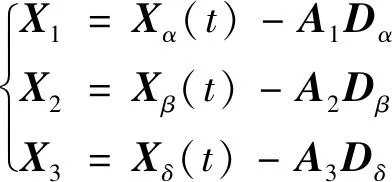
(7)

如图2所示，Dα、Dβ、Dδ是适应度最好的3只狼与候选狼之间的距离;Xα(t)、Xβ(t)和Xδ(t)分别为α、β和δ狼的位置向量;X(t)为当前候选狼群位置;X1、X2和X3分别为α狼、β狼和δ狼指引候选狼群更新后候选狼群的位置向量;X(t+1)为下一时刻灰狼群的位置向量。

图2 灰狼优化原理图 Fig.2 Schematic diagram of gray wolf optimization

步骤4捕获逃脱的猎物：实现过程通过式(3)实现，随着不断迭代，狼群与猎物的距离递减，对灰狼个体的平均适应度要求不断降低，如图3所示；同时A的绝对值不断递减，当A绝对值小于1时，表明狼在不断接近猎物，直至找到最优解。

图3 平均适应度随迭代次数变化Fig.3 Average fitness changes with the number of iterations

2.3 滑油量预测流程

由于着陆时发动机的滑油量比巡航阶段低，因此，通过输入开始巡航前的工作状态预测在着陆时的滑油量，保证在飞行中发动机的滑油量不低过正常值，预测流程如图4所示。

预测滑油量的具体步骤如下：①获取原始滑油数据，并进行归一化；②滑油数据预处理：分析数据，确定特征参数提取方法(同一参数不同飞行阶段之差)；③邻域粗糙集计算各个工作阶段重要度，比较不同半径结果下的拟合效果；④建立Elman网络，初始化误差容限、训练次数和学习率等网络参数；⑤数据输入到GWO-Elman神经网络，灰狼优化部分通过位置最好的3个解带领其他粒子向最优解靠拢；⑥通过不断迭代，不断更新适应度值和最优解位置来优化Elman网络中的权值和阈值，直到当A绝对值小于1时，表明最优解在不断接近实际值，直到找到最优解。

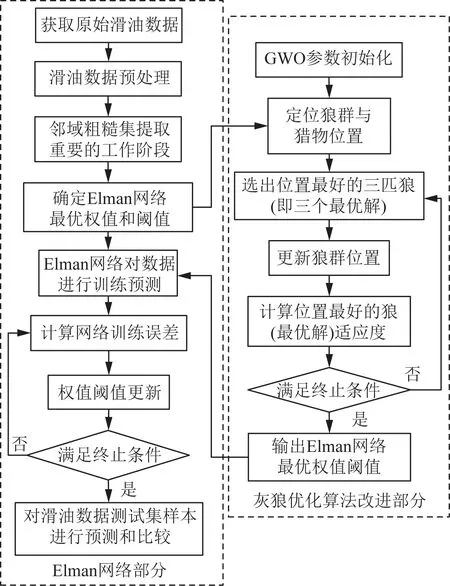
图4 滑油量预测流程图Fig.4 Flow chart of oil prediction

3 基于NRS-GWO-ENN预测滑油量

3.1 选取特征工作阶段

采用邻域粗糙集计算开始巡航(begin cruise)前各工作阶段相对于滑油量的重要度；其中邻域半径R用来划分样本特征的邻域指标，重要度是指特征向量在邻域指标以内对决策向量的影响大小，如表2所示。

表2 不同邻域半径下的工作阶段重要度Table 2 Importance of work stage under different neighborhood radius

表2所示，在不同邻域半径下对工作阶段的重要度计算结果分为以下三类：全部输入、去除taxiout-idle输入、选取take off-taxiout、climb3k-takeoff、begin cruise-climb6 k输入；对比精度和稳定性，如表3所示。

由表3可知，选取Take off-taxiout、climb10-takeoff、begin cruise-climb20工作阶段时，由于优化了输入参数的矩阵维度，提取出影响度高的工作阶段，去除重要度低的干扰特征向量，使结果拟合精度更高，稳定性更好；各点精度和绝对误差如图5所示。

表3 不同工作阶段提取的结果比较Table 3 Comparison of extraction results in different work stages

3.2 优化算法比较

其他优化算法中粒子群优化算法(particle swarm optimization,PSO)具有记忆性(粒子群体的历史最好解记忆传递给其他粒子)，调整参数少，结构简单，易实现等优点；但由于缺乏速度的动态调节，存在收敛精度低，存在局部最优的问题。遗传优化算法(genetic algorithm，GA)具有较强的鲁棒性，算法独立于求解域等优点；但由于是单一的遗传算法编码，存在收敛速度慢，效率低于其他优化算法，局部搜索能力差，求解结果强烈依赖于初始值的问题。为解决上述问题，引入灰狼算法并将拟合结果与上述传统优化算法进行比较，对比如图6所示。

图5 GWO-Elman预测滑油量精度和绝对误差Fig.5 Accuracy and absolute error of GWO Elman oil prediction

由于灰狼算法是模拟狼群的社会等级制度，每次迭代通过3个最优解带领其他解向真实值靠拢并保存最优解；自适应参数α保证了全局和局部的优化；可调整参数少收敛速度较快；可解决其他优化算法的部分缺陷。如图6所示，通过精度对比图可发现GWO-ENN精度最高，稳定性最好。不同优化算法下的精度与标准差对比如表4所示。

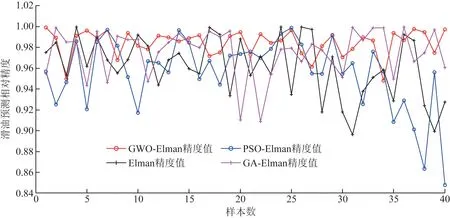
图6 不同优化算法拟合精度对比Fig.6 Comparison of fitting accuracy of different optimization algorithms

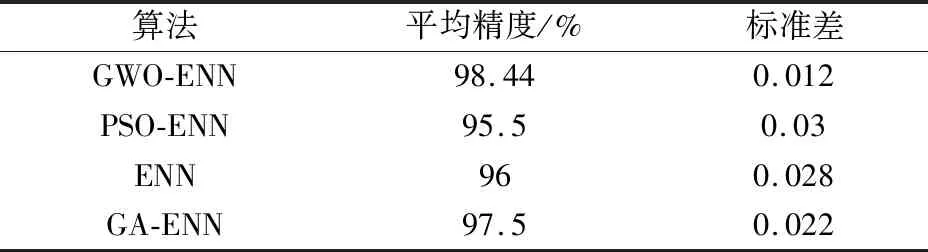
表4 不同优化算法下的拟合结果Table 4 Fitting results under different optimization algorithms

4 结论

提出邻域粗糙集与GWO优化ENN相结合的方法预测发动机在着陆时的滑油量。并分别与PSO-ENN、ENN、GA-ENN比较，证明GWO-ENN在精度和稳定性上的优势。预测结果表明：平均精度为98.44%，平均绝对误差为0.4，标准差为0.012。得出如下结论。

(1)提取特征参数时，通过比较，采用相邻工作阶段特征参数取差值的提取方法，能够反映飞行过程中发动机工作状态的动态变化。

(2)提取特征工作阶段时，有多种收敛半径下的重要度提取结果，通过比较预测滑油量时的拟合精度，最后确定选取水平滑行-起飞、爬升至10 km-水平滑行、开始巡航-爬升至20 km这3个特征飞行阶段。

(3)灰狼优化算法具有基础参数少，易于编程的特点，每次迭代通过3个全局适应度最优的解带领其他目标值向真实值靠近，避免单一神经网络和其他优化算法容易陷入局部最优的问题。

采用GWO-ENN方法面临着对高维参数提取特征时效果不如深度学习的问题。下一步工作可以试用循环神经网络(recurrent neural network,RNN)的方法，循环神经网络通常是将多个单元集成在一个时序模块里，预测滑油量可能会有更好的效果和改进。