面向全方案空间的装备体系任务现状分析方法研究

高思思，杨欣河，靳 捷，王家胜

(中国航天系统科学与工程研究院,北京 100048)

美国国防高级研究计划局(DARPA)在2017年提出了一种新的作战概念——“马赛克战”(Mosaic Warfare)，其核心思想是分解各种作战功能要素，通过低成本、低复杂度系统的快速、灵活组合与协同作战，实时响应多种威胁场景下的作战能力需求，形成非线性作战效果网，从而加重敌方的认知负担，形成不对称优势[1-3]。显然，随着未来战争形态向信息化条件下的高技术战争持续转变，作战要素之间的互联互通互操作变得越来越广泛、直接和高效，体系结构的复杂性随之增加。结构决定功能，越来越复杂的体系结构，意味着作战能力的生成方式多种多样，同样的装备体系能力水平，可由不同的作战要素按照不同的作战概念进行灵活组合来达到，未来的能力生成方式将更加灵活。

由于作战能力可依据不同的作战概念分解成多种作战活动序列来实现，每个作战活动可由不同的作战要素完成，当作战活动序列较长、作战要素选择较多时，生成能力的装备体系方案空间将呈指数级增长，常以亿为单位。此时要对装备体系作战能力进行评估，需要对巨大的方案空间进行计算和筛选，传统的仿真评估方法适用性较差。

中国在进行装备体系能力现状分析以确定能力缺口时，一般以典型场景样式下的典型装备体系方案基础，评估出的效能现状取决于典型装备方案的选择。然而，装备体系方案的典型标准是什么，并没有明确给出，这使得现状分析过程中存在很强的主观性[4-8]。以Joseph V为主的国外学者认为典型装备体系方案应该基于对某任务条件下的全方案空间探索来得出，并在此观点的基础上提出了通过RAAM(rapid architecture alternative modeling)框架给出了构建全方案空间的架构模型和分布式算法，但该方法仅解决了全方案空间的构建和快速计算问题，而对于典型方案的确定，还需要人工进行筛选。在该研究中，筛选的标准也并没有给出[9]。

在进化算法(evolutionary algorithms,EAs)方面，自Schaffer提出用EA解决多目标规划问题以来，多目标进化算法成为热门的研究领域，各位学者提出了大量的高效算法，现在比较常用的基于Pareto支配的多目标进化算法有NSGAⅡ、SPEA2和NPGA2等，这些算法在求解2、3目标规划问题中都具有很好的收敛性和多样性，但是在3目标以上的高维多目标规划问题(MaOPs)中，由于复杂度的增加，Pareto支配关系在高维空间基本失效，选择压力变小，算法的性能无法达到理想的效果[10-11]。显然，现有改进算法在求解高维多目标优化时很难同时满足多样性和收敛性。

为满足未来战争的作战需求，并避免现有装备体系分析方法中存在的客观性问题，现借鉴马赛克战的作战理念，构建可完成作战任务的装备体系全方案空间，为评估现有装备体系完成作战任务的效能水平提供基础。同时由于武器装备体系方案的评价指标的数量一般在3个以上，为了保证探索装备体系方案空间时保证解集的收敛性和多样性，针对武器装备体系方案评估问题，基于现有改进算法中存在的缺陷，在NSGAⅡ中引入自适应交叉算子进行改进，使得筛选出的方案集合能最大精度地代表装备体系的能力现状，从而为装备体系能力现状分析提供一套完整、灵活的分析方法，以牵引装备体系的发展与建设。

1 面向全方案空间的装备体系任务现状分析框架

为全面客观地评估装备体系战斗力现状，以战术级作战任务为研究对象，作战任务可以由作战要素直接完成。以作战概念、任务-系统的映射为外部输入，建立任务层次结构、定义任务指标体系，构建作战任务的装备体系全方案空间，以便于探索全方案空间进行装备体系战斗力评估。

借鉴RAAM方法，根据作战概念将作战任务分解成若干个作战活动，创建任务层次矩阵。每个作战活动可由单一的武器系统完成，通过建立任务指标体系，可度量装备系统完成作战活动的效果。而C4ISR为各武器系统之间的互联互通提供了条件，根据任务-系统的有效映射，通过为每个作战活动选择实现的装备系统，得到的装备系统组合便代表可完成作战任务的装备体系方案。由于装备系统功能的多样性，使得每个作战活动的可选装备系统不只一个，所以作战任务的实现方式非常多，但通过系统与作战活动的组合分配，可枚举出完成作战任务的所有装备体系方案。最后以最优化各方案的任务指标为目标，利用遗传算法对全方案筛选，快速生成代表战斗力现状的装备体系方案集，从而客观高效地确定能力缺口。具体分析框架如图1所示。

2 装备体系备选方案空间的构建

2.1 创建任务层次结构

在确定实现能力需求的战术级作战任务后，首先根据相关作战概念进行任务分解，创建任务层次结构。任务层次结构的主要任务是提供能力需求的作战任务，隶属于主要任务的是完成主要任务所需的各种任务，这些任务均可以进一步分解，直到各子任务可以由某一武器系统单独完成或实现，从而得到一系列作战活动序列。根据不同作战概念分解得到的任务层次结构是不一样的。如图2所示，实线代表分解，虚线代表权衡，在对主要任务进行分解时，根据不同的作战概念，子任务2可以分解为任务3、任务4和任务5，也可以分解为任务6和任务7，从而得到的完成主要任务的作战活动序列可以是{1，3，4，5}，也可以是{1，6，7}。

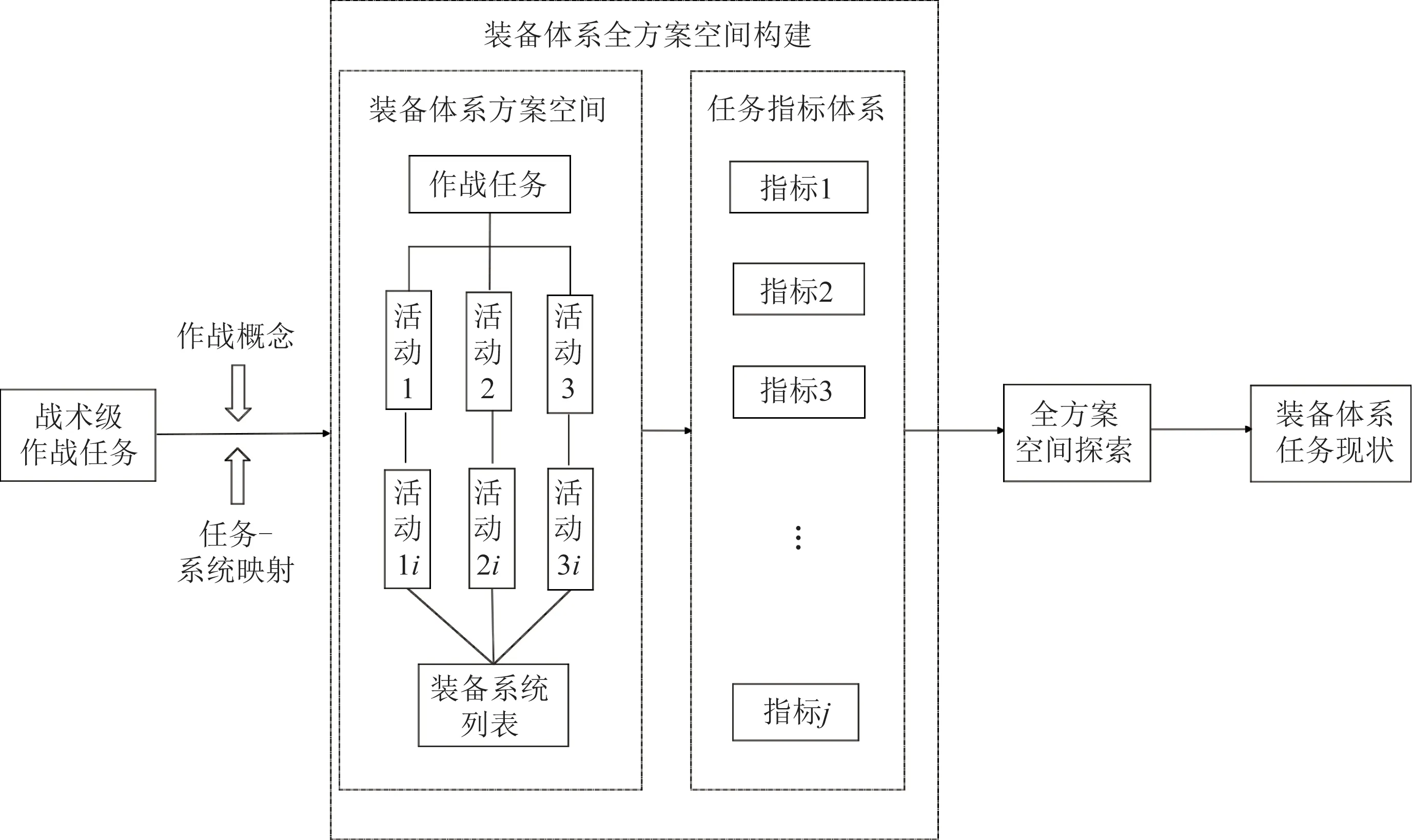
图1 面向全方案空间的装备体系任务现状分析方法研究框架Fig.1 The framework of research on analysis method of the task status of the equipment system oriented to the solution-wide space

图2 任务层次结构及任务-系统映射Fig.2 Hierarchy of task and task-system mapping

任务层次结构是完成一项能力所需任务的层次结构描述。通过描述能力层次结构，以便于描述整个体系备选方案空间。在这一阶段，为度量装备系统完成各作战活动的效果，还需建立任务指标体系，图2中假设作战任务的任务指标分别为指标A和指标B。每个任务-系统配对的任务指标值是根据各武器系统的战技指标，在各作战活动面临的威胁和所处环境条件下，通过仿真或历史数据计算出的武器系统执行其能承担的作战活动的水平。常见的任务指标有：成功率，完成时间、复杂度和可维护性等。

2.2 构建装备体系备选方案空间

在创建任务层次结构之后，挑选出可完成作战活动的所有武器装备系统，每个装备系统能够完成任务层次结构中的一个或多个作战活动，每个作战活动也可能由多个系统单独完成，具体映射如图2所示。在任务层次结构及系统到任务的有效映射的基础上，通过为每个作战活动分配装备系统，通过不同的分配组合便可枚举出所有可完成作战任务的装备体系方案。在图2中，首先通过选择完成子任务2的作战活动，再选择完成作战活动的系统，在进行两次决策后可以枚举出所有可行的装备体系备选方案，图2中主要任务的全方案空间包括10种方案，具体如表1所示，其中STi表示子任务i，Sj表示武器系统j。

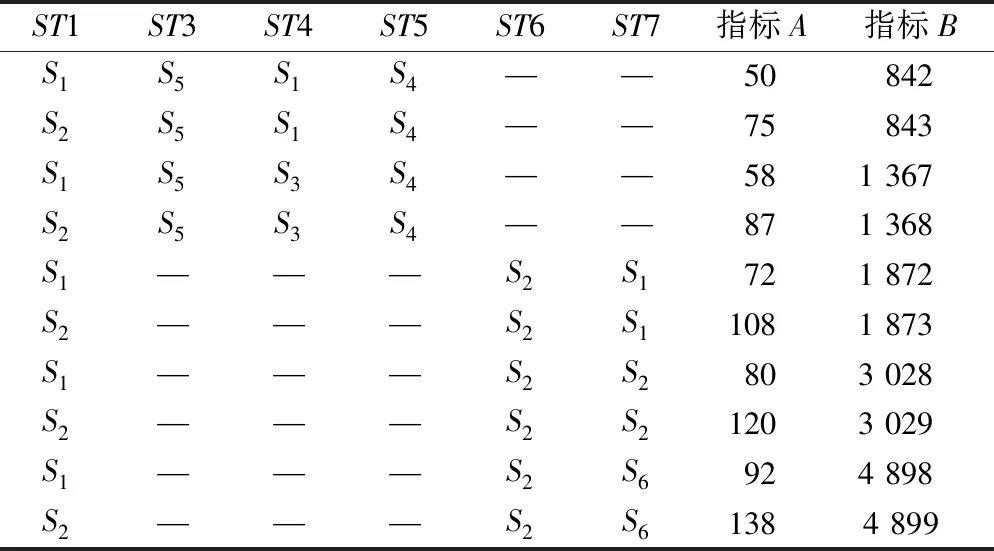
表1 作战任务全方案空间Table 1 The solution-wide space of combat missions

2.3 定义聚合算子

上述任务指标A和B仅能够衡量每个装备系统完成作战活动的效果，为衡量每个装备体系方案完成作战任务的效果，确定完成装备体系任务能力现状，根据作战活动序列结构及作战活动之间的关系，针对每个任务指标建立聚合算子。通过聚合算子可以衡量每个装备体系方案完成作战任务的优劣程度，以支持装备体系任务能力现状分析。

假设根据作战活动之间的关系，指标A和B的聚合算子分别为：

(1)

(2)

式中：A1、B1和A2、B2分别代表任务1和任务2的完成效果，i=3,4,5或6,7。选取图2中的一个方案组合{1,3,4,5}为例，该方案的任务指标分别如下：A=2×(5+7+13)=50，B=2+(5×8×21)=842。其余方案的聚合指标值见表1。

通过构建作战任务的装备体系方案空间，得到了可完成作战任务的全部方案以及任务指标聚合算子。但由于作战任务可由不同的作战活动序列完成，每个作战活动都可由不同的武器系统完成，当作战活动序列较长、可完成作战活动的系统较多时，完成任务的方案空间将呈指数级增长，常以亿为单位。此时要计算出每个方案的任务指标值再进行筛选以确定能力现状是难以实现的，并且是无意义的。同时每个方案的各个任务指标往往是相互冲突的，照顾了一个度量指标的“利益”，必然导致其他至少一个度量指标的“利益”受到损失，从而为获得装备体系任务现状而对全方案空间进行探索实际上是一个拥有巨大可行域的多目标规划问题。针对一个多目标规划问题不存在一个绝对的或者唯一的最好解，而是存在一个Pareto最优解集。对于装备体系能力现状而言，多个任务指标之间一般而言也是“此消彼长”的关系，难以找到一个最好的方案使得所有任务指标均优于其他所有方案，因此装备体系任务现状也是一个集合。

3 基于改进NSGAⅡ的全方案空间探索

目前，求解多目标规划问题主要有两类方法：传统数学规划方法和多目标智能优化算法。传统求解多目标规划问题的数学规划方法，如多目标加权法，约束法等，无法收敛到Pareto最优前沿面。多目标智能优化算法包括遗传算法、粒子群算法、蚁群算法等，但粒子群算法与蚁群算法主要应用于连续问题的求解，无法有效解决离散及组合优化的问题，因此本文选取多目标遗传算法来探索全方案空间。

Deb等[12]在2000年提出非支配排序遗传算法Ⅱ(NSGA-Ⅱ)求解多目标规划问题，通过在每一代进化时构造当前进化群体的非支配集(即当前进化群体的最优个体集合)，并通过最优个体保留机制，使每一代所构造的非支配集不断地逼近真正的Pareto最优边界实现，该方法具有运行速度快、鲁棒性好、收敛性好等优点。但NSGAⅡ使用固定的交叉概率和变异概率，而进化概率的选择对算法的有效性具有极大的影响，不合理的进化概率参数设定，不仅可能导致算法的收敛性、搜索速度下降，还可能导致算法陷入局部最优。

现借鉴文献[13]提出的自适应交叉算子和变异算子来有效避免上述问题，以每个度量指标的聚合算子为目标函数，以系统-子任务的度量指标为数据输入，使用改进的非支配排序遗传算法寻找全方案空间中的Pareto最优方案集，确保得到的方案集合为全局最优。下面将按NSGAⅡ的运算流程介绍其进行全方案空间探索的步骤。

3.1 编码与解码

编码的设计是使用遗传算法解决实际问题中极为关键的要素，通过编码将实际问题的解空间映射到编码空间，本文采用整数编码方式[14-16]。假设根据某一作战概念，某作战任务可分解为具有N个作战活动的作战活动序列，每个作战活动可由ni个武器系统完成(编号均记作0,1,…,ni-1)，Sij表示可完成作战活动i的系统j，j∈{0,1,…,ni-1}。为将该作战任务的方案空间映射到编码空间，每个方案由[ST1,ST2,…，STi,…,STN]的形式表示，STi表示作战活动i，则每个STi的取值可在{0，1，…，ni-1}中选择，其对应的取值便代表作战活动可选的武器系统编号。

图3 染色体编码与解码示例Fig.3 Example of chromosome encoding and decoding

解码过程是从编码到各个度量指标值的映射，以度量指标时间T和成功概率P为例，T(1,1)表示作战活动1由系统S11执行的完成时间，P(3,3)表示作战活动3由系统S33执行的成功概率。

3.2 种群初始化

使每个作战活动在其取值内随机选取，通过N个作战活动选取的不同装备组合形成H个不同的备选方案，得到规模大小为H的初始父代种群P0。

3.3 自适应进化算子

通过交叉操作与变异操作对初始种群进行进化，可以得到新的备选方案，产生新的子代种群Qt。交叉是从Pt中随机选取出不同方案，对不同方案中某一个或者几个相同的作战活动的取值进行交换，其他的作战活动取值维持不变，从而形成新的方案。变异则是对某一方案中的某一作战活动的取值进行改变，其他作战活动的取值也保持不变，而形成新的方案。通过交叉和变异，使得种群中方案的分布性和多样性增加，使得算法能够更好的探索全方案空间。现使用自适应交叉算子和变异算子进行进化，具体的自适应交叉概率pc和变异概率pm分别为

(3)

(4)

式中：pmax、pmin为最大、最小交叉/变异调节参数；fmax为当前种群方案中最大的适应度值；favg是所有种群方案适应度值的平均值；f1为交叉/变异方案的适应度值；t代表当前的进化代数，gen为算法进化的总代数[17]。采用上述自适应进化算子可使得在进化前期进化概率较高，增加种群的多样性，提高了算法的搜索能力，避免了陷入局部最优，可使得Pareto最优方案集更接近真实前沿。随着进化代数的增大，进化概率逐步降低，不仅增加了算法的灵敏度，还保证了算法的收敛性。

3.4 Pareto排序

父代种群Pt在进行上述进化操作后，形成新的子代种群Qt，为从集合Pt∪Qt选择出H个优秀的备选方案组成新的父代种群Pt+1，需要对Pt∪Qt中的所有方案进行优先级分层。根据方案的支配关系，采用快速非支配排序算法将Pt∪Qt分成F1，F2，F3，…[18-19]。

3.5 精英保留策略

为维持多目标优化群体的分布性，采用锦标赛选择机制，优先选择非支配排序中优先级高的方案，当方案等级相同时，计算方案的拥挤距离，选择拥挤距离较大的方案。具体选择步骤为对Rt=Pt∪Qt(种群大小为2H)进行Pareto排序，同时找出位于临界层。处于临界层之前的方案全部保留到下一代，而位于临界层的方案则计算其拥挤距离，根据拥挤距离从大到小的顺序选择若干方案保留到下一代，直至新一代种群的方案数目为H[20-24]。具体如图4所示。

图4 NSGA-II新一代种群生成过程示意图Fig.4 Schematic diagram of the generate process of NSGA-II new population

通过引入自适应进化算子不仅保持了种群的分布性，还保证了种群的多样性，解决了算法提前收敛的问题，使得算法得到的Pareto最优方案更接近真实的Pareto边界。

初始方案种群通过上述的进化、选择迭代演化，当满足终止条件后，种群中的方案为可实现作战任务的Pareto 最优方案集合，决策者可以根据实际情况或偏好从中挑选出符合要求的方案代表能力现状。NSGAⅡ算法的求解流程图如图5所示。

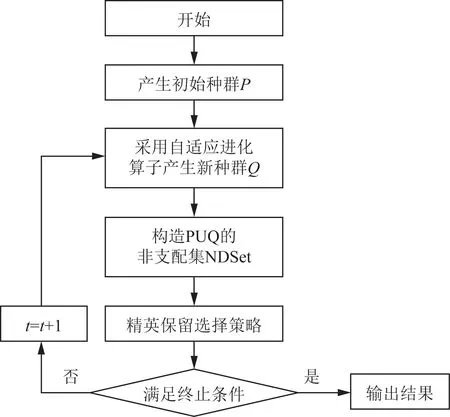
图5 自适应进化算子的NSGAⅡ算法流程图Fig.5 Flow chart of NSGAⅡwith adaptive evolution operator

4 案例分析

获取和保持空中优势是实现威慑制止或击败敌方的战略目标的行动之一，为完成该行动需要实现肃清空域、压制防空和制空突击等作战目标。

压制防空(SEAD)是指通过破坏性和或毁灭性武器中和、破坏或暂时削弱敌方地面防空系统的活动。地面防空系统一般包括交战系统、传感器系统以及控制指挥网络。交战系统包括地空导弹(SAM)和防空炮兵(AAA)，早期的预警和火力控制雷达通常用作传感器系统，这些武器系统的组合被称为综合防空系统(IADS)。

4.1 SEAD任务分解

对SEAD这一作战目标进行分析，构建武器装备体系消除敌方综合防空系统(IADS)实现SEAD。借鉴SEAD的作战概念，可以将任务分解为探测、识别、跟踪、目标分配以及火力打击五个作战任务序列。再根据相应的作战条令，五个作战活动序列可以进一步分解为作战活动序列1.1，1.2，…，5.4，具体如表2所示。

4.2 构建SEAD备选方案空间

为完成上述作战活动序列，挑选出可执行活动序列的所有武器系统，并确定各武器系统能够承担的作战活动，这些系统包括CVN、Central C2、…、SOF，记录有效的系统-任务配对，可形成完成压制防空任务的完整装备体系备选方案空间，具体如表2所示。根据任务层次结果及映射关系可发现，SEAD任务存在6亿4千多万个装备体系方案，要对所有方案计算任务指标值再进行筛选需要大量的时间，并且是无意义的。

表2 SEAD子任务-系统映射Table 2 Task-system mapping of SEAD

在SEAD任务中，装备系统完成任务程度的度量指标包括成功概率P、复杂性度C、完成时间T和可维护性M。系统执行某一任务的度量指标得分由主题专家或计算机仿真给出。

4.3 定义度量指标聚合算子

为衡量每个方案组合完成SEAD任务的效果，需要建立聚合算子，计算每个方案的任务指标值。

根据作战活动序列，SEAD任务的任务指标成功概率P的聚合算子为

P=∏Pij

(5)

式(5)中：Pij表示武器系统j执行作战活动i时的成功概率。

复杂度C是对完成SEAD任务所需作战活动的复杂度的总体估计，每个系统到任务映射的复杂度指标值均对总体复杂度指标值产生影响。复杂度C的聚合算子为

C=∏C1C2C3C4C5

(6)

(7)

C2=C7j

C3=maxCij，i=8,9,10

(8)

C4=minCij，i=11,12,13

(9)

(10)

式中：C1、C2、C3、C4和C5分别表示探测、识别、跟踪、目标分配以及火力打击5个作战任务序列的复杂度；Cij表示武器系统j执行作战活动i时的复杂度。

完成时间T是完成SEAD任务的总时间，在执行SEAD任务时，必须以串行方式完成所有作战活动序列，因此完成的总时间T是各系统完成作战活动所需时间的总和，即

T=∑Tij

(11)

式(1)中：Tij表示武器系统j完成作战活动i时的时间。

可维护性M描述了SEAD任务的总体可维护性，随着系统的使用，它们会损耗并需要进行维护。可维护性M是完成SEAD任务的一组装备系统完成作战活动中最低的可维护性Mij，即

M=minMij

(12)

式(12)中：Mij表示完成作战活动i的武器系统j的可维护性。

4.4 SEAD方案空间探索

为确定能力现状，现对SEAD任务的全方案空间进行探索寻优。在SEAD任务中需要同时进行优化的目标函数如下：

f1=maxP

(13)

f2=minC

(14)

f3=minT

(15)

f4=maxM

(16)

为保证使用自适应进化算子NSGAⅡ算法求解的Pareto解集的有效性，以反映算法收敛性及分布性的超体积评价指标(hypervolume，HV)为评价标准，测试不同的种群规模大小、进化概率范围以及最大迭代次数时HV指标值。通过先固定进化概率及迭代次数，选择不同的种群规模分别运行30次，记录HV指标值，发现种群规模H过大时算法的收敛性与稳定性较差，规模过小时多样性较差，选择种群规模H=50时HV指标表现最优；固定种群规模H=50以及变异概率、迭代次数，选取不同的变异概率范围[0.2,0.9]、[0.4，0.9]、[0.6，0.9]以及[0.8，0.9]，发现交叉概率的取值较大时，其收敛性及稳定性也较差，测试确定pcmax=0.9，pcmin=0.2；按照上述过程，依次确定变异概率的范围及迭代次数，最后通过测试选取种群规模H=50，pcmax=0.9，pcmin=0.2，pmmax=0.4，pmmin=0.2，gen=500，此时算法具有较好的收敛性及分布性，求得的Pareto最优解集能更好地贴近能力现状。

现根据任务-系统的各个任务指标值，在Python环境下实现改进的NSGAⅡ求解上述多目标规划问题。由于4个目标同时优化时，Pareto的解集构成一个超曲面，无法用图直观地显示可行解，表3给出了一次运行中得到的20个Pareto最优解。决策者可以根据实际情况、偏好等从Pareto解集中选择装备体系方案代表装备体系任务现状。

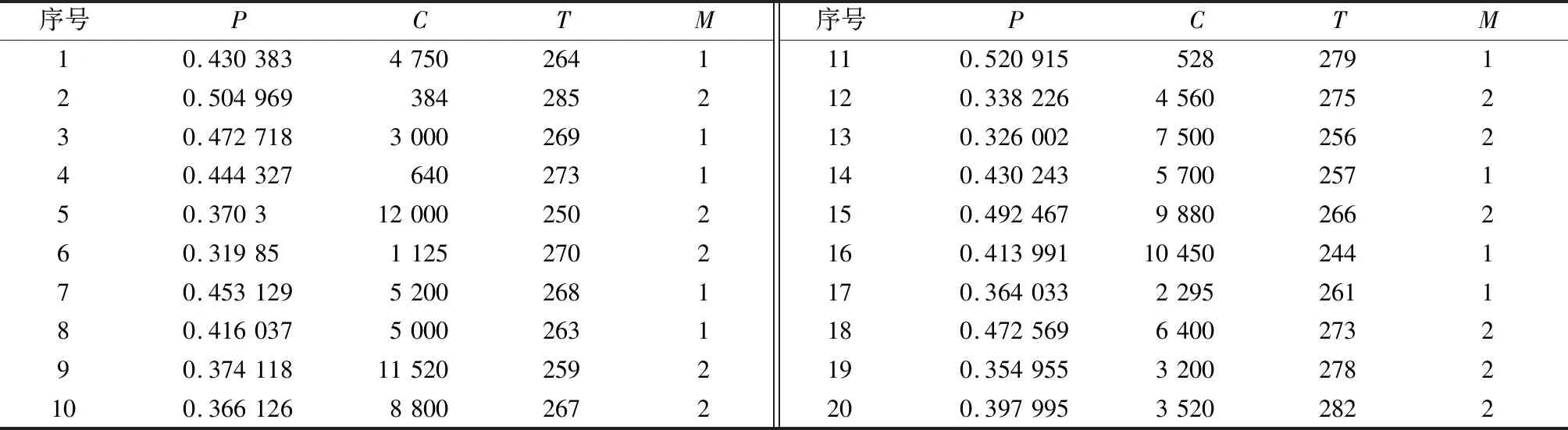
表3 Pareto解集/装备体系任务现状Table 3 Pareto solution set/task status of the equipment system

显然，利用改进的NSGAⅡ对SEAD任务包含6亿4千多万个方案的装备体系方案进行快速生成和筛选，不仅避免了传统装备体系任务现状评估方法使用典型装备体系方案造成的主观性，极大的提高装备体系任务现状分析的客观性，而且该评估方法具有较强的通用性，可广泛用于各类军种装备的评估。

5 结论

(1)通过对作战任务建立的任务层次结构，及进行子任务和系统组合配对，简洁高效地构建出完成作战任务的完整可行方案空间，以便于在能力分析时探索全方案空间。

(2)针对方案空间巨大、度量指标相互制约的问题，提出基于NSGAⅡ进行方案空间的自动探索筛选，并引入自适应进化算子，保证算法求解的有效性，使得Pareto最优解集能精准地反映装备体系任务现状。

(3)运用提出的方案空间构建方法及求解算法对“压制防空”任务进行装备体系任务现状分析，证实了方法及算法的高效性，提高了国内在装备体系任务现状定量分析方面的客观性。以后的研究进一步考虑对作战活动和武器系统的执行约束，使得方法更贴合实际问题具有更强的应用价值。