煤矿起重机吊重防摆控制研究

张桂欣， 胡相捧， 李雪伟

（1.中煤科工集团 国际工程有限公司,北京100013；2.中国矿业大学（北京）机电与信息工程学院，北京100083；3.河南能源化工集团 重型装备有限公司，河南 开封475004）

0 引 言

煤矿井下设备不仅种类多，而且形状和质量各异，在井下利用起重机进行设备的起吊和安装时，也面临类似于港口码头起吊作业时重物的摆动问题。很多学者采用不同的控制方法对起重机消摆进行了研究，例如，采用经典的PID控制或模糊控制、神经网络等智能控制方法[1-7]。在起吊运行过程中如果考虑吊重提升运动，其摆振模型是一个非常复杂的非线性问题，大多数学者都把摆振非线性模型简化为线性方程进行防摆控制研究，也有学者对摆振非线性模型进行智能控制的研究。即使个别研究者考虑了吊重提升运动对摆振的影响，但也没有考虑到通过提升电动机来实现吊重的消摆。本文基于井下作业空间的限制，起重的高度往往不会像地面那么高，在考虑绳长变化的条件下建立起重机吊重的摆振模型，运用非线性振动理论求得吊重摆角的解析表达式，然后采用MATLAB的Simulink工具进行仿真。结果显示，起吊重物时通过控制绳长能够很好地控制吊重的摆动。

1 数学模型的建立

建立吊重摆振数学模型时基于以下假设：1）缆绳的质量相对于抓斗及重物的质量可忽略不计, 缆绳的刚度足够大；2）吊重与缆绳运行过程中所受阻力不计。

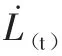
代入上面的加速度表达式得吊重摆动的数学表达式[8]：

2 方程的近似解

式（2）和荡秋千的数学模型相似，由经验可知，在秋千最大摆角处突然下蹲和平衡位置处突然起立会使秋千越荡越高，对起重机的摆振模型我们采用逆向思维，即采用相反的处理过程，在吊重最大摆角处突然提升重物和平衡位置处突然下放重物[9-10]。为此，设摆长的变化式[11]为：

令式（3）的解为

其中振幅A和相位φ均是时间t的慢变函数，令函数

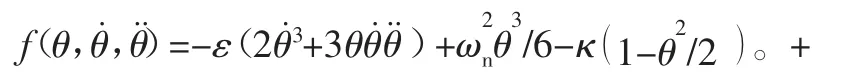
依据慢变振幅和相位法[12]有：

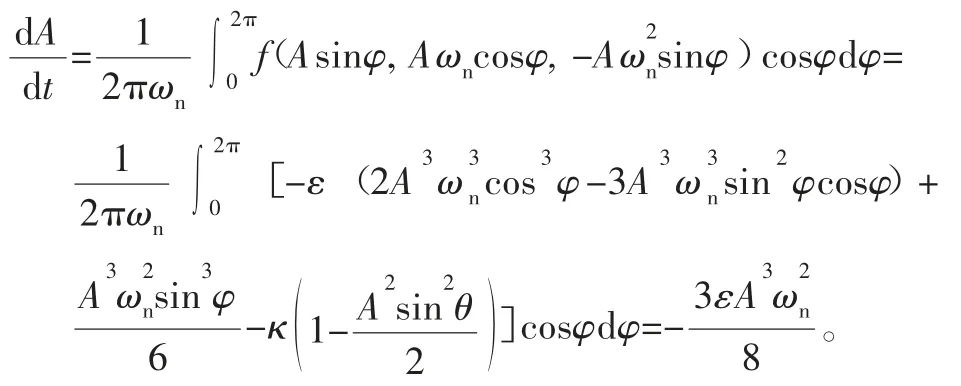
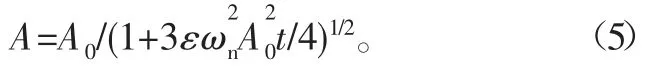
同理可求得：

把式（4）代入上式，并设φ（t=0）=φ0，积分求得：

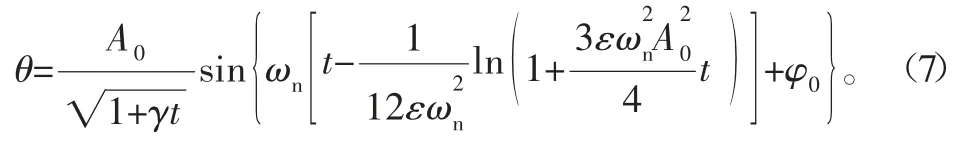
3 数值模拟及仿真

使用MATLAB的Simulink仿真工具对上述吊重摆振模型进行仿真[8]，仿真模型如图2所示。当起重机小车加速度分别为0、2、-5时的吊重摆振曲线如图3～图5所示。

从图3～图5可以看出，在不考虑阻尼情况下，当加速度等于0时，吊重做等幅振荡，当有加速度时，吊重也做等幅振荡，但动态平衡位置发生了变化，图4表示a=2时吊重在平衡位置θ=-0.2 rad处做等幅振荡。从能量角度解释这是合理的，不考虑阻尼，表明系统没有能量损耗，吊重将做等幅振荡。如果考虑吊重的升降运动，在这个过程中绳的拉力是要做功的，这就引起了系统能量的变化，可以使吊重做等幅、减幅或增幅运动。

图2 吊重摆振仿真模型

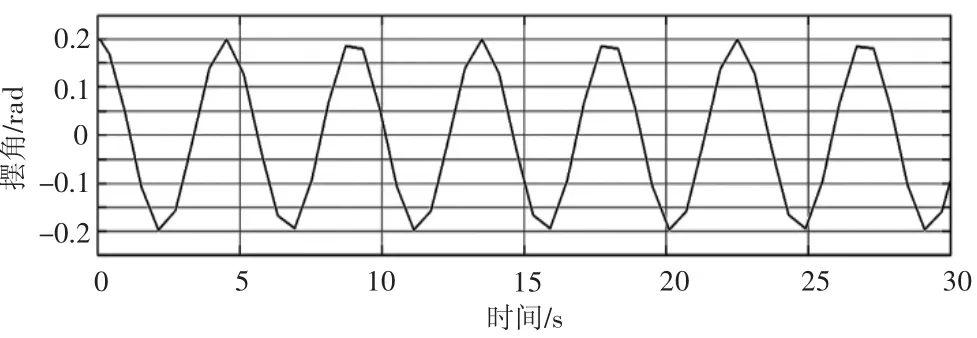
图3 吊重摆振曲线（a=0）

图4 吊重摆振曲线（a=2）

图5 吊重摆振曲线（a=-5）

对式（7）我们利用MATLAB中的Plot 函数绘制摆角曲线。设初始摆长L0=5 m，g=9.81 m/s2，A0=20°=0.35 rad，初始相位φ0=-π/2，γ=0.02，摆角曲线如图6所示。

图6 吊重摆角与时间的关系

从图6可以看出，采取与荡秋千相反的动作方式，即在最大摆角处提升吊重和平衡位置处下放吊重可以实现吊重的消摆。

4 结 论

本文针对井下起吊重物的摆动问题，采用与荡秋千模型相反的逆向思维过程，运用慢变振幅和相位法求得了吊重摆动的一次近似解，采用作图法绘制摆角曲线，可以直观地看出吊重的升降运动对吊重摆动的影响，即在最大摆角处提升吊重和在平衡位置处下放吊重能够实现吊重的减摆，在实际操作中，操作者可以通过简单的提升和下放来实现重物的消摆。此外，起重机小车加速度将使吊重摆幅增大，但它改变的是吊重的动态平衡位置。