一种非对称3－(2SPS)并联机构可达工作空间分析

王少锋，李开明

(南京理工大学机械工程学院，江苏南京210094)

0 引言

并联机构由于具有刚度大、承载力强、位置精度高、惯量小、响应快等优良特性，在工业生产、医疗卫生以及航空航天等领域均有广泛的应用［1］。目前，大多数并联机构均采用对称式结构设计，相对于非对称式并联机构，它具有正向求解容易，控制简单方便，加工制造容易等特性［2-5］。

然而，针对某些方向性能要求较高而其他方向要求相对较低的特殊应用场合，对称式的并联机构就不太合适［6-7］。例如，用于测试气体冲击射流的试验平台，被试验件的受力主要源自于气体射流的冲击力，其方向大体沿射流的冲击方向，因而在这一方向需要机构具有较好的稳定性;同时，为了能够动态模拟射流的冲击力，试验平台在射流方向还需要有较长的工作空间。据此特性，本文研究了一种非对称式3-(2SPS)并联机构，其动平台为等腰梯形，定平台上的6个铰链点成非对称分布，且不共面，其可达工作空间成逗号“，”型，可初步满足该实验要求。

1 机构描述

非对称3－(2SPS)并联机构的CAD模型图和结构简图如图1所示，它由定平台、动平台及连接两平台的6根可伸缩驱动支链组成。每根驱动支链均采用伺服电动机—滚珠丝杠副驱动，两端分别通过球铰与定平台和动平台相连。相邻的两根驱动支链采用伺服电动机同步驱动，组成一组平行双联驱动副，以约束动平台的转动，使其只有3个平移自由度。因此非对称3－(2SPS)并联机构为3平移并联机构，由并联机构自由度公式［1］：

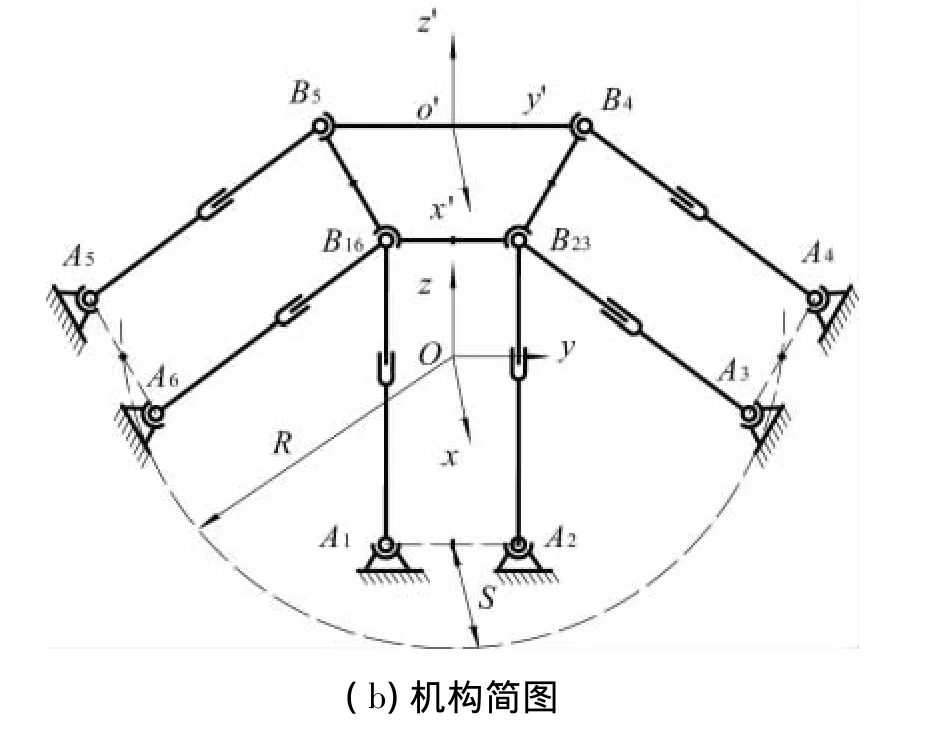
图1 非对称三自由度并联机构

式中：M表示机构的自由度;d表示机构的阶数;n为包括机架在内的构件数目;g为运动副的数目;fi表示第i个运动副的自由度;v为冗余约束数目;ε为机构中存在的局部自由度。

可知机构具有6自由度。但是，由于机构中包含3条同步驱动的运动约束，因此，具有平行双联驱动副的非对称3－(2SPS)并联机构的自由度为3。

机构动平台上的4个球铰成等腰梯形布置，梯形的平行短边长与腰长相等，即B5B16=B16B23=B23B4，其中平行短边B16B23的两端为复合球铰。最外侧的两组平行驱动副在定平台上的4个铰链点共面，且与中间杆组铰链的中点相距s，如图1(b)所示。

2 位置分析

如图 1(b)所示，建立动坐标系o＇－x＇y＇z＇和定坐标系o－xyz。定、动平台上各铰链点在坐标系中的投影几何关系如图 2 所示，图中点Ci，Ci＇(i=1，2，3)分别为每组平行驱动副的铰链点在定平台和动平台上的中点。动坐标系原点o＇为动平台的外接圆圆心，o＇x＇轴垂直于动平台;定坐标系原点o为C2C3中点，ox轴垂直于A3A4、A5A6构成的平面。∠C2C1C3=90°，C2C3=2OC1=2R，每组平行驱动副铰链点之间的距离相等且为h，动平台外接圆半径为r，梯形的底角为α，且有α=2arcsin(h/2r)。

根据几何关系，定平台中各铰链点在定系中的位置矢量为：

式中，p=h/2cosα，q=h/2sinα

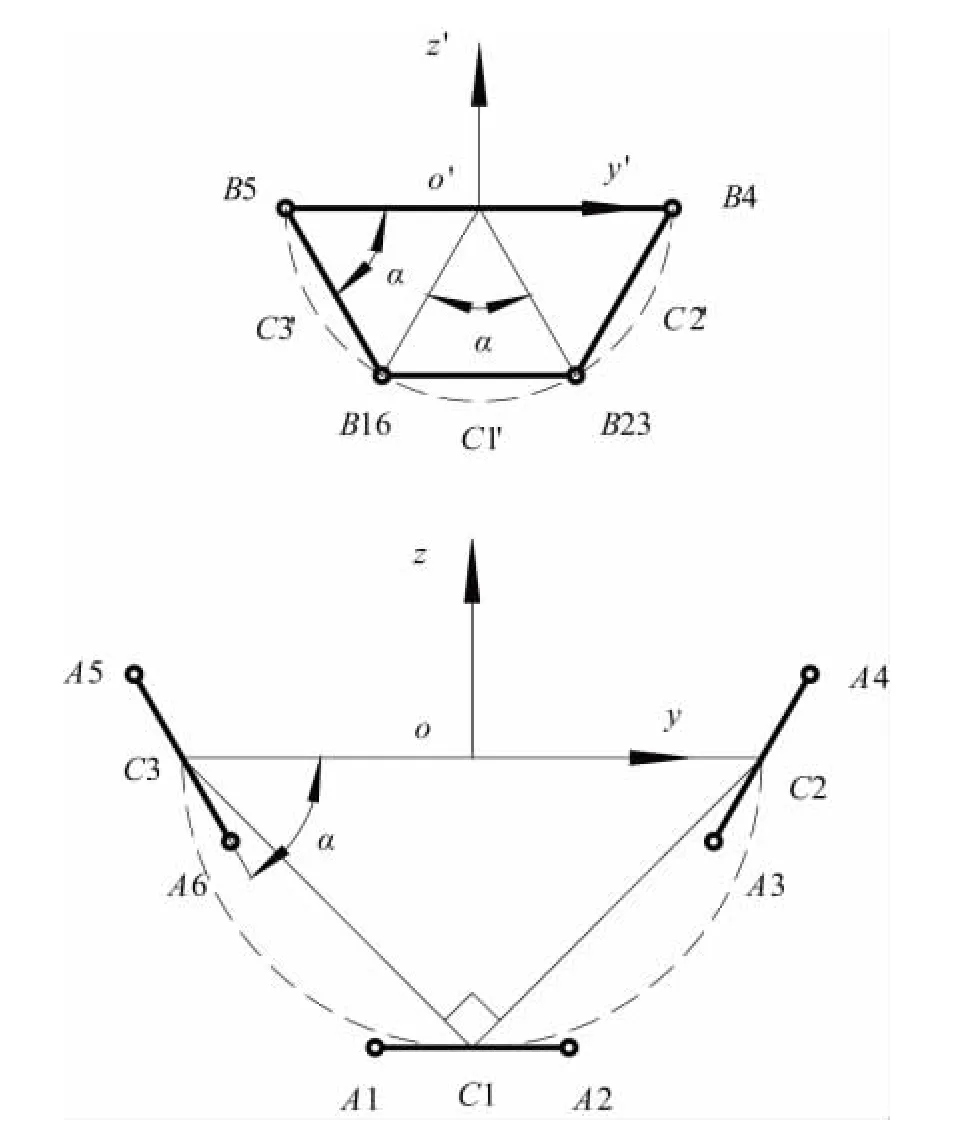
图2 定、动平台铰链点几何关系

同理，动平台各铰链点在动系下的位置矢量为：

式中，w=rcosα/2

由于非对称3－(2SPS)并联机构只具有3个移动自由度，因此其姿态变换矩阵为3阶单位矩阵I3。设动坐标系o＇－x＇y＇z＇在定系o－xyz中的位置矢P0=(x0y0z0)T，则动平台铰链点在定系中的位置矢量表示为：

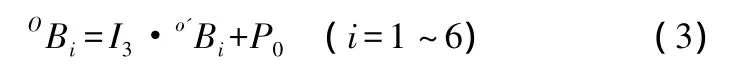
各驱动支链的杆长矢量在定坐标系中可表示为：

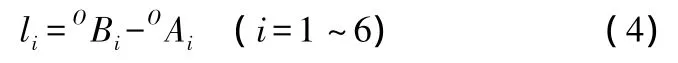
从而驱动杆的长度，也就是机构的反解为：

将上述各式代入式(5)中，即可得到非对称3－(2SPS)并联机构的唯一反解方程：

式中，t=R－w，m=R－p－h/2，n=q－w。

对(6)进行代数运算，即可得到非对称3－(2SPS)并联机构的位置正解。然而，由于并联机构结构的复杂性，位置正解的难度一般较大，在求解时通常采用数学推导软件来辅助求解。

对于式(6)，可以很容易的求解出y0：

将其代入式(6)后，式(6)可化简成一个二元二次方程组。借助于Matlab数值分析软件求解简化后的方程组，可以得到该机构的全部正解方程。从求解结果来看：y0，z0均为唯一解，只有x0具有两个解。这表明，非对称3－(2SPS)并联机构对应一组给定的驱动杆杆长，可能会有2种可能的位形，而这2种可能位形只在x轴方向的取值不一。

3 可达工作空间分析

并联机构的可达工作空间是指机构末端操作器上某一参考点可以达到的所有点的集合，它的大小是衡量并联机构性能的重要指标，也是进行机构设计的重要依据。影响并联机构工作空间的主要因素包括机构的结构尺寸、铰链的转角范围以及各支链之间的干涉等。其求解在很大程度上依赖于机构位置解的研究结果，至今也没有非常完善的方法。对于比较简单的机构，如平面机构，其工作空间的边界可以用解析表达;而对于空间6/6型并联机构，目前还只有数值法。

3.1 约束条件分析

影响非对称式3－(2SPS)并联机构可达工作空间的因素包括：驱动支链的长度限制，定、动平台上的球铰转角范围限制，以及每组平行驱动杆之间的支链干涉。

1)驱动支链长度限制。对于每根驱动杆，必须满足：

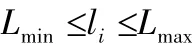
此处Lmin和Lmax是支链所能达到的最短长度与最长长度。当其中的一条支链达到最长或最短杆长时，上平台即处于工作空间的边界位置。

2)球铰转角范围限制。球铰副的转角由球铰的姿态向量npi和与球铰相连接的驱动杆的方向矢量li来确定。设球铰的许用半锥角为θmax，则驱动杆的转角θ需满足：

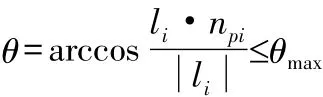
3)平行驱动杆之间的支链干涉。假设Di(i=1～3)为每组平行驱动杆中心线之间的最短距离，由于每一组平行驱动杆在运动的过程中始终保持平行，则它们不发生干涉的条件为：

式中：D为驱动杆的最大直径。

3.2 实例计算分析

设定该机构的动平台外接圆半径r=350mm，平行杆铰链点间距h=350mm，α=60°;定平台外接圆半径R=620mm，s=300mm;伸缩杆最短lmin=650mm，最长lmax=1200mm，杆最大直径D=80mm;球铰的转角范围 θ=70°。

借助Matlab数值计算软件，采用边界搜索法绘制出非对称3－(2SPS)并联机构可达工作空间的三维表面图，如图3所示。图4为工作空间在二维平面上的截面图。

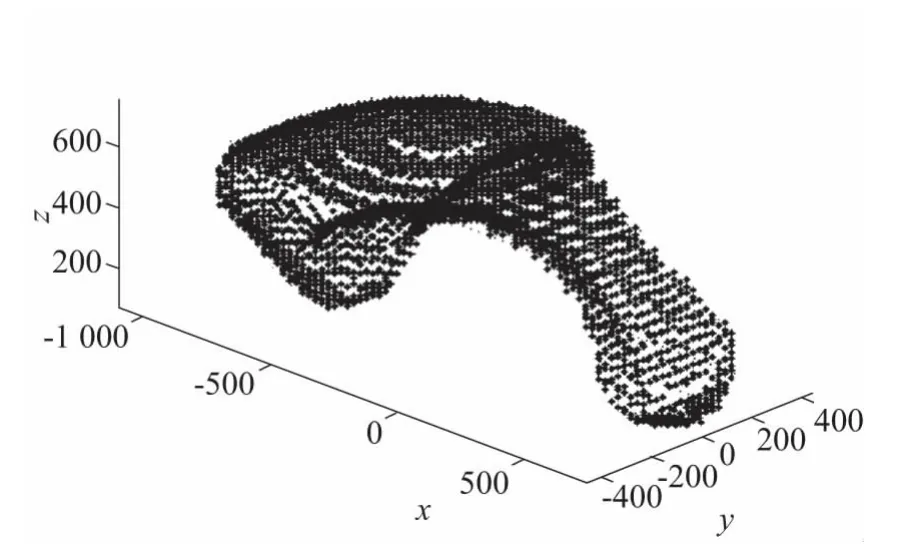
图3 工作空间三维表面图

图4 工作空间二维截面图

从图3中的整体外形来看，非对称3－(2SPS)并联机构的可达工作空间形似逗号(“，”)，其左侧较大，右侧狭小，中间向上拱起，边界表面为光滑的弧形，内部不存在空洞。从图4(a)、图4(c)可以看出，该机构的工作空间关于xoz平面对称。从图4(b)可以看出，机构在左半部分有较大的工作空间，而这一侧也正好是中间杆组偏置的那一侧;在右半部分则为一条狭长的弧形。

利用左侧区域，可以定姿态测量冲击射流，并且具有较大的调节范围;而左侧至右侧的这一狭长区域，则可用来动态模拟冲击射流。

4 结论

在对非对称3－(2SPS)并联机构进行位置分析的基础上，借助于MATLAB软件绘制出了该机构的可达工作空间三维表面图及在各坐标轴方向的二维截面图。从分析的结果可以看出，非对称3－(2SPS)并联机构的可达工作空间可基本满足气体冲击射流对测试平台结构的要求，为后续研究提供了参考。

［1］黄真，赵永生，赵铁石.高等空间机构学［M］.北京：高等教育出版社，2006.

［2］王银，李开明.并联机器人单支链伺服控制研究［J］.机械制造与自动化，2011，40(6)：167-170.

［3］高继良，李开明，陈有清.3－(2SPS)并联机构的工作空间分析及结构参数对其影响分析［J］.机床与液压，2011，39(23)：51-54.

［4］陈海真，邹忠月，郝秀清.一种新型三平移并联机构运动输出及工作空间分析［J］.机床与液压，2010，38(5)：24-26.

［5］姚裕，吴洪涛，张召明，等.基于并联机构的六分量并联天平及其力雅克比矩阵研究［J］.机械科学与技术，2004，23(7)：768-770.

［6］吴孟丽，张大卫，赵兴玉.一种新型非对称并联机构的运动学分析［J］.中国机械工程，2008，19(12)：1423-1428.

［7］胡波，路懿，许佳音.一种新型两移一转非对称并联机构的运动学及静力学［J］.燕山大学学报，2008，32(4)：290-294.