基于灰色关联理论与多元线性回归模型的铁路客运量预测

杜先汉，李 岩

（1.武汉市政工程设计研究院有限责任公司，湖北 武汉 430023；2.西南交通大学 交通运输与物流学院，四川 成都 610031）

铁路客运量是反映铁路客运发展水平的最重要指标之一，对铁路的客运量进行有效地预测有助于相关部门在客运市场的竞争中制定合理有效的策略。随着我国经济的持续高速发展和人民生活水平的不断提高，人们的出行需求不断增大，同时，我国客运市场竞争愈加激烈，公路、民航业的分担率逐年增加，面对激烈的市场竞争，对影响铁路客运量的因素作系统分析，对客运量进行预测显得尤为重要。

1 客运市场因素的定性分析

铁路旅客运输是使用铁路客运列车将旅客从一个地方运送到另一个地方的过程。它作为一个系统，是由许多共同影响、关联和作用的子系统构成。

仅从铁路客运系统自身的角度出发，分析客运量内部影响因素：

1）营业里程，是反映铁路设备数量的首要指标。客运量随着营运里程的增加而增长，但不呈现一般的数学关系。

2）列车旅行速度，指列车在区段内运行的平均速度。列车运行车速越高，旅客乘车需要的时间越短，越能吸引更多的旅客。

3）客车保有量，反映现有客车数量。客车保有量是铁路旅客系统运能的重要指标，直接约束铁路旅客系统的运量。

铁路客运系统作为交通运输系统的一个子系统，客运量受外部因素的影响。

1）国民经济发展水平。改革开放以来，我国的社会经济一直保持着高速发展，2010年国民生产总值GNP 达到了183 618.5 亿元，增长率一直高于10%。社会经济的快速增长，使得人们出行次数增加。

2）人口发展及其结构。我国是一个人口大国，2010年全国人口数是134 091万人，全国平均每人每年乘火车出行的次数为1.25次。“十二五”纲要指出，到2015年人口控制在13.9亿左右，按平均每人每年乘火车出行1次计算，到2015年客运量将增长0.6亿人。从人口的结构上看，城镇人口将首次超过农村人口，城镇居民的出行需求要大于农村居民，影响客运量的增长。

3）国民收入与消费结构。近年来，随着国民经济的高速增长，人民生活水平得到显著提高。据统计，我国2010年的国民收入为341 401亿元，人均国民收入为30 074元是2006年的1.9倍，消费水平则增加了45.3%。居民收入增长和消费水平增高，同时，居民用于交通方面的消费也会有显著提高。

从铁路客运系统的内部和外部环境，分析影响客运量的大小主要因素，但还存在着许多其他不确定的因素影响着铁路客运量的大小。

2 灰色关联理论在客运市场因素分析

灰色系统是指系统中的信息部分已知，部分未知的系统。对于部分信息不确定的系统，十分适合运用灰色理论进行分析。

灰色关联度理论是根据因素之间发展态势的相似或相异程度，衡量因素间关联程度的方法。关联度的分析，是按照对象的发展趋势作出的分析，不需要以典型的分布规律为基础，对事物的样本量也没有要求，计算量较小，且不会出现关联度的量化结果与定性分析不一致的情况。关联度分析方法原理如下

设有m个与母因素（X0）有一定关联作用的子因素（X1，X2，…，Xm），它们都至少有N个逐年原始数列，其值简称序列。

母序列：｛x0（k）｝，k＝1，2，…，N；

子序列：｛xi（k）｝，i＝1，2，…，m；k＝1，2，…，N。

方便比较，进行标准化处理：

令

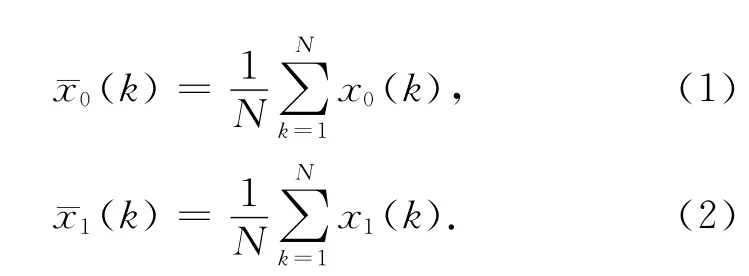
标准化

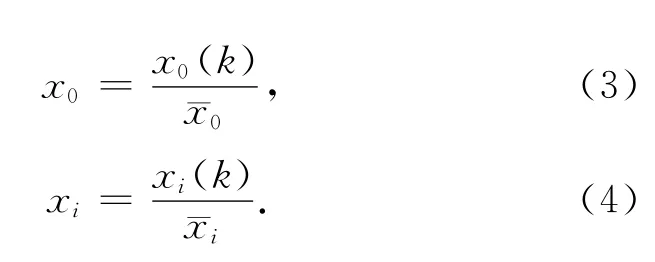
于是tox坐标系有折线：X0（k），X1（k），…，Xi（k），…，在t轴上有一定的长度，假设这些折现有交点（参考点），则第i条子线在k时刻与母线在同时刻的距离Δ0i（k）＝X0（k）－Xi（k），显然，Δ0i（k）愈小，子线与母线在k时刻的关联性愈好。

关联系数计算：

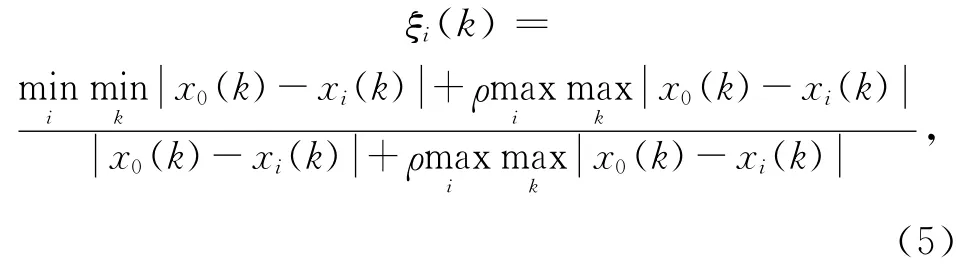
式中：ξi（k）是第i条子线与母线X0在k时刻的关联系数，其值满足0≤ξi（k）≤1，ξi（k）愈接近1，它们的关联性愈好；ρ是分辨系数，一般在0～1取值，本文取ρ＝0.5。

关联度

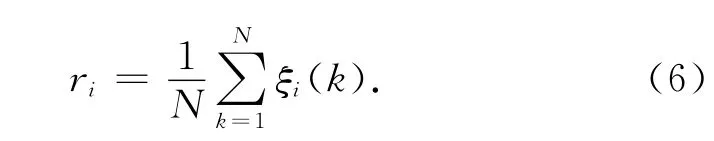
ri就是衡量系统因素之间关联性的一个量度。显然因素自身的关联度ri＝1，据经验，在ρ＝0.5 时，ri≥0.6即认为子因素与母因素有关联。

如rj＞ri，则认为Xj对X0的关联度大于Xi。

3 多元线性回归模型简介

3.1 基本原理

根据灰色关联度大小选取的m个预测因素与预测对象进行线性拟合，建立多元线性回归方程：

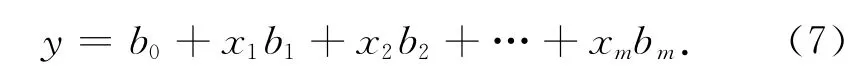
式中：b0，b1，b2，…，bm为回归系数；x1，x2，…，xm为预测因子。

回归系数可根据数据资料按最小二乘法确定。对上式应用最小二乘法可导出方程组：

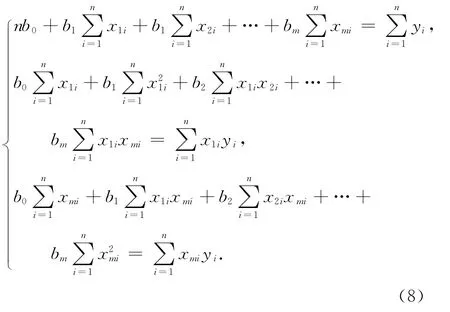
式中：xik为第i个预测因素的第k年的数值（i＝1，2，…，m；k＝1，2，…，n）；yi为预测对象的第k年观测值，i＝1，2，…，n；n为年数；m为预测因素总个数。

3.2 回归效果检验

求得回归方程，需要对其回归效果进行检验。由于y值是一个随机变量，对于每个y的观测值来说，该次观测值与其均值y的离差即使观测值大小，其n次观测值的总变差为

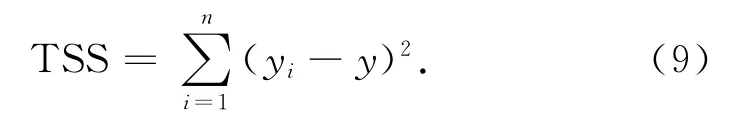
观测值与估计值之差的平方和称为残差平方和为

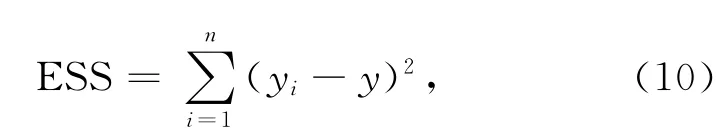
估计值与均值y之差的平方和，称为回归平方和为

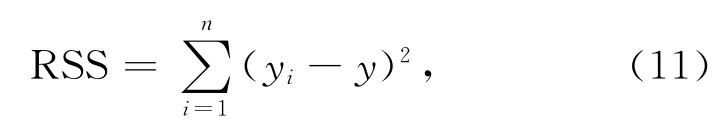
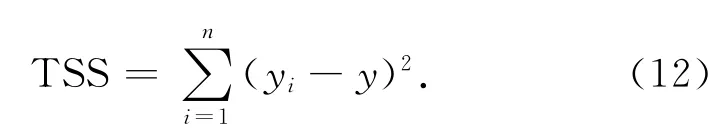
检验y与预测变量x1，x2，…，xi之间的线性关系是否显著，构造统计量为

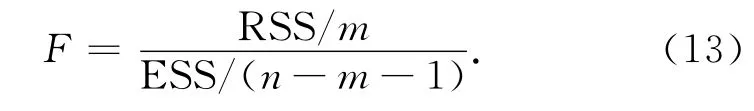
查表得到Fa（m，n－m－1）的值，若F＞Fa，拒绝原假设，回归方程显著，反之，回归方程不显著。

4 应用实例

根据我国2004—2010年的铁路客运情况，采用灰色关联度的分析方法对铁路客运量及其影响因素进行分析。

4.1 铁路客运量影响因素的关联度计算

以铁路客运量逐年原始数列为母数列X0；

以全国总人口、营业里程、国民生产总值、旅客列车旅行速度等有关因素的逐年（2004—2010 年）原始数据列Xi为子数列（见表1）。

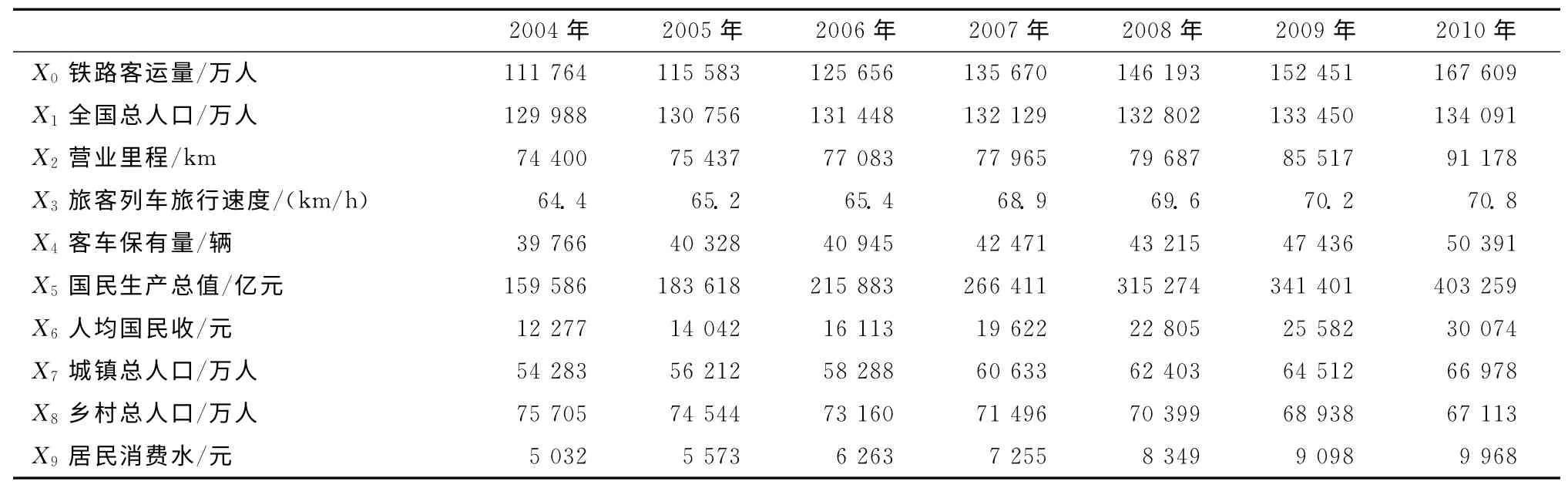
表1 铁路客运量与预测因素数据

按式（1）、式（2）、式（3）、式（4）标准化后见表2。

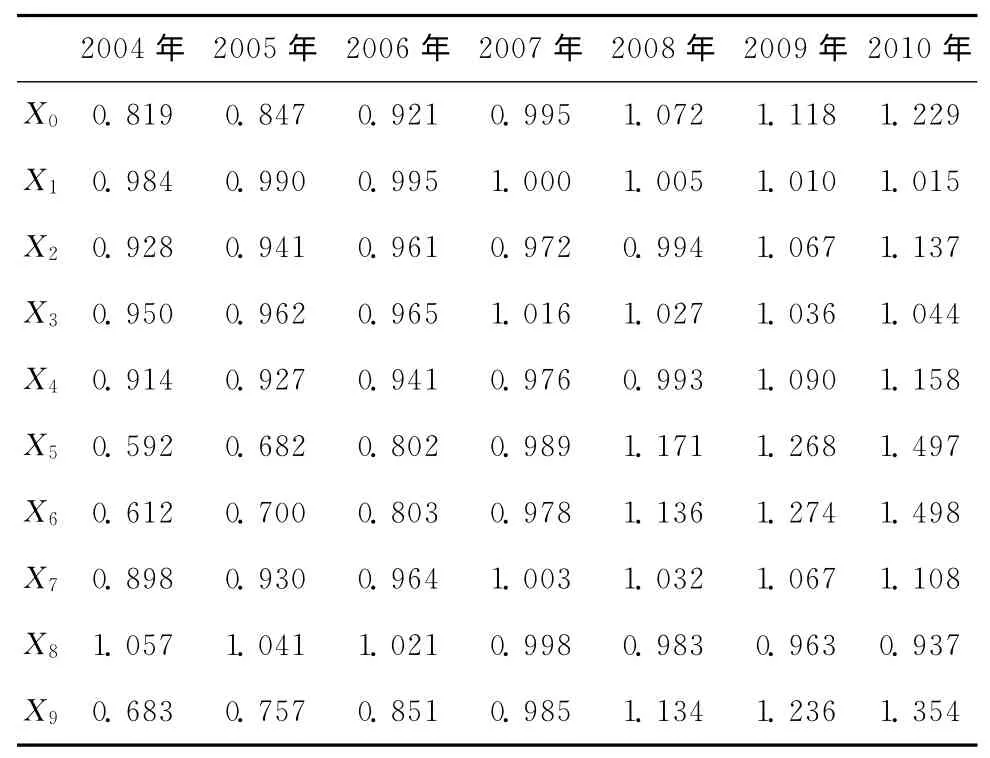
表2 初值化数据

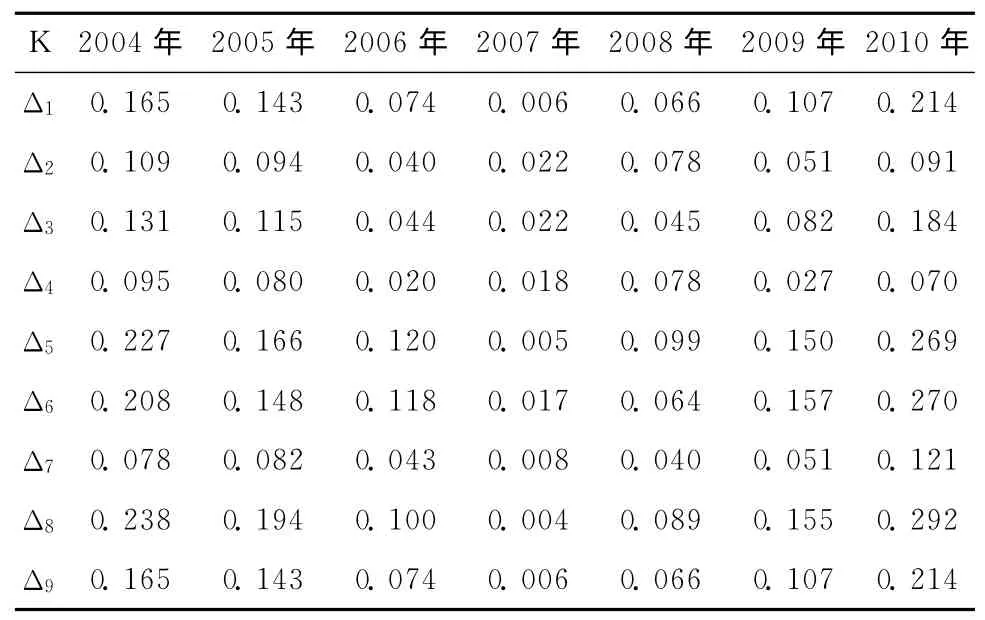
表3 相应数列绝对差

由式（5）见表4。

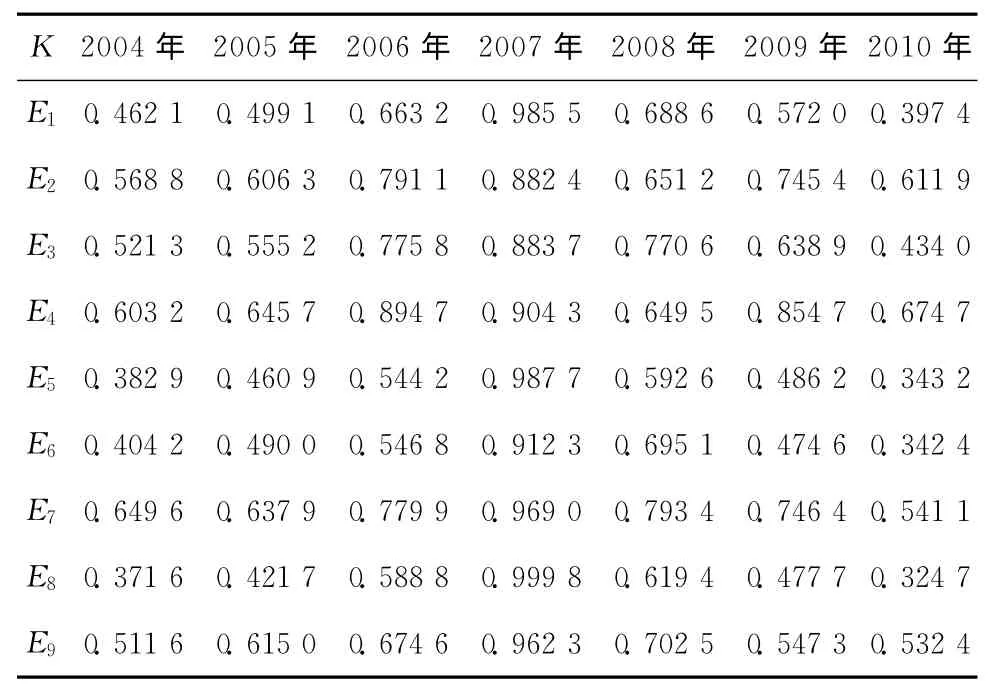
表4 关联系数

由式（6）得

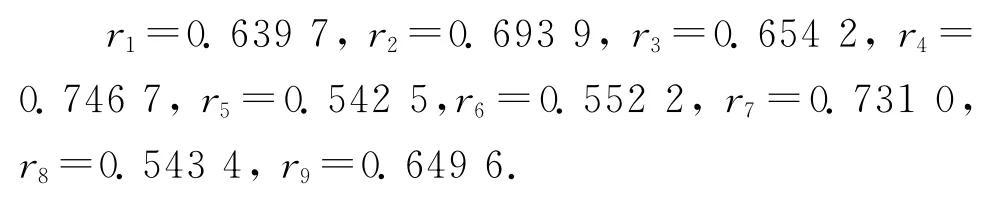
由大到小降序排列为

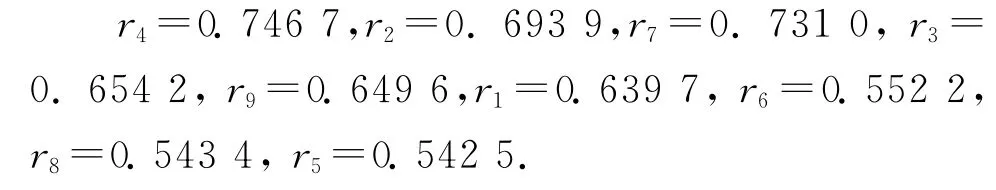
即影响客运量的因素主次关系如下：客车保有量＞营业里程＞城镇总人口＞旅客列车旅行速度＞居民消费水平＞全国总人口＞人均国民收入＞乡村总人口＞国民生产总值，如表5所示。

表5 客运量与各因素的关联度及排序

4.2 回归拟合

按照前述的关联度计算，取与客运量关联度较大的3个要素进行回归分析.设客运量为参考序列y，城镇人口、营业里程、客车保有量分别为x1，x2，x3，将已知实测数据代入根据最小二乘法建立的正规方程组（8），得回归方程为

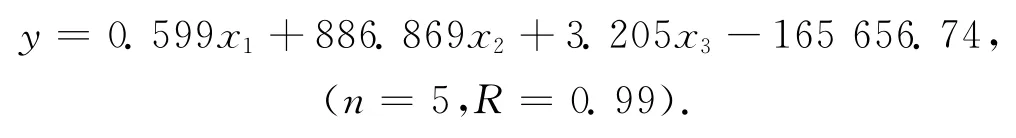
4.3 回归效果检验

应用式（10）计算观测值与估值之间残差平方和：

EES＝19 209 609.06.

应用式（11）估值与均值y之间回归平方和：

RSS＝2 464 573 675.

应用式（13）计算F检验统计量：

F＝128.299.

选择显著水平α＝0.01，根据Fα（3，3）查F分布显著性检验值Fα＝29.456，F＞Fα。因此，在α＝0.01的水平下，回归效果是显著的。

4.4 成果检验与评价

应用所建预测模型对2004—2010年的铁路客运量实际系列进行比较，见表6。

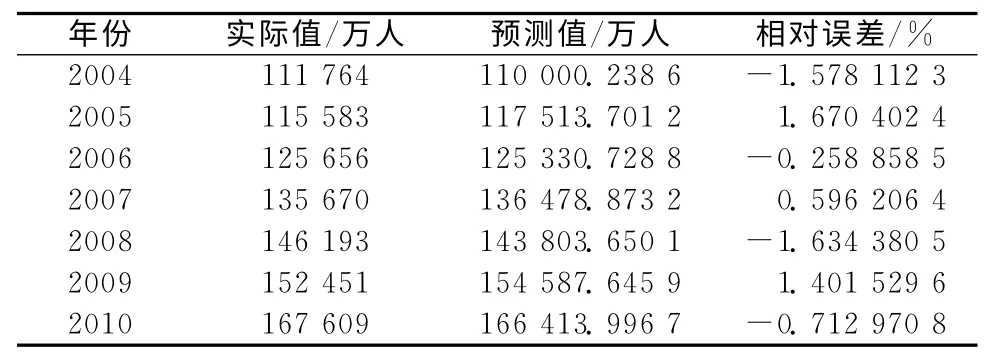
表6 客运量拟合分析

从表6 可以看出误差在±2%以内，预测精度较高。

5 结束语

铁路客运系统的信息相对匮乏，统计数据的灰度较大，运用灰色关联分析可以在样本量较少的情况下挖掘出影响铁路系统客运量改变的主要因素，减少了变量分析计算的工作时间。利用基于灰色关联分析的多元回归模型对铁路系统的客运量进行预测，可以充分利用影响铁路系统客运量改变的主要因素。本例证明，模型具有较高的预测精度，是一种较为简单且有效的预测方法。

［1］刘敬青，叶效鹏，张国伍.灰色关联理论在铁路客运市场分析的应用［J］.系统工程理论与实践，1998，3（3）：26－28.

［2］邓聚龙.灰色系统［M］.北京：国防工业出版社，1985.

［3］张国伍.交通运输系统分析［M］.成都：西南交大出版社，1991.

［4］魏光辉，董新光，杨鹏年，等.基于灰色关联分析与多元线性回归模型的水面蒸发预测［J］.节水灌溉，2010，2（41）：26－30.

［5］殷英，陈森发.基于数据预处理的铁路客运量灰色预测模型［J］.交通科技与经济，2007，9（6）：52－54.