交通枢纽车道边动态容量分析

张艳聪

（同济大学 建筑设计研究院（集团）有限公司，上海 200092）

1 单车道车道边容量模型

对于最简单的落客区在车道边布置一个停车道和一个通过性车道，Parizi和Braaksma设计了一个模型，并根据模型计算出了车道边一定时间内能处理的最大动态容量。

所谓动态容量是指一定的交通条件下，在保证旅客车辆连续到达的情况下，单位时间内车道边系统处理的最大车流量。动态容量是车道边的一种性能，是度量车道边疏导车辆和旅客能力的指标，确定车道边容量是交通枢纽规划设计中需要。

Parizi的模型中没有考虑建筑进出入口的位置和数量，也没有考虑值机柜台的位置等因素，应用于两车道的车道边组织形式，是一个反映理想状态下最大动态容量的模型。停车模型如图1所示。

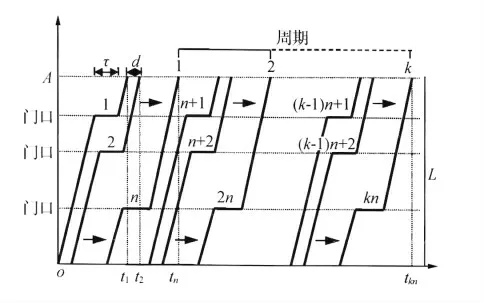
图1 单车道车辆容量模型

其中τ为车辆停车后上落客直至离开停车位之间的时间间隔，d为车辆之间的影响时间，也是延误时间，d＝α／v，α为车辆平均影响长度，车道边总长度为L。

模型中认为所有停车位的使用率相同，这样才能得到最大交通饱和容量，即所有车辆可以选择车道边系统中任何一个停车位进行停车。那么车辆的停车时间分别为

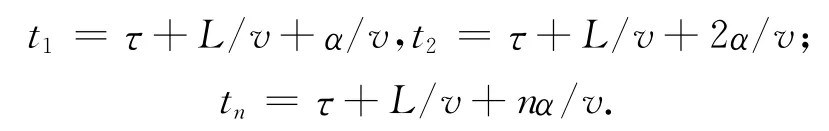
第2个周期

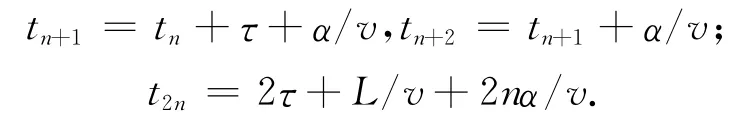
第k个周期

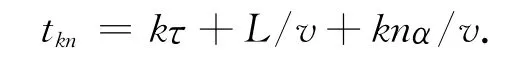
用时间T代替tkn

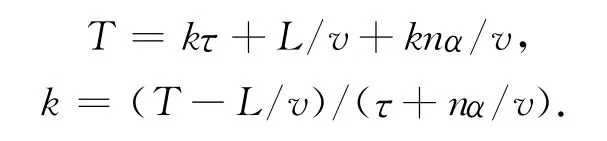
假设有n个停车位，则T时间内最大理想动态容量为

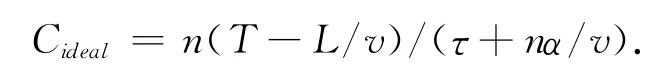
考虑实际中会有不规范停车、驾驶员喜好以及便利性等因素的影响，停车位的使用率是不同的。提出有效停车位数的概念，则实际动态容量为

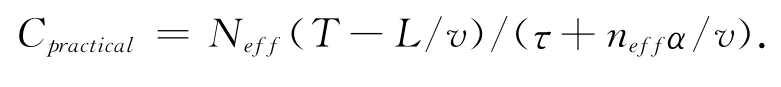
2 双车道车道边容量模型（两个停车车道一个通过性车道）

由于实际情况要比理想情况复杂的多，而且有诸多设计形式的不同，大多数车道边停车道都大于一根，因此，根据以上单车道车道边模型，进行双车道车道边动态容量分析（见图2）。双车道车道边模型中有两根车道用于停车，其动态容量绝不是简单的单车道的两倍，现将两根车道分为内外两根进行考虑。外侧车道同单车道原理相同，内侧车道车辆停靠较复杂。对于内侧车道，假定到达内侧车道的车辆中有n～θ辆完成停靠后自内侧车道离开，其余θ辆需要穿越外侧车道进入通过性车道然后离开，假定这部分车辆穿越外侧车道时要等待的时间为ta。

则内侧车道车辆离开时间分别为

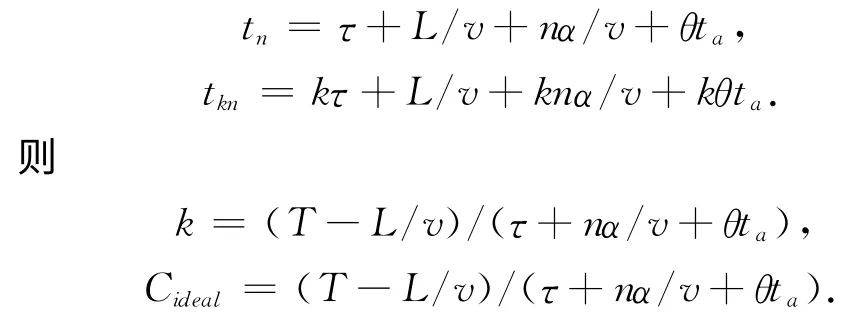
内外侧车道边停车位有效率不同，分别设为Neff1和Neff2，双车道车道边动态容量为内外侧容量之和

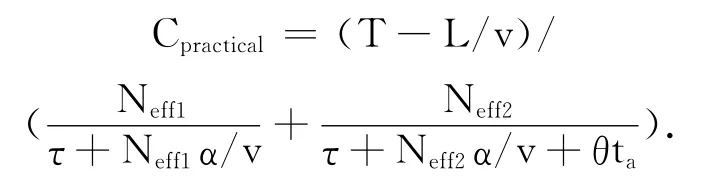
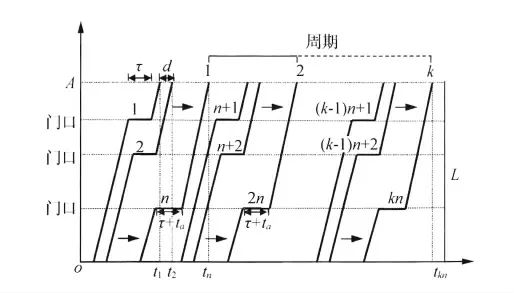
图2 双车道内侧车道边动态容量模型

3 车辆间平均影响时间

一般地，较大型交通枢纽通常采用进站客流和出站客流分离的方式，相应的车道边也分为出发车道边和到达车道边，对于到达车道边私人小汽车一般不允许进入接客，出租车、大客车等也是按照交通管制，乘客也是排队上车，交通比较有秩序，因此，以下研究均以出发车道边为主进行分析。车辆间影响时间由两部分组成，一个是车辆进入停车位之前受前方车辆影响的时间。另一个是车辆离开停车位时汇入车流的时间。

3.1 前方车辆影响时间

车辆进入停车位对后续车辆的影响时间：不考虑车辆未完成上落客，后续车辆等候进入相同停车位的情况。

3.1.1 不超车

第一辆车停车位置靠前，后续一辆车预期停靠的位置在第一辆车后边，这种情况下基本不受前一辆车的影响，可以认为车辆影响时间为0，因此，不予考虑。

3.1.2 超车

第一辆车减速进入停车位，后续车辆不得不因该辆车的停靠而减速甚至停车，用下图描述交通波的形成与传播轨迹。设第二辆车减速时刻为零时刻，对应位置为零位置，即坐标原点O 是第二辆车的变速点，当第二辆车因为第一辆车的停靠而减速时，接着第三辆车也减速，其开始减速的位置更靠后。直线OB显示了停车波的动态轨迹，它的斜率就是停车波的波速。直到第一辆车完全停进停车位或不影响后续车辆前进时停车波开始消散，如图中A 点。其中ts为第一辆车停入停车位所用时间。根据车流波动理论，设停车波波速为v1，减速波波速为v2，因降速而耽误的平均时间为0.5（ts－tr），因此

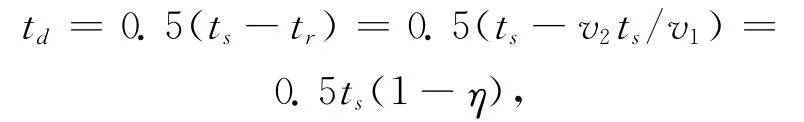
其中η＝v2／v1.

根据车流波动理论，车辆影响长度受第一辆车进入停车位的所用的时间影响最大，尤其是在第一辆车的停靠位置靠前的情况下，后续车辆都会受到影响，而且它停靠的时间越长，停车波越长，车辆影响时间也就越大（见图3）。

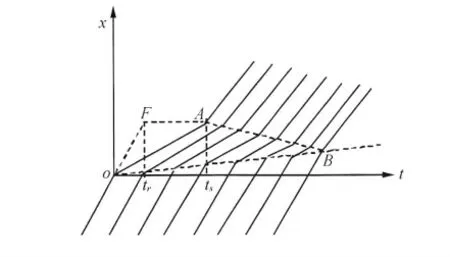
图3 车道边车辆停靠时间空间运行波动

3.2 汇入时间

车辆完成落客后离开停车位，假设前方停车位还有车辆停车，则该车选择汇入外侧车道尽快离开。在进入外侧车道时类似于支路车流汇入主路车流。当外侧车流车流间隙大于可接受间隙时车辆就可以汇入，否则还需等待，这个间隙成为可接受间隙。假定外侧车流的到达服从泊松分布，到达率为λ辆／s，可接受间隙t，则车头时距大于t的概率为

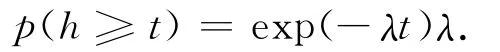
车道边有一辆车将汇入外侧车道，其汇入的概率为exp（－λt），有两辆即将汇入，其概率为［1－exp（－λt）］exp（－λt），则n辆车平均等待时间为

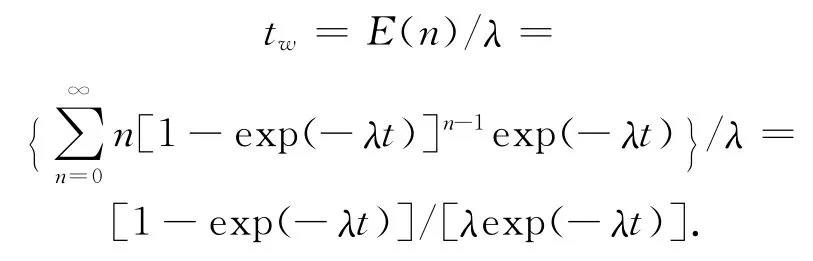
可见，汇入时间受可接受间隙和到达率的影响。

4 平均服务时间

影响动态容量的一个重要因素是车辆的停车时间，停车时间是随机的，经过对上海市虹桥机场和杭州市萧山机场车道边的小型车（包括出租车和私人小汽车）进行调查，获取180个有效数据并进行分析，得出停车时间分布并检验分布类型。将数据按5s为区间进行划分，如表1所示。

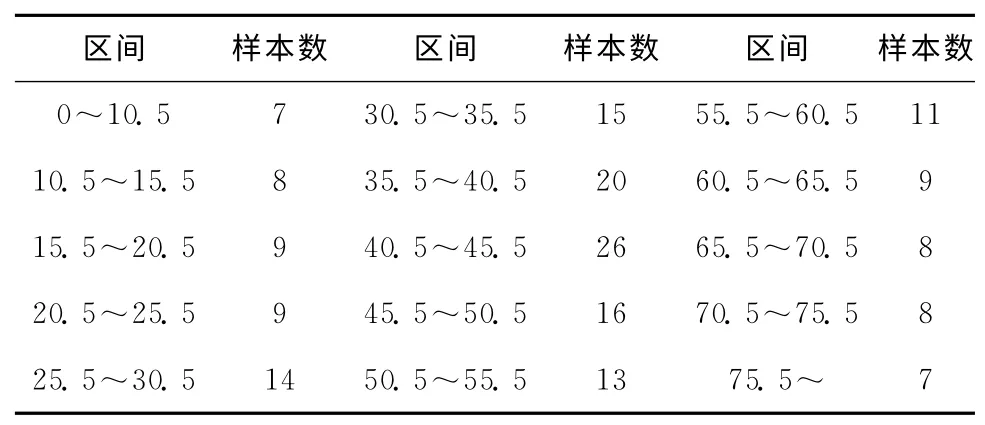
表1 车道边停车时间数据统计

经过分析，平均落客时间（见图4）为43.12s，均差为20.25。通过计算在显著水平0.05条件下，得到χ2检验统计量的观测值χ2＝9.451，临界值（12）＝21.028，可见9.451＜21.028，因此，可以认为停车时间基本服从正态分布N（43.12，20.252）。

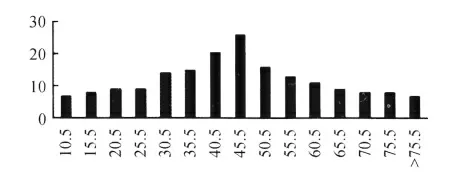
图4 落客时间分布直方图

5 分 析

根据以上分析，双车道动态容量计算公式为

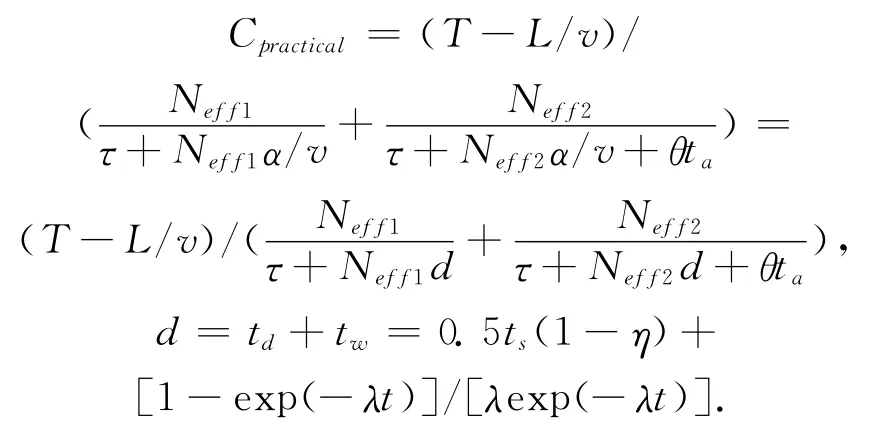
通过模型分析发现影响动态容量的因素除了有效停车位数以外，还有3个时间因素：停车时间、前方车辆影响时间和汇入时间。不同枢纽、不同地域、不同管理方式有效停车位数不同，有效停车位的问题很复杂，影响因素也很多，在此暂不做讨论。然而，停车时间是一个不可控的随机参数，根据调查结果的分析，在实际设计和研究中该参数可采用正态分布。前方车辆影响时间和汇入时间是两个影响容量的关键因素，因此，要想从设计上提高动态容量，只能减小前方车辆影响时间td和汇入时间tw。

为了达到减少前方车辆影响时间和汇入时间两个因素的目的，考虑将一般的平行式停车布置形式改为斜停式（30°、45°或60°），如图5、图6所示。

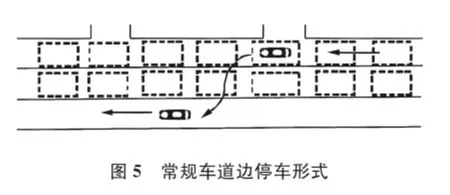
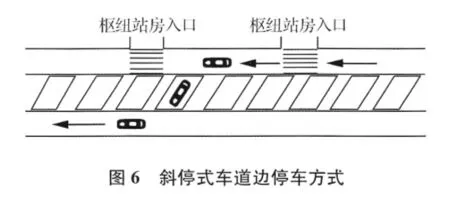
斜停式布置形式，克服了不同车辆类型之间交织的缺点。而且根据机动车机械性能，很明显斜停式要比平行式易于停车，因此，车辆进入停车位时ts明显减小，前方车辆间影响时间减小；同时，采用斜停式车辆离开停车位汇入车流时的可接受间隙t减小，汇入时间减少。所以，这种布置方式可以提高车道边动态容量，有关部门设计可以借鉴这种布置方法，使车辆在车道边的停靠更有序。

6 结束语

本文运用交通流理论，借鉴国内外相关成果，在单车道动态容量模型基础上提出了双车道车道边动态容量的计算方法，考虑了前方车辆影响时间以及汇入时间两个时间因素，建立了完整的双车道动态容量模型。并在调查数据的基础上得出车辆落客时间服从正态分布的结论。最后，根据得到的模型优化了车道边停车位布置形式，理论表明可以提高车道边动态容量。本文在分析中对交通流运行过程进行了一定的简化，与实际情况并不相符，有待于进一步研究。

［1］余朝玮，柳伍生，晏克非.虹桥综合客运枢纽车道边规模论证与仿真评价［J］.交通与运输，2007（7）：45－48.

［2］Mahmoud S.Parizi，John P.Braaksma.Optimum Design of Airport Enplaning Curbside Areas［J］.Journal of Transportation Engineering，1994，120（4）：536－551.

［3］Lester A.Hotel，Evaluation Inprovements In Landside Access For Airports［R］.Virginia Transportation Research Counci.

［4］Mumayiz S A.Evaluating performance and servicemeasures for the airport landside［C］.Transportation Research Record，1991，（1296）：25－31.

［5］Lemer A C.Measuring airport landside capacity［R］.Transportation Research Record，1988，（1199）：11－18.

［6］张兰芳，王知，方守恩.机场航站楼路边交通容量需求分析［J］.同济大学学报（自然科学版），2007，35（4）：486－490.

［7］李旭宏，唐怀海，吴炼，等.综合客运枢纽车道边通行能力分析［J］.公路交通科技，2009，26（4）：128－132.

［8］王秋平，古自鹏，袁伟，等.城市公交系统优化设计［J］.交通科技与经济，2012（5）：57－59.