梯度法优化下的机场跑道容量结构分析

马 昕，李 夏

（中国民用航空飞行学院 空中交通管理学院，四川 广汉 618307）

地处天府之国的成都双流国际机场，历经56年的蓬勃发展，如今已经成为中国第四大航空交通枢纽，其客运吞吐量于2012年突破3 000万人次，达到3 159.5万人次，并预计2015年突破4 300万人次，2020年突破6 300万人次。民航业作为新中国成立以来的朝阳产业强势发展，成都双流国际机场的客运、货运吞吐量也在迅猛增长，发展与增长背后也带来了对空中交通管理体系的严峻考验。以往有条不紊的实时管理手段依然重要，但对重点季节、重点时段的强化监管，以及对产业发展势头的前瞻性预测就显得尤为重要。成都双流国际机场，以每年平均10%以上的增长率快速增长，其各个时间段的跑道容量、航班起降次数都不会是平均分配的，利用梯度法找出选取指定时间段内的跑道容量结构组成，航班起降次数的极大值极小值，这些极值就可以认为是选取指定时间段内跑道容量结构利用率的构成，通过跑道容量结构分析对重点时间段强化监管，以及预测类似时间段的跑道容量，评估机场饱和度，从而达到应对日益增长的空中交通运输管理需求。

1 梯度法的基本概念

梯度法（又名最速下降法），指若存在函数F（a），在其取值范围内存在ai点，则F（a）在该点存在用一个梯度▽F（a），其为一向量，取正梯度和负梯度分别可求出最大值和最小值。通过定义初始点a0，从该设定点出发沿正梯度推导，则▽F（a）上升最快

C（0）＝▽F（a0）.

其中C（0）表示沿推导方向取值。

对于推导方向上的任意点aj在正梯度的向量表示为

C（j）＝▽F（aj）∕‖ ▽F（aj）‖.

当F（a）在正梯度上从0取道j，若再继续沿此方向推导向量长度Ej，则

aj＋1＝aj＋EjC（j）.

此时F（a）在取aj＋1时其值

F（aj＋1）＝F｛aj＋EjC（j）｝.

其关键在于推导向量长度E的选取，这一选取及其递增选取，可以在后面的程序中讨论，以及初始点的选取，依次类推所有的aj组成一个数列

a0，a1，a2，…，aj，aj＋1，…，ak.

该数列在一定条件下爬升，使得F（a）在ak时取得最大值。

2 梯度法优化下的跑道容量分析

梯度法的优化算法运用十分广泛，以往庞大繁杂的计算机程序得以极大简化，不仅使程序本身空间占有量得到控制，也让操作者的使用变得简捷，程序运算速度也得到加强。反观民航数据的发展与统计，除了日常统计、机场保障、公司收益等经济需要以外，作为各级地方政府对机场扩建、跑道增加，各级空管部门对空域容量的评估、工作人员的调配等问题都依靠日积月累的基础数据统计作为依据。面对这些数据，单纯的统计已经稍显繁重，而这些数据的时时快捷调用往往就让人力不从心。

2.1 跑道容量构成

对于不同的机场有着不同的管理思路，以成都双流机场为例。首先取一年中最为繁忙的春运期间某天数据，以15 min为一个结点（即0：0：0～0：14：59区间内15min内的起降架次之和）统计起飞架次，如图1所示，一天中机场起飞架次最为集中的时间段是7：00～8：00、21：30前后，可将当日航班起飞架次图形看似两个波峰的平滑曲线，则可直观反映出双流机场于当日这两个时段起飞最为繁忙。同取当日飞机降落架次数据，如图2所示，一天中机场降落架次最为集中的时间段是11：00前后、13：00前后、16：00前后、19：00前后及0：00前后，同样，看作一段平滑曲线，可直观反映出双流机场这5个时段降落最为繁忙。又因为起飞与降落为同一机场内的双跑道上交替进行，故将两段曲线叠加得出，当日双流机场6：00第一架升空后，从7：00前后开始，大约间隔3h左右即迎来一段波峰时刻，此时双流机场起降架次最为频繁，跑道容量的使用率达到最高，通过波峰、波谷的变化节奏，反映出机场跑道容量的变化趋势。不过即便如此，每15min为一结点以及单日统计量较小等特殊情况存在，使得需要找出一种既操作简便又快捷准确，且能对庞大数据进行运算的方式。

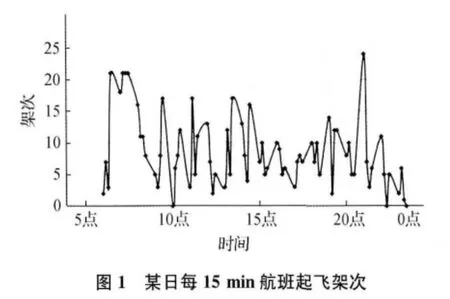
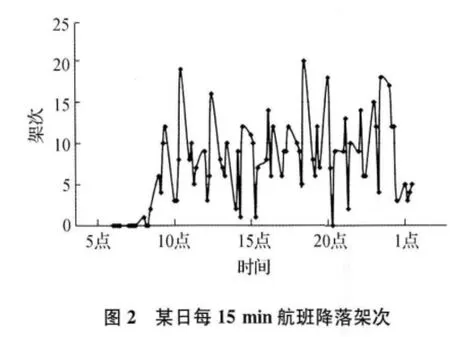
2.2 梯度法优化下的跑道容量结构分析

对于长时间的庞大数据处理，使用上面简单的统计方式就很难实现了。基于梯度法优化的应用日趋成熟和简便，把相邻两段时间的起降架次做比较，若一直存在

则表明▽F（a）依然存在正梯度上升空间。当且仅当

F（aj）–F（aj＋EjC（j））≤γ.

γ可设定为＞0的实数。

则表示▽F（a）不再具备正梯度上升的空间，转而向负梯度下降，如图3所示，初始化a0在实数范围内取值，调用数据库中指定时间段中任意时间点的跑道容量数据，设置允许的误差范围θ，γ，检验梯度向量并附值F（aj＋1），通过判断F（aj）–F（aj＋EjC（j））≤γ是否为真，为真则表示后面数据小于之前数据，则代表一个波峰的结束，为假则表明仍有上升空间，此次波峰尚未来到，需继续循环程序下去，最后得出结果。

图3 原函数f（x）

若统计整年甚至更长时间，在选定时间段内的双流机场跑道容量结构分析，就会显得更加复杂，不可能通过单日累计起降航班架次的形式逐日加以统计，只能通过更加灵活的调用数据库中跑道容量数据加以计算分析。但仅使用以上程序形式计算分析，则可能会造成变量E这一参数的取值长度难于把握，虽然已在初始阶段输入以天作为单位的时间长度，但若函数曲线处于长时间的有序递增或递减状态，这样的计算分析就会显得复杂、累赘，增加无效运算的次数，耗费空间资源。

实际编写过程中这是可以通过办法解决的，在原函数j＋＋的同时加入对运算次数n的讨论，调用次级函数如图4所示，通过人为规定的运算次数（程序中以3次为例）后仍无法找到波峰时，调整变量E的长度，依次递增一个先前量，并附值于变量E得出结果，原函数通过被附值后的变量E继续进行后计算，这样可以大大提高整个程序的工作效率。

次级函数的调用，使整个程序的内存使用和空间占有量更加合理，函数的传递计算方式更有层次。由于在原函数中未涉及变量E的长度计算，使得原函数的整个程序结构专注于梯度法优化的计算，次级函数则专注于变量E的长度计算，两个函数分别运用各自的初始设定、循环方式、参量计算，互不干扰，不仅让程序便于读写，也考虑到使用时间的推移、机场结构的变化、跑道流量的分配等因素，使程序升级更改修护工作更加便捷清晰，这也是在程序中使用函数调用的意义。

图4 二级函数f′（x）

2012年成都双流国际机场起降航班破23 万次，运用简单统计进行计算已经相当复杂，若想在全年当中找出跑道容量结构极值则更加困难。根据先前程序计算，调用数据库资料，则能轻易得出全年机场跑道容量结构极值，运算得出结果如图5所示，不难发现，整年的1月中旬～2月以及7月前后～10月中旬期间，出现两次较明显的波峰，在4月前后和11～12月期间，出现两次明显的波谷，说明机场跑道在这几个时间段内处于极值状态，从而得出双流机场跑道容量的结构分析。

图5 2012年航班起降架次

3 结束语

本文通过使用梯度法优化跑道容量结构的计算，其优势在于：①针对选取时间段较长，数据量繁多的统计，启到简化作用；②合理选取梯度递增长度，并通过人为设置，尽可能使运算变得简便、快速；③运算结果得出极值，波峰、波谷及其变化规律清晰明了；④梯度法计算用于民航相关统计计算较少，其研究发展空间巨大。

机场跑道容量结构的运算，可以清楚了解跑道使用的节奏快慢，使其在维护和修整的时间安排上，有了可以参考的时间段选取，对空中交通管制员的工作时间、人员人数分配起到参考作用，对空域容量、跑道运行能力评估有了更可靠的数据支持，为考量机场饱和度，扩建等问题提供了新的依据。目前，通过计算机成熟算法有针对性的使用在民航运输甚至整个交通运输产业中的实例还相对初级，这主要是由于交通运输的规模还在发展壮大中，运用简单的计算机运算方式已经可以解决绝大多数的统计分析问题，但随着民航产业的发展和城市规模的扩大化，今后的民航运输规模会出现几何倍增长，在这样一个大前提下，依然运用原有的运输手段、简单的统计分析方法去适应发展需求已不现实，只有通过先进的计算机算法理念和技术手段，数据统计分析在前，合理分配安排在后，才能有效改善运力与运输之间的关系。

［1］潘卫军.空中交通管理基础［M］.成都：西南交通大学出版社，2008.

［2］冯青川.机场管制［M］.成都：西南交通大学出版社，2007.

［3］张干宗.线性规划［M］.武汉：武汉大学出版社，2007.

［4］蒲会兰.内存概念在C 语言函数调用中的应用［J］.信息技术，2008（7）：109－111.

［5］孙建波.类C解释器中语法树及函数调用的研究与实现［J］.计算机与信息技术，2007（6）：85－87.

［6］陈宽明.机场容量评估研究 ［D］.成都：西南交 通大学，2007.

［7］丁毅萍.机场规划与运行分析［D］.南京：南京航空航天大学，2009.