高速公路基本路段交通运行状态评价

郎海鹏，付静静

（1.山西省交通科学研究院，山西 太原 030006；2.长安大学 公路学院，陕西 西安 710064）

迄今为止，高速公路交通运行状态在国内外尚无统一的定义，根据国内外学者研究现状，在不同的道路状况下驾驶员对于交通运行状态的心里感受是不同的，从客观上来解释，即交通流特征参数随着交通运行状态的变化而变化。现在比较通用的是采用美国《道路通行能力手册》中提出的服务水平来判定交通运行状态，并采用模糊的语言如“优”、“良”、“一般”、“较差”、“差”等对交通运行状态进行定性描述。

1 评价指标分析

高速公路交通系统是一个非线性、多维数、复杂可变的大系统，影响因素繁多，因此，传统的根据单一指标衡量高速公路交通运行状态的方法不够全面。例如，相同的交通流量往往对应着完全不同的交通运行状态。因此，应该采用多个指标进行全面科学的评价。

1.1 饱和度

对于已有的高速公路而言，其通行能力是固定的，饱和度是实际交通量与通行能力的比值，能准确的反映高速公路的负荷和拥挤状态，因此，将它作为高速公路基本路段交通运行状态的评价指标之一。

参考美国《道路通行能力手册》、《公路工程技术标准》（JTG B01—2003）及相关研究所的研究成果，给出基于饱和度的高速公路基本路段交通运行状态分级标准，如表1所示。

表1 基于饱和度的高速公路基本路段运行状态分级标准

1.2 车速

当有不良运行状态产生时，车速在反应交通变化上最为迅速和敏感，如果车速明显低于正常值时，表明该基本路段的交通处于拥挤状态。结合国内相关研究，并参考相关车速调查数据来确定基于车速的高速公路基本路段交通运行状态的分级标准，如表2所示。

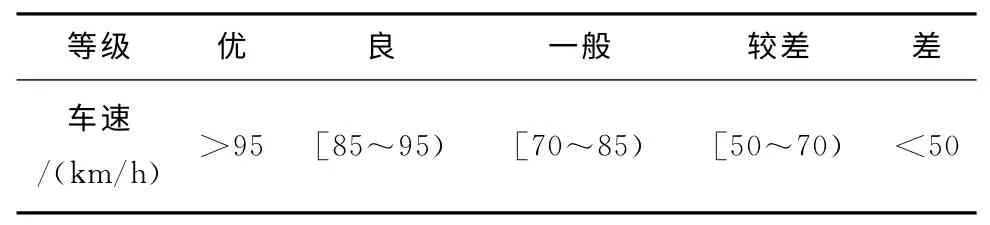
表2 基于车速的高速公路基本路段交通运行状态分级标准

1.3 空间占有率

据调查经验，当超音波检测器检测到的空间占有率上升到15%～25%时，高速公路上就会发生交通拥挤。因此，空间占有率对确定交通瓶颈和交通拥挤的地点具有指导作用，采用空间占有率作为评判标准之一能较好的判断高速公路基本路段交通运行状态。根据相关文献确定基于空间占有率的高速公路基本路段交通运行状态分级标准，如表3所示。

表3 基于空间占有率的高速公路基本路段交通运行状态分组标准

2 模糊综合评价法

模糊综合评价法最早由我国学者汪培庄提出的，是模糊数学的一种具体应用，具有数学模型简单的优点，对多因素、多层次复杂问题评价效果较好，成为近年来应用较多的评价方法之一。

2.1 模糊综合评价的基本步骤

1）建立高速公路基本路段交通运行状态评价指标集U＝｛X，Y，Z｝，其中X代表饱和度，Y代表车速，Z代表空间占有率。

2）建立高速公路基本路段交通运行状态评价集V＝｛v1，v2，v3，v4，v5｝，其中v1代表高速公路基本路段交通运行状态处于“优”，v2代表状态“良”，v3代表状态“一般”，v4代表状态“较差”，v5代表状态“差”。

3）建立高速公路基本路段交通运行状态单指标评价。如建立一个从U到X的模糊映射，此时指标集中的每个指标u与X，Y，Z的笛卡尔乘积X×中的元素（x，y，z）对应，则单指标评价矩阵为R，R，R＝［R1，R2，R3］T，即R1＝（r11，r12，r13，r14，r15），R2＝（r21，r22，r23，r24，r25），R3＝（r31，r32，r33，r34，r35），R1表示饱和度相对于状态优、良、一般、较差、差的隶属度，R2表示车速相对于状态优、良、一般、较差、差的隶属度，R3表示空间占有率相对于状态优、良、一般、较差、差的隶属度。评价矩阵为

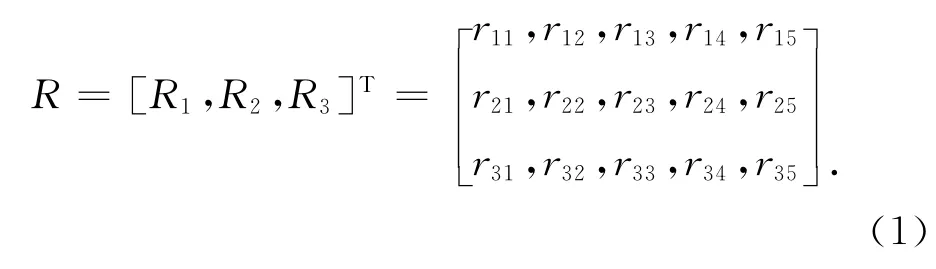
4）建立与指标相对应的权重集。在模糊数学综合函数的基础上建立模糊集W＝［w1，w2，w3］来表示每个指标的权重，常用的模糊综合函数有几何平均值、加权平均值、单因素决定性及多因素突出性。本文选择加权平均型，则w1代表饱和度所占的比重，w2代表车速所占的比重，w3代表空间占有率所占的比重，并满足w1＞0，w2＞0，w3＞0和w1＋w2＋w3＝1两个约束条件。

5）建立高速公路基本路段交通运行状态多指标综合评价集B

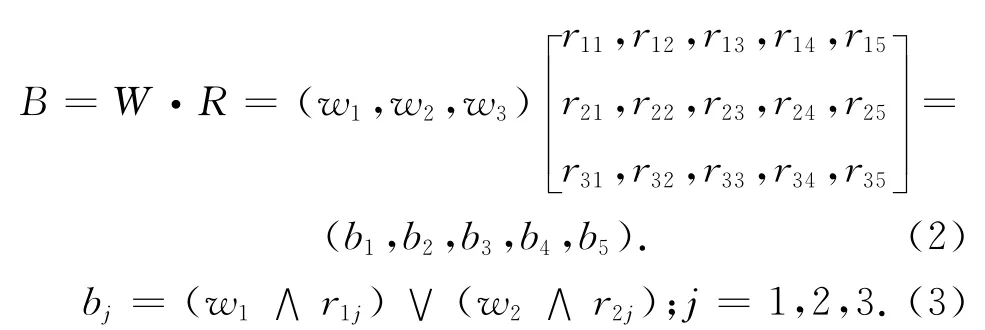
式中：“∧”为取大运算，“∨”为取小运算。其中b1，b2，b3，b4，b5分别为高速公路基本路段处于“优”、“良”、“一般”、“较差”、“差”状态的重要程度，max｛b1，b2，b3，b4，b5｝为评价的最终结果。

2.2 确定隶属度函数

隶属度函数的确定对于建立模糊综合评价模型来说至关重要，本文选取线性分析法，具体操作步骤为：确定一个连续的值域区间内具有分界效果的点，将某个指标的实际数值通过线性内插公式进行计算，即可得到其隶属度。例如，评价指标为空间占有率z，其隶属度函数为g（z），对各交通运行状态评价集的隶属度为g1（z），g2（z），g3（z），g4（z），g5（z）

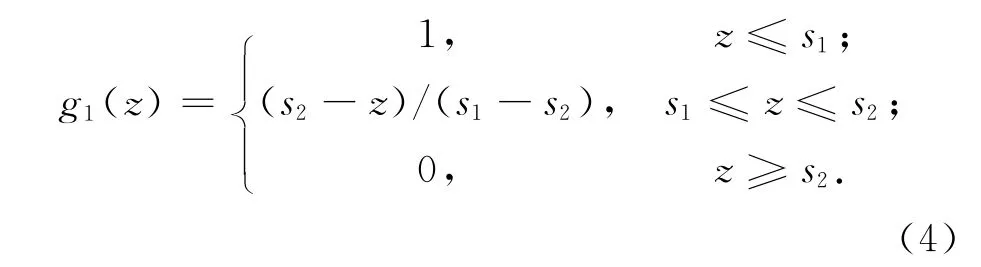
4 结束语

在本文中研究了一个供应商和制造商的供应链中的分级协调机制问题。根据其模型，运用模拟退火算法，提出求解该问题的一种求解方法。通过运用c＋＋对该问题进行了求解，得到了接近最优解的生产总成本最小，供应总利润最大的解，最后的算例证明了针对供应链角色，模拟退火算法是一种高效算法。但是，两个模型仅仅提供了解决在确定条件下供应商和生产商之间关系的框架，为了解决更广泛的问题，并求得更精确的解，还需对模型添加相应的决策变量和约束条件，或考虑有关模糊条件下的建模。

［1］林勇，马士华.供应链管理［M］.北京：高等教育出版社，2003.

［2］蔡连侨，陈剑.供应链建模与优化［J］.系统工程理论与实践，2001（6）：26－33.

［3］邢文训，谢金星.现代优化计算方法［M］.北京：清华大学出版社，2005.

［4］黄平，孟永钢.最优化理论与方法［M］.北京：清华大学出版社，2009.

［5］汪定伟，王俊伟，王洪峰，张瑞友，郭哲.智能优化方法［M］.北京：高等教育出版社，2007.

［6］何利英.面向客户的供应链优化模型研究［D］.成都：西南交通大学，2003.

［7］孙文瑜，袁亚湘.最优化理论与方法［M］.兰州：科学出版社，1997.

［8］张文修，梁怡.遗传算法的数学基础［M］.西安：西安交通大学出版社，2003.