基于模拟退火算法的供应链协调机制问题

朱美桦，王兴芳，韩 瑛

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

1 供应链中分级协调机制的问题阐述和模型建立

1.1 问题描述

图1为库存系统图，图中箭头方向表示物流的方向，有向线段表示销售商、供应商、生产商之间的物流。

图1 供应调查

为了满足销售商的要求，生产商需从供应商那里提前订购零件，但由于种种原因，有时供应商不能按时交货，这样产品就不能按时被生产商生产出来，进而影响了销售商的销售市场。但是，任何事物都是有规则的，供应商、生产商、销售商也不例外，为了彼此达到“互利共赢”的目的，一张合同将它们紧密联系在了一起。

因此，为了协调这种关系，提出方法—惩罚费用。对于供应商不能按时交货，给出惩罚费用，对于生产商不能按时交货，也给出一个惩罚费用。

1.2 供应链的基本数学模型

1.2.1 模型假设

本文所做的假设如下：①生产商和供应商是长期的合作伙伴，并且相互信任；②生产商和供应商信息不对称，也就是说，他们之间保持一定的隐私，不透漏其所有数据；③供应商、生产商和销售商是一个相互合作的团队，所有参与者都为了使一个共同的目标得到最优化；④在整个供应链中，已知的量是销售商订单；⑤在整个供应链中，只考虑成本不考虑时间，供应商的模型是线性的；⑥零件费用相等；⑦零件最大供量应该相同。

1.2.2 模型建立

1.2.2.1 生产商的模型（P）

假设供应链中有i∈（i＝1，2，…I）个零件，j∈（j＝1，2，…，J）作业。在计划期t∈（t＝1，2，…T）内，按定单满足客户产品量和时间需求。

1）目标函数

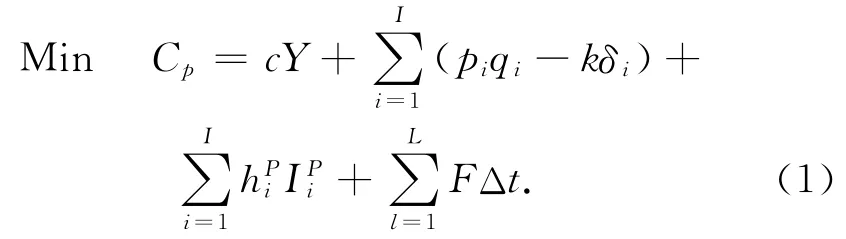
2）约束条件

生产力约束

网络约束

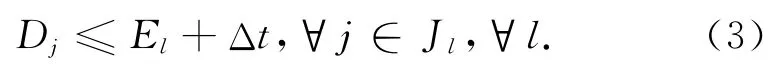
物质平衡约束

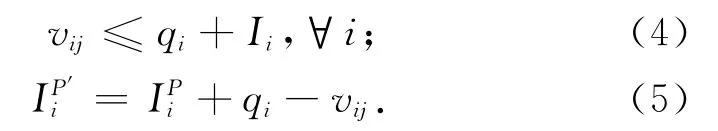
订单交货约束

整数约束

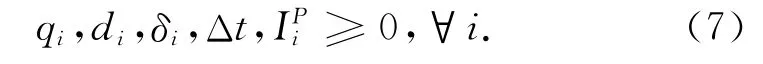
3）参数和变量

参数：i为零件，j为作业，t为时间，I为总零件数，J为总作业数，c为生产力单位成本，Y为单周期最大生产力，Pi为购买单个零件i的费用，hpi为生产商对零件i的单位库存成本，Δt为延期时间，F为延期交付的单位惩罚费用（P→C），k为延期交付的单位惩罚费用（S→P）。

变量：qi为购买零件i的数量，Ipi为生产商对零件i的库存量，ei为延期交付零件i的数量（S→P），di为要交付零件i的数量（S→P），aj为作业j的生产消耗，Dj为作业j的生产持续时间，Ei为预期交付时间（P→C），vij为开始作业j需要的零件量i。

从上面可以看出：生产商的模型为总成本最小，它包含存储费用、购买费用和惩罚费用。

1.2.2.2 供应商的模型（S）

1）目标函数

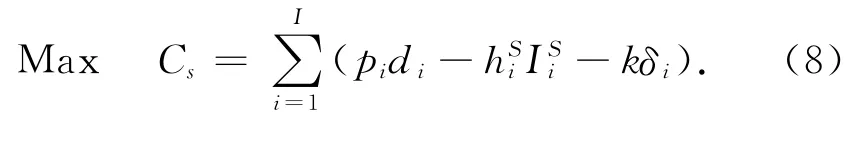
2）约束条件

物质平衡约束

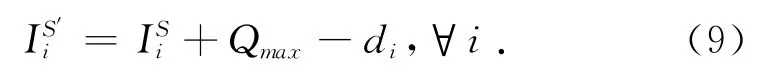
订单交货约束

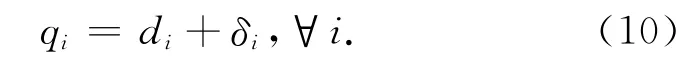
整数约束

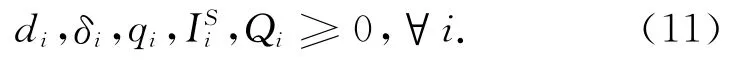
3）参数和变量

参数：pi为购买单个零件i的 费用，hsi为供应商对零件i的库存成本，k为延期交付的单位惩罚费用（S→P），Qi为零件i的最大供应量。

变量：di为要交付零件i的数量（S→P），Isi为供应商对零件i的库存量，ei为延期交付零件i的数量（S→P）。

从上面可以看出：供应商的模型为总利润最大，它也包含购买费用、存储费用和惩罚费用。

2 模拟退火算法及求解

2.1 模拟退火算法的基本流程

根据模拟退火算法的基本框架，针对具体问题时还需要具体的设计。模拟退火具有两层循环，内循环模拟的是在给定的温度下系统达到平衡的过程。在此循环中，每次从当前i的领域中随机找出一个新解j，然后按照Metropolis的准则概率接受新解。算法中的random（0，1）是指在区间［0，1］上按均匀分布产生一个随机数，而所谓的内层达到热平衡也是一个笼统的说法，可以定义为循环一定的代数，或者基于接受率定义平衡等。算法的外层循环是一个降温的过程，当在一个温度下达到平衡后，开始外层的降温，然后在新的温度下重新开始内循环。降温的方法可以根据具体问题具体设计，而且算法流程图中给出了初始温度T 也需要算法的使用者根据具体的问题而制定。

在用模拟退火算法求解最优化问题时，涉及以下几个方面的基本要素。

2.1.1 初始温度

影响模拟退火算法全局搜索性能的重要因素之一是初始温度t0的设置。实验表明，要获得高质量解，初温就得越大，但花费的计算时间也将越多。因此，初温的确定应折中考虑优化效率和优化质量，常用方法有以下几种：

1）以个状态目标值的方差为初温，均匀抽样一组状态；

2）利用经验公式给出初温；

3）随机产生一组状态，确定出两两状态间最大目标差值｜△max｜，然后根据差值，利用一定的函数确定初温。例如t＝－△max／pr，其中pr为初始接受概率。

2.1.2 领域函数

领域函数（状态产生函数）通常有两部分组成，即候选解产生的概率分布和产生候选解的方式。概率分布可以是均匀分布、指数分布、正态分布等，候选解一般采用某一概率密度函数对解空间进行随机采样获得。

2.1.3 接受概率

指从一个可行解Xk向另一个可行解Xnew的转移概率，通俗的理解是接受一个新解为当前解的概率。与它有关的是当前的温度参数tk，随着温度的下降而减小。一般采用Metropolis准则。

2.1.4 冷却控制

指的是降温管理表（降温方式）即从某一较高温的状态t0向较低温状态冷却。假设用tk来表示时刻k的温度，则经典模拟退火算法的降温方式为

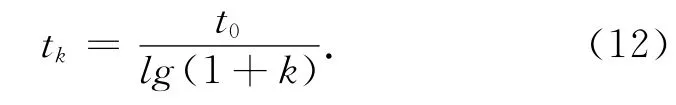
而快速模拟退火算法的降温方式为

这2 种方式都能使模拟退火算法收敛于全局最小点。

2.1.5 内层平衡

内层平衡也称Metropolis抽样稳定准则，相当于由各温度下产生候选解的数目决定。以下几项是常用的抽样稳定准则：预先设定的抽样数目，内循环代数；目标值变化较小（连续若干步）；目标函数的均值是否稳定。

2.1.6 终止条件

常用的算法中止准则包括以下几项：外循环迭代次数；终止温度的阀值；连续若干步保持不变直到算法搜索到最优值；检验系统熵是否稳定。

2.2 模拟退火算法的描述和实现

2.2.1 一般过程描述

模拟退火的一般过程可以描述为：

步骤1 给定初温Tk＝T0，随机产生初始生产顺序向量（di，ei，I0p）＝（d0，e0，Ip0），计算目标值Cp。令k＝0。

步骤2 如果停止准则不满足，重复以下过程。

步骤2.1 执行以下过程Lk次：

步骤2.1.1 从状态i的领域解中随机选取新状态j；

步骤2.1.2 令Δ＝f（j）－f（i）；

步骤2.1.3 若△＜＝0，则令i＝j，否则以概率exp（－△／tk）令i＝j。

步骤2.2 退温：令k＝k＋1，计算tk＝d（tk），同时按规则更新Lk。

步骤3 输出i。

2.2.2 参数设定

根据模拟退火算法的演算流程，表1是对模拟退火算法的参数设定。

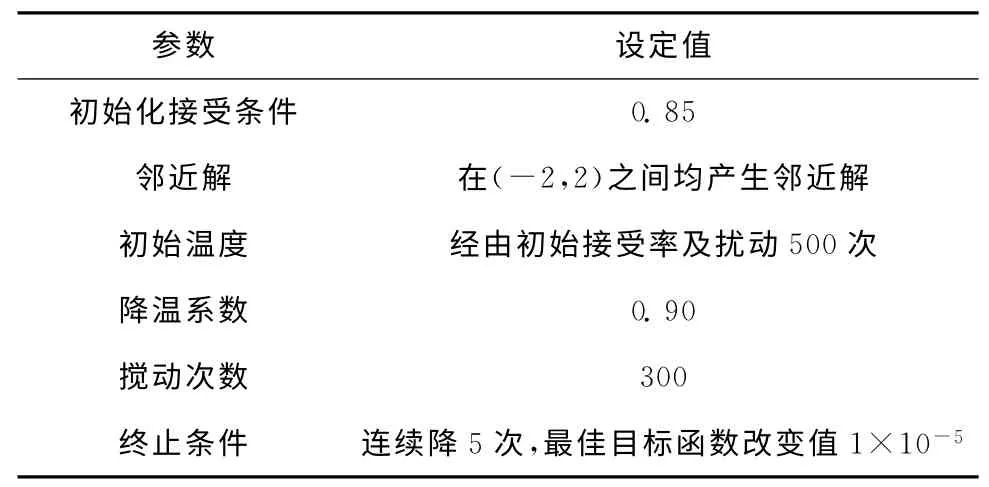
表1 模拟退火算法的参数设定

3 实 例

为了说明该算法的有效性及可靠性，而且能够直观反映出一些模拟退火特征，实验结果如表2～表4所示。

假设整个供应链中有7个作业，7个订单，其中一个订单对应一个作业。

表2 订单数据和作业在第一阶段的生产消耗

表3 生厂商的数据

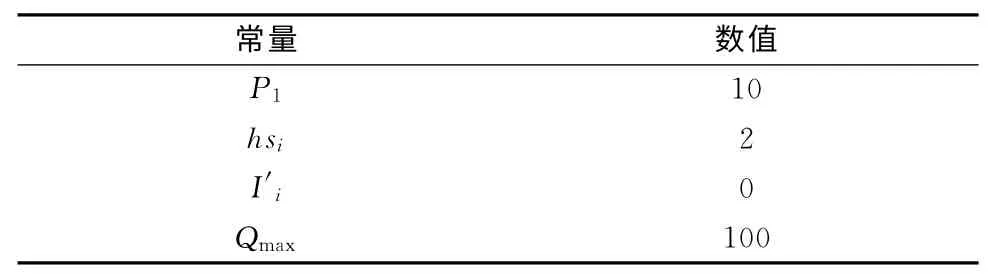
表4 供应商的数据

4 结束语

在本文中研究了一个供应商和制造商的供应链中的分级协调机制问题。根据其模型，运用模拟退火算法，提出求解该问题的一种求解方法。通过运用c＋＋对该问题进行了求解，得到了接近最优解的生产总成本最小，供应总利润最大的解，最后的算例证明了针对供应链角色，模拟退火算法是一种高效算法。但是，两个模型仅仅提供了解决在确定条件下供应商和生产商之间关系的框架，为了解决更广泛的问题，并求得更精确的解，还需对模型添加相应的决策变量和约束条件，或考虑有关模糊条件下的建模。

［1］林勇，马士华.供应链管理［M］.北京：高等教育出版社，2003.

［2］蔡连侨，陈剑.供应链建模与优化［J］.系统工程理论与实践，2001（6）：26－33.

［3］邢文训，谢金星.现代优化计算方法［M］.北京：清华大学出版社，2005.

［4］黄平，孟永钢.最优化理论与方法［M］.北京：清华大学出版社，2009.

［5］汪定伟，王俊伟，王洪峰，张瑞友，郭哲.智能优化方法［M］.北京：高等教育出版社，2007.

［6］何利英.面向客户的供应链优化模型研究［D］.成都：西南交通大学，2003.

［7］孙文瑜，袁亚湘.最优化理论与方法［M］.兰州：科学出版社，1997.

［8］张文修，梁怡.遗传算法的数学基础［M］.西安：西安交通大学出版社，2003.