基于改进Vague集的智能一次设备评估

胡元潮，谢齐家 ，阮江军，安韵竹 ，黄 涛，龚若涵 ，李志政

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.湖北省电力公司电力试验研究院，湖北 武汉 430077；3.合肥电力公司，安徽 合肥 230000）

0 引言

智能电网为我国电网中长期的发展方向，其绩效目标、性能特征、关键技术与功能实现等方面的要求是评价智能电网发展水平的关键所在［1-4］。变电站作为电网基础运行数据的采集源头和命令执行单元，逐步完成由传统变电站到数字化变电站再到智能变电站的转变和升级，已成为当前智能电网建设的重点方向。自2010年开始，囯网公司进行大量的研究工作，陆续启动了智能变电站改造项目，其中第一批智能变电站试点工程建设已基本完成［5-6］。为配合国网公司二期智能站改造试点工程，除对智能站整体改造水平评估外，需要具体到单一设备智能改造水平的横向对比评估。此外，考虑到在对具体设备进行评估时，各智能站之间差异性较大，模糊因素较多，在评估算法上应充分考虑模糊因素的量化问题。

Vague集理论是模糊集的一种推广形式，自Cau和Buehrer于1993年提出以来，已取得较快发展［7-8］。传统多目标决策理论如AHP、熵权法、灰色关联法、TOPSIS等方法在不确定信息描述上有欠缺［9-11］。与模糊集理论相比，Vague集理论数学表征和处理的不确定性信息更为丰富。因此Vague集理论在模糊控制器设计、多目标模糊决策、人工智能等方面取得了很好的应用，但电力行业对此理论方法涉及较少。

本文将Vague集理论运用到变电站一次设备的智能改造综合评估中，并对Vague集理论一致性检验及权重求解作了改进。结合文中提出的变电站具体设备的智能改造评估模型，对几个试点项目的智能设备改造情况进行评估。最后结合实际算例具体说明该方法的计算流程，并对比了其他评估方法，说明了该方法的实用性及优势所在。

1 变电站智能改造评估模型的建立

智能变电站采用集成智能设备，完成信息的采集、测量、控制、保护、计量和监测等功能，并实现电网实时在线分析与决策，保证电网的协同互动运行。在国家电网第一、二批的智能变电站建设中，变电站重要一次设备智能组件的集成度以及监测信息的高级应用，是试点工程变电站智能改造水平的集中体现。

针对改造完成及建设中的智能变电站完成情况，国网公司先后组织高压测试及设备学组的部分专家，对一次设备智能改造一、二期试点工程项目进行调研和评估。评估采用从整体到部分的分层评估决策原则：选定待评估的变电站，对站内一次设备如变压器、GIS（HGIS）组合设备、断路器等进行整体评估，继而根据准则中电气设备智能组件的要求［12-13］，对每种设备的监测类别进行细化（如变压器的油温、局部放电等）。

实际调研表明，不同电压等级的变电站对一次设备智能改造的区别基本上限于改造难度和不同智能组件生产厂家的方案上。同一个变电站的不同设备按照技术导则要求，智能组件的安装虽有区别，评估指标基本可从测量、控制、通信等要求统一恒定［14］。本文从一次设备的智能改造角度出发，提出一次设备智能改造水平评估体系模型，对变压器、GIS组合设备、互感器、开关、避雷器及电缆等主要高压一次设备的改造进行评估，评估指标体系如表1所示。

2 改进Vague集多目标评估算法流程

Vague集作为模糊集的推广，最大优点是兼顾了隶属度、非隶属度和踌躇度（不确定度）三方面的信息，比传统的模糊集表征模糊信息的能力更为灵活和丰富。

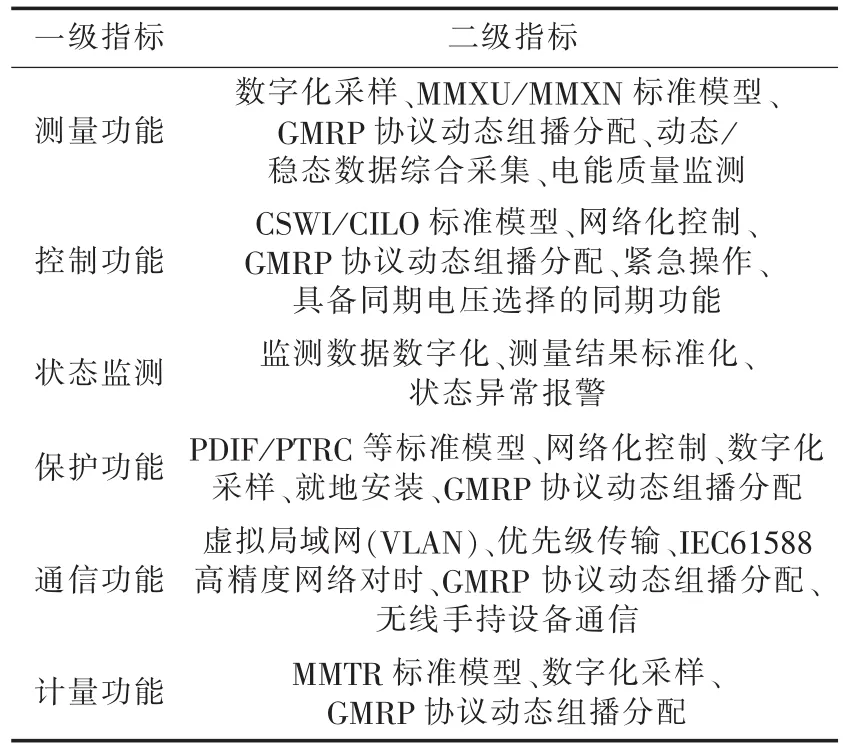
表1 变电站一次设备智能改造水平评估指标体系Tab.1 Evaluation index system for substation retrofitting with intelligent primary equipment

2.1 Vague值判断矩阵

根据Vague集定义，论域X（域中任意元素用x表示）上的Vague集v用真隶属度函数tv和假隶属度函数fv表征：

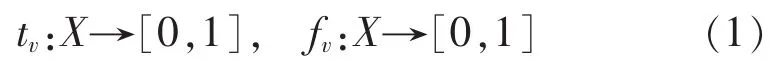
假设 tv（x）和 fv（x）分别表示支持和反对 x 的证据所导出的隶属度下界，且 tv（x）+fv（x）≤1，则元素 x在 Vague 集 v 上的隶属度被［0，1］上的子区间［tv（x），1-fv（x）］所界定。根据上述定义，支持 xϵX 的必要性用 tv（x）表征，支持 xϵX 的可能性用 1-fv（x）表征，而1-tv（x）-fv（x）数学描述了对 x 的不确定度。

设 X=｛x1，x2，…，xn｝是一属性集，决策者利用 0.1～0.9标度法［15］对每个属性两两比较，这就构成了基于Vague 值的判断矩阵 V=［Vij］m×n，其中 Vij=［tij，1-fij］为Vague值，tij和fij分别表示决策者对属性xi和xj的偏好程度，1－tij-fij表示决策者的不确定度，根据判断矩阵结构性质，有 tijϵ［0，1］，fijϵ［0，1］，tij+fij≤1，对角线元素满足tii=fjj=0.5，非对角线元素满足互补性：tij=fji。在实际评估中，不同专家对某一属性的判断往往具有主观性和各异性，因此可以取不同决策者评估值的均值作为判断矩阵的Vague值。

2.2 Vague值判断矩阵的模糊逼近

Vague集在多目标评估时一般只考虑了支持和反对隶属度，对不确定信息的考虑不够。事实上，不确定信息作为决策者的态度之一，应当充分细化挖掘。另外，以vague值作为判断矩阵的元素使计算复杂度增加。基于这两方面的考虑，将Vague集转化为模糊集是处理vague值判断矩阵的可行方法。

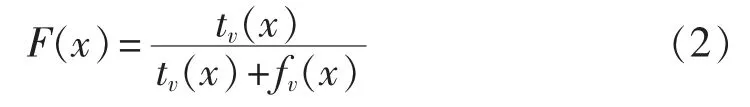
同样，推广到Vague值判断矩阵的模糊逼近，可以得到 V 的模糊逼近判断矩阵 Q=［qij］n×n，其中 qij见式（3）。

2.3 模糊判断矩阵的一致性检验及修正

在模糊判断矩阵的一致性检验问题上，文献［15-16］考虑了判断顺序的传递性，避免了在各属性优劣循环链中出现诸如xi≺xj≺xk≺xi的判断顺序逻辑矛盾，但该方法忽视了偏差的可接受性；文献［17］虽设定了偏差阈值，但对判断顺序的传递性考虑不够。事实上，模糊判断矩阵需要同时满足一致相容性和逻辑传递性。本文结合2个特性提出综合检验标准并给出修正方法，使一致性检验更为合理。

2.3.1 相容性指标验证

模糊判断矩阵 Q 满足互补条件，对∀kϵ（1，n），有qij=0.5+qik-qjk，则矩阵Q为完全一致性矩阵。实际评估中，因决策信息的各异性，完全一致性矩阵很难存在，需要通过修正不断逼近。通常用一致性指标CI衡量偏差程度（一般取到 0.1 以下）。称为Q的特征矩阵，其中如式（4）所示。

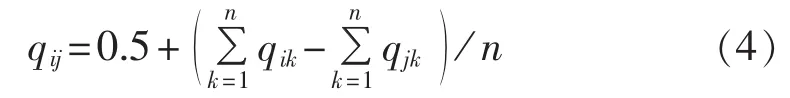
相容性指标CI用模糊判断矩阵Q与其特征矩阵Q*的偏差表示为：

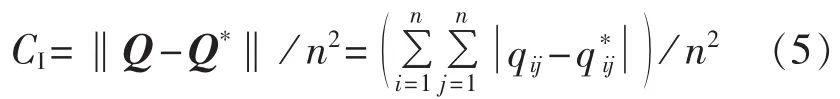
其中，“‖·‖”表示范数。

一般实际运用中，当 CI＜ε（0.10≤ε≤0.15）时，可认为Q为满意一致矩阵。

2.3.2 传递性指标验证

引用图论中的可达矩阵T验证模糊判断矩阵Q的逻辑传递性［18］。定义矩阵QT为模糊判断矩阵Q的伴随可达阵，当 qij＞0.5 时，QT的取值为“真”，并用1表示；反之视为“假”，用0表示。依次求解伴随可达阵的n阶次，得到可以判断Q一致性的可达矩阵T为：

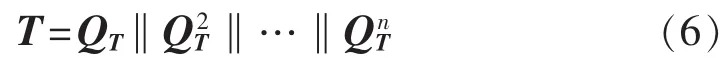
其中，“‖”为布尔运算中的“或”运算。若可达矩阵T所有主对角线元素为0，认为Q满足逻辑传递性的一致检验。

2.3.3 综合检验及修正

当Q同时满足相容性指标和传递性指标时认为其一致性是可接受的，否则需要对偏差过大的列进行修正。计算每行元素偏差值之和：

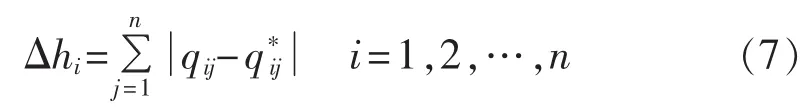
选取偏差最大的第h行元素进行第k次修正：

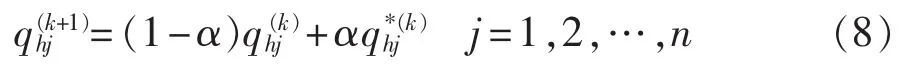
其中，0≤α≤1为原始矩阵信息所占的比例。

同理，对偏差最大的第l列元素进行修正：

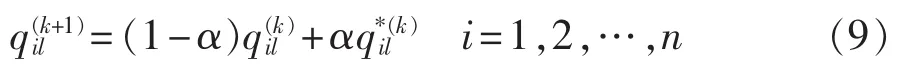
每次修正后对矩阵Q进行一致性检验，直至同时满足相容性指标和传递性指标为止。

2.4 求解评估指标权重

对符合一致性检验的矩阵Q进行分层权重求解。利用特征向量法求出Q的最大特征值λmax和对应该特征值的特征向量。将特征向量进行归一化处理得到第k层n个指标的权重向量计算评估指标对于总目标的综合权重 w=（w1，w2，…，wn）。

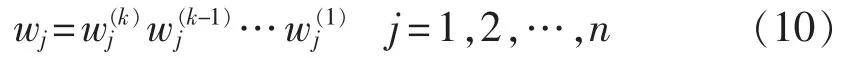
2.5 求解综合评估结果

对于m个对象、n个指标的评估，构造加权决策矩阵 Y=（yij）m×n，其中，yij由不同评估对象各指标的专家评估值或实际参数值乘以该指标权重确定（注意对效益型参数和成本型参数［8］的归一化处理）。加权决策矩阵可以直观地表示各评估对象之间的指标对比情况。实际中一般取一级评估指标zj作为决策矩阵 Z=（zij）m×n的列向量，其中 zij如式（11）所示。

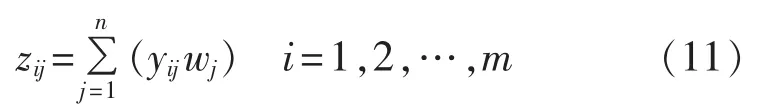
根据加权决策矩阵得到各评估对象的最终评估值 ηi为：

2.6 Vague集评估方法流程图

利用Vague集评估方法对实际对象进行评估时，可遵循上述评估步骤，具体流程图如图1所示。

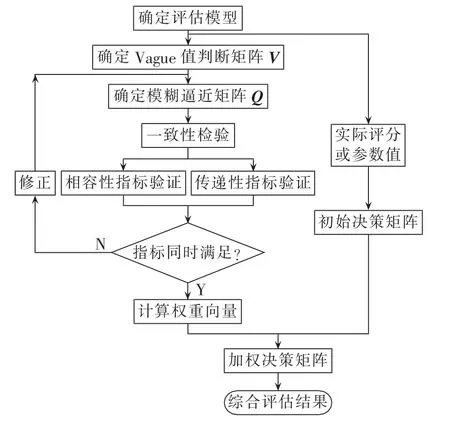
图1 Vague集评估方法流程图Fig.1 Flowchart of evaluation based on Vague sets

3 算例分析

3.1 实际算例

选取试点工程中改造初步完成的变电站主要一次设备作为评估对象，以改造完成的几座110 kV智能变电站试点工程为例，选取3个站的变压器、2个站的GIS高压组合电器设备作为评估对象。以表1评估指标体系对每种一次设备的智能化改造水平进行评估。首先对一、二级指标利用Vague集评估方法求解每级指标的权重向量，以第2层指标为例，取不同专家对二级指标Vague值的均值构成Vague值判断矩阵如式（13）所示。

利用式（2），求Vague值判断矩阵的模糊逼近矩阵Q，并按式（4）、（5）对矩阵进行相容性指标验证，得CI=0.0458，满足相容性偏差要求。按式（6）验证Q的传递性，可达矩阵主对角线元素不全为0，因此对偏差最大的第6行、第6列按α=0.4进行修正。2次修正后，得到最终的模糊判断矩阵见式（14）。

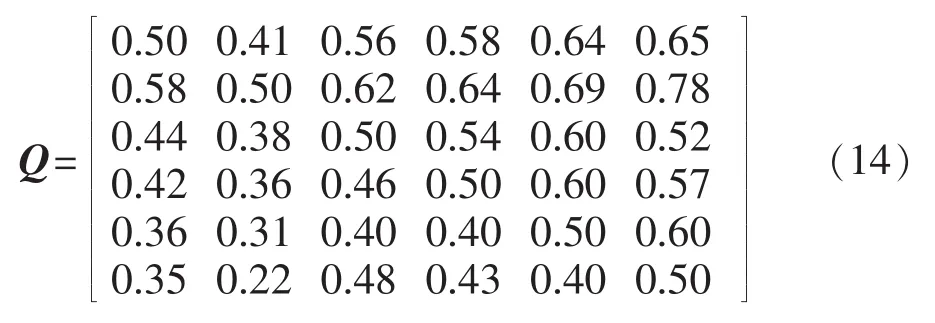
经修正，传递性指标达到要求，CI=0.0228，可见相容性偏差也得到修正。依次求解各二级指标的Vague值判断矩阵并进行模糊逼近和一致性判断，求解结果见表2，Y、N分别表示满足和不满足一致性判断。

根据修正后的模糊判断矩阵，利用特征向量法得到一级指标权重向量（0.1866，0.2133，0.1661，0.1614，0.1416，0.1310）。同理，根据各个二级指标的模糊判断矩阵求解对应权重向量，由式（10）求得二级指标综合权重向量如表3所示。

选择待评估的变电站一次设备，对每个设备智能改造评估的二级指标（表1）进行评分。其中，支持和反对某指标完成水平的评分分别为tv（x）和fv（x）（评分 tv（x）+fv（x）≤1），则对该指标的评分构成一个Vague 值［tv（x），1-fv（x）］，根据式（2）取该指标的模糊逼近值作为该指标的实际评分值。不同决策者对某一指标的Vague值评定各有差异，取每个二级指标模糊逼近值的平均值构成该设备的评分向量以对变压器A的评分向量求解为例，经过专家根据表1的评定，变压器A的评分结果见表4。

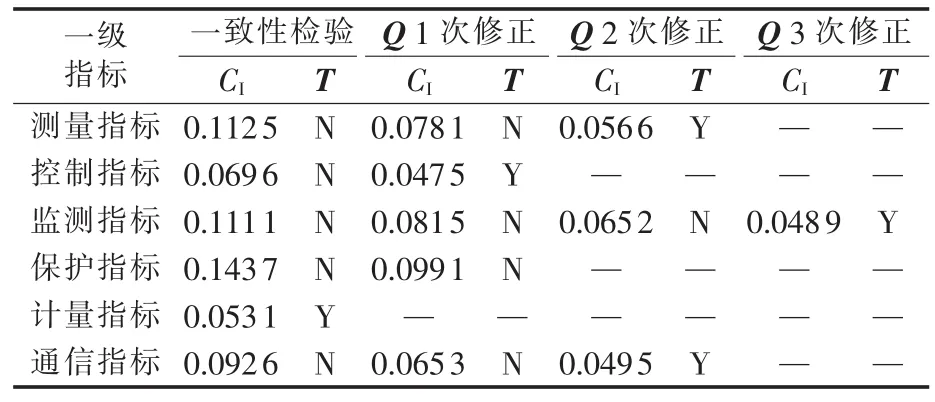
表2 二级指标Vague集矩阵求解及一致性检验结果Tab.2 Solutions of secondary index Vague set matrix and results of consistency inspection

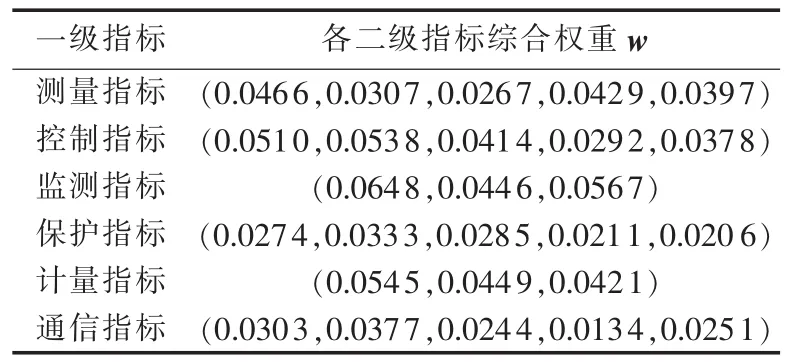
表3 二级指标综合权重向量结果Tab.3 Solutions of secondary index comprehensive weight vectors

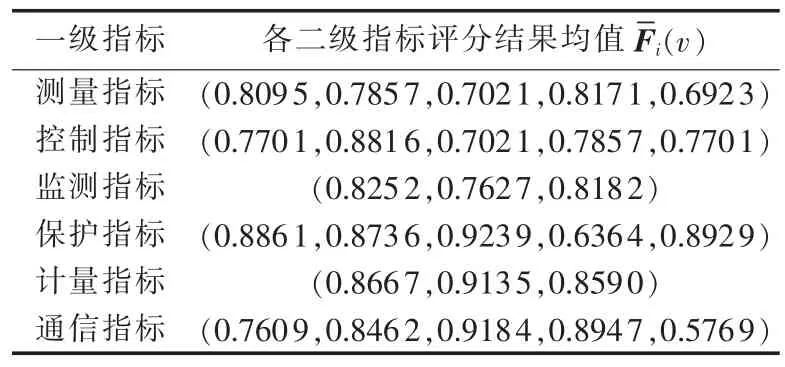
表4 基于Vague值的变压器A的评分结果Tab.4 Results of evaluation based on Vague value for transformer A

依次计算其他一次设备的评分结果，并根据式（11）组成决策矩阵Z。各智能一次设备的评估指标的加权值如表5所示。

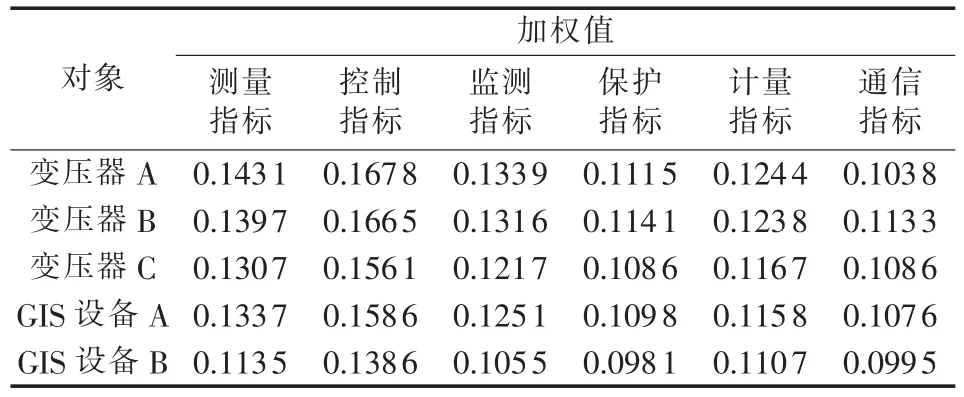
表5 各智能一次设备的评估指标加权值Tab.5 Weighted evaluation indexes for differentintelligent primary equipments

由式（12）可以得到各一次设备智能改造综合评估结果如表6所示。同时，表6给出了利用AHP［9］和 TOPSIS 法［19］的计算值。由于不同评估方法采用的计算步骤不同，最后的评估值会有差异，但不同评估方法的排序结果是一致的。

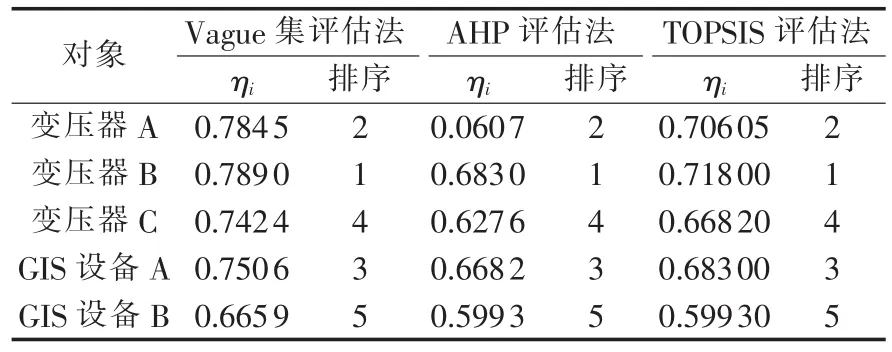
表6 各一次设备智能改造综合评估结果Tab.6 Evaluated results of intelligent primary equipments

3.2 评估结果分析

评估结果表明：变压器作为变电站中主要电力设备，在智能改造过程中，一般对变压器的智能改造要优于其他一次设备；新建智能变电站按照智能变电站标准建设，其一次设备智能化水平高于其他改造变电站。算例中GIS设备A的评估值高于变压器C，这是由于GIS组合电器设备A所在变电站是新建智能变电站，而变压器C所在变电站为后期改造变电站，评估结果与实际试点工程切合。

从不同评估方法的结果来看，Vague集评估方法引入不确定度对模糊数据进行数学表征，因此可以更合理地表征人为因素，对于水平相近的评估对象区分度更高，与实际工程更加相符。

4 结语

本文利用Vague集理论解决变电站一次设备智能改造的评估问题。首先根据相关标准和调研信息构建评估模型，并对Vague集评估算法进行了改进，使评估方法更合理、准确。文中利用该评估方法对变电站的部分一次设备的智能改造水平进行评估，并给出实例验证。运用该法进一步对智能变电站整体智能改造水平以及区域电网智能电网的整体水平进行评价是下一步的工作目标。本文评估可为变电站智能改造和电网制定相应的标准提供现实依据。