具有变系数梯度项的半线性椭圆型方程组解的存在性问题＊

任相霞

（中国海洋大学数学科学学院，山东 青岛266100）

0 引言

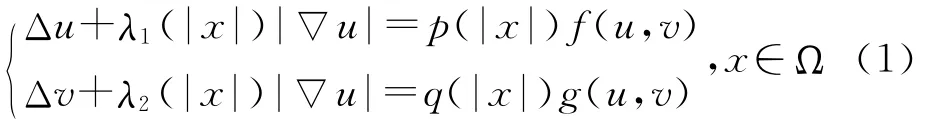
的解的存在性与不存在性。其中Ω是Rn（n≥3）中的有界区域或整个Rn空间，f，g∶［0，∞）×［0，∞）→［0，∞）是关于2个变量都是非负不减的连续函数；加权系数p（x），q（x）为非负连续函数且满足c－positive条件，梯度项系数λi（x）≥0（i＝1，2）是连续函数。

近年来，关于半线性椭圆型方程（组）边值问题的解的存在性、唯一性及渐近性等方面的研究得到了令人瞩目的成就［1－6］，尤其是关于半线性椭圆型耦合方程组边值问题的解的存在性、唯一性及渐近性行为等方面的研究得到了较快的发展［7－11］。文献［7－8］研究了方程组（1）不带梯度项且f（u，v）＝vα，g（u，v）＝uβ或f（u，v）＝f（v），g（u，v）＝g（u）时全局径向大解及有界全局解的存在性问题。当方程组（1）带常系数梯度项且系数为常数1时，文献［9］研究了在整体Rn空间上或者一个有界区域 Ω 上f（u，v）＝f（v），g（u，v）＝g（u）时整大解和大解的存在性与不存在性。文献［10］研究了在整体Rn空间上方程组（1）带常系数梯度项且系数为常数1时整大解的存在性与不存在性问题。文献［11］中作者对包含梯度项且带加权系数的单个方程）的全局正解的存在性进行了研究，并且得到了整大解存在的充分必要条件。受上述文献启发，本文研究包含变系数梯度项的半线性椭圆型耦合方程组解的存在性问题，利用径向

本文考虑包含变系数梯度项的半线性椭圆型耦合方程组解方法、极值原理和反证法相结合得到有界全局正解和整大解存在的充分必要条件及大解和整大解不存在的充分条件，找到了梯度项的加权系数对方程组解的影响。

1 预备知识及主要结论

首先给出2个相关定义。

定义1 设（u，v）是方程组（1）的解。若Ω为有界区域且满足当x→ЭΩ时，有u（x）→∞及v（x）→∞，则称（u，v）是方程组（1）的大解。若Ω为整体空间Rn且满足当｜x｜→∞时，有u（｜x｜）→∞，v（｜x｜）→∞，则称（u，v）是方程组（1）的整大解或者全局大解。特别的，x∈Ω，当u（x）＞0，v（x）＞0时，这样的大解称为全局正解。

为描述简便，下文中记用反证法易证必要性。定理2的证明

假设方程组（1）存在大解（u，v），定义u，v在球上的平均值函数：

其中：v0（sn－1r）是n－1维球的体积；σr是球的测度。易得当中梯度项的存在，导致无法判断u珔的单调性。为了避免这些问题，令

易知，U＞0，V＞0的不减函数，且当r→∞时，U（r）→∞，V（r）→∞。由条件（2）可知，存在常数 M＞0，使得当s＋t≥1时，f（s，t）≤M（s＋t）；g（s，t）≤M（s＋t）；当0≤s＋t＜1时，f（s，t）≤M，g（s，t）≤M。

同理，

由（9）、（10）相加得

由U，V的有界性知u，v也是有界的，这与假设u，v是大解矛盾，因此方程组（1）不存在大解。

定理3的证明

利用反证法。不妨设方程组（1）存在正大解（u，v）。令

则当x→ЭΩ时，由u→∞，v→∞知w→∞。

对（11）通过计算有因此，对所有的x∈Ω，Δ（w－A｜x｜2）＜0。

再令z（x）＝w（x）－A｜x｜2，x∈Ω，即x∈Ω，Δz＜0；且当x→ЭΩ时，z（x）→∞。

致谢：在该论文的写作过程中，始终得到了导师朴大雄教授的悉心指导，在此，谨向朴老师致以崇高的敬意和真挚的感谢。

［1］ Dalmasso R.Existence and uniquess of positive solutions of semilinear elliptic systems［J］.Nonlinear Anal，2000，39（5）：559－568.

［2］ De Figueiredo D G，Jianfu Y.Decay，symmetry and existence of solutions of semilinear elliptic systems ［J］.Nonlinear Anal，1998，33（3）：211－234.

［3］ Wang X，Wood A W.Existence and nonexistence of entire positive solutions of semilinear elliptic systems［J］.Math Anal Appl，2002，267（1）：361－368.

［4］ Ghergu M，Niculescu C，Radulescu V.Explosive soultions of elliptic equations with absorption and nonlinear gradient term ［J］.Indian Academy of Sciences.Mathematical Sciences，2002，112（3）：441－451.

［5］ Lair A V，Shaker A W.Entire solution of a singular semilinear elliptic problem ［J］.Math Anal Appl，1996，200（2）：498－505.

［6］ Serrin J，Zou H.Existence of positive entire solutions of elliptic Hamiltonian systems［J］.Comm Partial Differential Equations，1998，23（3－4）：375－398.

［7］ Lair A V，Wood A W.Existence of entire large positive solutions of semilinear elliptic systems［J］.Differential Equations，2000，164（2）：380－394.

［8］ Cirstea F，Radulescu V.Entire solutions blowing up at intinity for semilinear elliptic systems ［J］.Math Pures Appl，2002，81：827－846.

［9］ Ghergu M，Radulescu V.Explosive soultions of semilinear elliptic systems with gradient term［J］.Rev R Acad Cienc ser A Mat，2003，97（3）：467－475.

［10］ Zhang Xingguang，Liu Lishan.The existence and nonexistence of entire positive solutions of semilinear elliptic systems with gradient term ［J］.Math Anal Appl，2010，371（1）：300－308.

［11］ Fatem Toumi.Existence of blow－up solutions for nonlinear problems with a gradient term ［J］.Interentional J of Mathematics and Mathematical Sciences，2005，（7）：1－11.

［12］ Cheng K S，Lin J.On the elliptic equationsΔu＝K（x）uσandΔu＝K（x）e2u［J］.Trans Amer Math Soc，1987，304（2）：639－668.