海啸数值预报模型研究进展＊

鲍献文，褚芹芹，于华明

（中国海洋大学海洋环境学院，山东 青岛266100）

海啸作为1种自然灾害，在过去20年中，世界范围内已发生了212次，引发灾难的有19起之多。2011年3月11日，日本本州岛仙台港以东发生了9.0级特大地震，引发了大规模海啸，冲毁了沿岸建筑，最为严重的是福岛核电站受到了破坏，放射性物质随着海水、大气开始扩散，引发了邻近各国的恐慌，也让人们继2004年12月26日那次触目惊心的印尼大海啸之后，深深地记住了“海啸”这个灾难性的名词。

造成海啸的本质原因是海底地震或水下滑坡造成海底运动，这种扰动激发海面波动，向四周传播，即形成海啸。海啸在大洋中传播时速度非常快，一般在500～1 000km／h。随着海啸向岸边传播，由于水深的减小，其传播速度逐渐减小，同时海啸波高也随水深的减小而显著增加。然而并不是所有的地震都能引发破坏性海啸，需要具备几个必要条件：（1）引起海啸的海底地震震源较浅，一般要小于40km，震级一般在6.5级以上；（2）海底必须有大面积垂直运动；（3）发生地震的海区要有一定水深，一般水深都在1 000m以上［1］。

海啸带来的严重后果早已引起了全世界的关注，为了减轻海啸再次给世界带来巨大的灾难，研究有效的海啸预报系统是解决该问题的有效手段，势在必行。而海啸预报系统的一项主要工作是开发较为有效的海啸预报模型。

1 海啸预报模型介绍

自1960年代以来，美国就启动了海啸研究计划，美国国家海洋和大气局（National Oceanic and Atmospheric Administration，NOAA）开始着手建立国际海啸预警系统。随后，太平洋沿岸的北美、亚洲、南美的一些国家和地区也先后加入［2］。如今很多模型已经投入使用，其中几个典型的应用包括：NOAA海啸研究中心（NCTR）所应用的 MOST （Method of Splitting Tsunami）模型，日本东北大学研制的TUNAMI系列预报模型，美国康奈尔大学的COMCOT模型及特拉华大学的FUNWAVE／GEOWAVE模型，中国国家海洋环境预报中心开发的CTSU海啸数值模型等。

本文将分别从地震海啸波模拟的3个阶段——海啸的产生、传播和近岸海水的爬升，对以上几种数值模型进行对比和总结，希望能为海啸预报的进一步研究提供参考。

1.1 海啸波产生阶段的模拟

海啸波产生阶段模拟的主要任务是对由地震触发的海底变形所引起海表面初始扰动的准确估计。因此，海啸波产生模型的建立与地震震源机制的研究密切相关。

对于由地震触发的海啸，断层破裂能量迅速释放，其产生过程往往在很短的时间内完成。海啸模拟通常对流体域和固体域做解耦处理，采用瞬时变形的假设，利用地震弹性变形或粘弹性变形模型产生的形变作为初始波动场［3］。这样的近似做法是有理论分析依据的，结果也比较令人满意［3］。

美国NOAA目前主要使用MOST模型作为早期海啸监测和预报的一部分［4］。它是由南加利福尼亚大学研制的整套数值代码，其海啸产生模型以地震源的不平整平面模型为基础，将地壳与海水假定为弹性半空间上方的不可压缩流体层，并利用静态海底变形公式为接下来的海啸传播和增水提供初始条件。

由日本东北大学研制的TUNAMI模型是将海底地形数据和变形数据作为输入文件，利用软件FAULTWAVE.F进行计算，得出对应于水深数据的网格点处的海表面高度，作为初始波，为TUNAMI模型提供初始条件，即计算地震发生所产生的初始海表面高度。

由美国康奈尔大学土木工程系研究开发的COMCOT模型，专门模拟海水受到扰动后向外传播的过程，适用于长波运动，可用于海啸波引起的海洋沿岸灾害及工程的评估。在COMCOT模型中，海表面的初始变动是通过海底位移的计算产生的，计算的前提是海水不可压缩，海底为刚性，一旦海底产生错动，海面在垂直方向上瞬间产生位移，其值与海底位移相等［5］。且该模式中可使用2种塌陷模式：一种是弹性半空间断层模式［6］，另一种是基于 Okada［7］理论的模型，以计算海底垂向位移量，即初始海面垂向位移。

通过分析可见，以上海啸预报模型产生阶段的理论依据大体相同，利用地震震源机制得出海底位移，再根据假定水面的升降与海底的变化相同，得到海面水位变化值，为下一阶段的传播模型提供初始条件，中国的地震海啸数值模型等其他海啸预报模型大多以此依据获得初始条件。

1.2 海啸波的传播模型

海啸波产生后将会发展为重力长波向周围传播。在海啸抵达距离海啸源几百甚至几千公里的海岸之前，可以传播很长的距离，但其能量衰减却较少。所以海啸的传播具有大尺度特征，需要将地球的曲率、科氏力、频散等因素考虑在内。

MOST传播模型为精确模拟海啸远距离的传播，考虑了以上因素。在球坐标内引入科氏项，使用数值离散理论及分裂法求解非线性浅水波方程组的数值解［4］。

TUNAMI模型的基本原理与MOST传播模型类似，以非线性浅水方程为原始方程，采用有限差分法，但是TUNAMI模型考虑了底摩擦的影响。根据不同的应用和复杂程度，开发了不同的模型源代码，其中，TUNAMI－N1为研究局地海啸的数值分析模型，使用固定网格的线性理论；TUNAMI－N2模型在深海使用线性理论，浅海及陆地水位爬升采用浅水理论，网格为固定网格；而TUNAMI－N3模型为变网格的线性理论；在TUNAMI－F1模型中海啸的传播运用球坐标系下线性理论；TUNAMI－F2模型，则令海啸在大洋及近岸的传播采用线性理论［8］。TUNAMI模型在原始方程的基础上，根据不同的研究需要，改变坐标系及网格特征，做到模拟不同条件下海啸的传播过程。

TUNAMI模型的基本方程［8］，是将原始质量守恒方程和动量方程沿深度方向积分后得出的一个正压二维模型，它考虑底部摩擦，除了在陆地的爬升过程，传播过程中忽略水平涡度湍流。

TUNAMI模型在近岸非线性系统中采用带有摩擦项的浅水波方程组，海水通量和水面高度作为待求未知量［8］。与 MOST传播模型相比，TUNAMI模型适用范围更加广泛，即能够根据基本方程，按照研究需要将方程组进行变换，例如在大洋远距离传播时加入科氏力项等，改变坐标系及网格特征，这样分别得到TUNAMI模型的5种数学模型，方便易行，节约计算时间，模型的设置与海洋实际情况也更加符合，并且此传播模型可以计算出近岸水位的爬升。

与以上2个模型不同的是COMCOT模型模拟远距离及在深海传播的海啸时，使用线性浅水方程，即忽略非线性对流项、海底的摩擦项，当进行大尺度的海啸模拟时，考虑到了球坐标系的选取及科氏力的存在。球坐标系下，其控制方程为［5］：

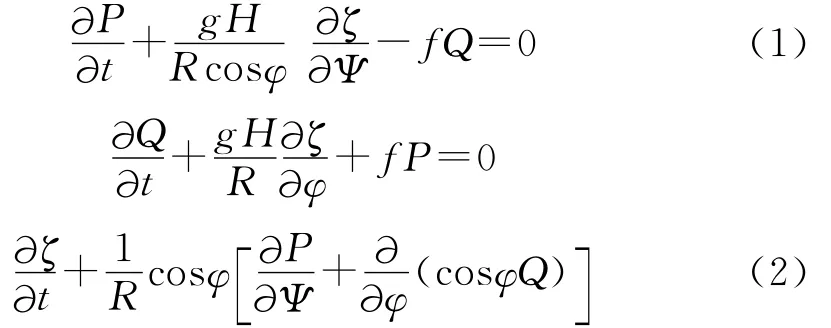
其中：ζ为波高；P，Q 分别为x，y方向的体积通量；u，v为x，y（或是经度及纬度）方向速度的垂向平均值；H是海水的总的深度（H＝ζ＋h）；h是海水的深度；g为重力加速度；R为地球半径；ψ，φ为经纬度；f是科氏参数［5］。

COMCOT模型中以交错式显性蛙跳式差分方法求解线性浅水方程，并利用蛙跳法的数值离散所产生的数值频散来仿效物理频散，解决了浅水区域的频散效应问题，使计算快速方便。

但是当海啸波传播到近岸时，水深变浅，海啸波波长变短，速度减慢，波高增大，这时非线性对流项及底部摩擦对海水的传播影响增大，又因为近岸海啸模拟的区域范围较小，因此在非线性浅水方程中纬度上的变化及科氏力的影响可以忽略［5］。此种情况下，COMCOT模型控制方程与TUNAMI模型的基本方程相同。

COMCOT模型与MOST模型的基本原理大致相同，其控制方程又与TUNAMI模型的相似，均是以海水的体积通量及海面波高作为待求未知量，且考虑了底摩擦的影响。

该模型的另1个特点是采用多层嵌套网格系统［5］，以节约计算资源和时间。采用多层嵌套网格系统的另1个原因是，随着计算区域的水深变化，需要使用不同的网格分辨率及时间间隔，以确保数值方法能适当的表示频散效应［5］。在COMCOT模型中不同的网格可选用不同的浅水方程，不同的坐标系，以及不同比例大小的地形网格资料，但彼此间又是相互影响，相互连接，能够保证模式计算的快速性及准确性，相对于MOST、TUNAMI模型来说，这是1个很大的优点。

中国的CTSU海啸数值模型使用Okada海啸源模型，传播模型内含球面坐标下的2种模型，1种为越洋海啸传播模型，1种是近海海啸传播模型［9］。其模型的控制方程与COMCOT模型基本一致，但求解方法略有不同。网格则采用多重双向嵌套网格［9］。这种双向嵌套网格计算方法，即为粗细网格相互影响的方法，这种方法不但可以较好地消除嵌套边界附近的寄生波，使计算稳定，而且可以较准确的刻画出当海啸波传播到岸边时细网格的解对粗网格的反馈作用，使粗网格的计算更加准确，从而使整个计算更逼近真实［9］。但是双向嵌套网格方法必须粗、细网格同时计算，计算量较大，为使模型能够快速计算，其并行版本已被开发。

与前几个模型不同的是James Kirby所开发的FUNWAVE模型，采用一维、二维2种形式的Boussinesq方程作为控制方程。由于Boussinesq方程的弱非线性及频散效应，更适合模拟海啸波动的传播过程［10］，FUNWAVE采用 Wei et al.［11］提出的完全非线性频散方程（详见文献［12］），并在其中引入波产生、摩擦阻尼、边界吸收、波破碎、移动海岸等附加项来模拟波浪和流的相互影响，为包含上述的几种影响，该模式将方程进行了扩展（详见文献［12］）。扩展后的Boussinesq方程可以根据需要改写成为Nwogu［13］扩展的Boussinesq方 程、Peregrine［14］的 标 准 Boussinesq 方程、非线性浅水方程等。为了模拟出浅水处拍岸浪的动力过程，带有涡度粘性的动力混合项加入方程中，模拟由于波浪破碎引起的能量耗散［10］。

可见，FUNWAVE模型中，使用了较复杂的Boussinesq方程，并将其扩展，从而使方程可以在改变控制参数的情况下，得到不同的控制方程，以适用于不同的研究目的和研究区域，适用范围很广泛。

而基于FUNWAVE，由Philip Watts开发的GEOWAVE模型，可用来模拟海啸的传播和上岸，并使用TOPICS模型来模拟滑坡引起海啸的初始波［10］。

从以上几个正投入使用的海啸传播模型可以看出，在浅水区域里，需要考虑波的频散效应，使用Boussinesq方程来计算较为适合，但是Boussinesq方程中的多阶项难以用数值方法求解，且需要较高的时空分辨率，为使计算能够方便快速，海啸传播模式是以浅水波动方程计算为主，并使用差分法的数值离散仿效物理频散，以解决波的频散效应。此外，完全非线性势流理论及Navier－Stokes方程也应用于海啸的模拟，然而对于实时模拟和重现海啸场景的模型［15］以上文所述的两类方程为主。

1.3 海啸预报模型的水位爬升模拟

海啸向陆地的爬升过程，由于非线性的增强、检测模型的高质量实地测量数据和较高分辨率的地形数据的缺乏，成为任何1个海啸模型最不成熟的一部分。

MOST模型的海水爬升过程由VTCS模型利用可变网格有限差分法来模拟，可获得最大波高、最大流速的空间分布、最大增水线以及可显示波到达后不同位置波高的时间序列。该模型利用以上2种高质量数据建立增水图，并根据未来有效数据的获得和沿海岸线的变化进行不断的维护和升级，而且实际模拟中MOST的增水模型得到了满意的结果。

TUNAMI海啸传播模型加入水平涡度湍流后，可以计算出水位的爬升，并且Yalciner在对2004年12月26日印度洋海啸的实地考察报告中，对观测数据与TUNAMI－N2模型的模拟结果做了比较，得到了较好的结果［16］。

FUNWAVE在改变扩展方程的参数后，可模拟出渗透性海底或狭槽性质的海岸水位爬升。而其他海啸爬升模型大部分是通过增加传播方程的非线性及加入底摩擦实现的。

1.4 其它海啸数值模型

除以上几种海啸数值模型以外，其它研究也为海啸的数值模拟做出很大贡献。例如由Randall Leveque等所开发的CLAWPACK是1个高分辨率模拟波动传播的有限体积法软件包，David George将其引入到海啸波的模拟中，并嵌入了由Marsha Berger所开发的自适应网格加密来捕捉更精细的波动信息［10］，建立了TsunamiClaw海啸模型。它以浅水波方程的保守积分形式作为控制方程，以一阶精度的Godunov方法对方程进行离散求解，洋底地形信息在方程中以产生源项的形式体现［10］。自适应网格加密有限体积法特别适合于求解保守系统，并允许在系统中存在不连续量，这使它能够从根本上捕捉到波分裂等细节［10］。并且Randall和David用CLAWPACK对一维斜坡上的波动传播问题及日本Monai地区的二维海啸上岸做了模拟，结果和解析解及实验室模拟结果吻合较好［10］；由美国康奈尔大学开发的基于高阶深度积分波动模型（aka Boussinesq模型）的中长波模型包CULWAVE也用来进行非线性弱频散的海啸模拟，并模拟了1998年的巴布亚岛新几内亚海啸，模拟结果与实测数据吻合的较好［17］；另 外 由 European Commission Joint Research Center提供的JRC模型，基于简单的重力驱动浅水波的速度近似随时间积分得到传播距离S＝初始波以震源中心或断层中心为中心点做点源触发，地形数据采用ETOPO5。虽然JRC模型不能得到波高信息，却可以根据给定地震的震级及发生地点的经纬度很快计算出波的到达时间（约15s），并发出初步警报［10］。

张超凡等用2种通用软件FEPG和PETSc开发的海啸模式，取得了较好的效果［10］。其中FEPG采用有限单元法求解非线性浅水波方程，PETSc采用有限差分法求解，2种模型的结果吻合很好，并同TUNAMI模型进行了比较，在均一地形下，结果吻合较好，但是对于实际复杂地形，传播图及波高出现较大差异，所以这种新的模型值得进一步研究［［18］。

而在2004年印度洋海啸大地震之后，德国政府要求以波茨坦地质研究中心（GFZ，德国国家地球科学实验室）为代表的亥姆霍兹国家研究中心联合会（Helmholtz）建立德国－印度尼西亚印度洋海啸早期预警系统（GITEWS）［19］。GFZ对所有现行数据的利用和分析第一次在极短的时间尺度内实现了受影响地区海啸淹溢的精确预测。由阿尔弗雷德－韦格纳研究所（AWI）开发的以非结构化三角网格计算为基础的新海啸模拟软件TsunAWI和GFZ对地壳变形／运动的模拟是实现这些预测的基础［19］。

此外还有不少的海啸预报模型及研究方法正在开发中，相信海啸的预警系统将会在未来的研究中更加准确、有效。

2 目前海啸模型需要克服的问题

现今海啸数值模型已有了很大的进展。一些海啸数值模型已用于实际的海啸预报工作，并可以基本模拟出海啸的产生及传播过程，但是由于海啸模拟的过程中，存在着数据不足和原理的假设等因素，成为现今海啸数值模型研究中需要解决的主要问题。

（1）大部分海啸是由海底地震引起的，海啸的数值模拟需要地震参数作为模拟的初始条件。所以在地震断裂带的海底和近海可能发生海啸的地带布设海底压力记录仪（BPR）阵列，与GPS系统、岸边和岛屿潮位站形成多层次的海啸监测网［20］，才能获得有效的地震数据，从而为海啸预报初始条件的生成提供数据。

（2）有效精确的海啸产生模型是准确模拟海啸传播的基础。现在使用的海啸产生模型由震源机制解推算海面初始波动状态，是通过瞬时变形假设，这显然与实际不符，因为地震发生后产生的余震等也会给海啸的产生与传播带来影响，为解决这一问题，研究者将地震产生的海底变形划分成不同区域，并分时间段加入至传播模型中，以模拟出较符合实际的海啸，但这需要精确的地震数据；而一些研究者开始了海啸生成的非线性机制的研究，如：Nosov等［21］研究了定常假设下在某一水层由高频底部振荡生成的长重力表面波的非线性机制，并得到了表面波振幅与底部振荡参数以及源区长度之间的关系［15］。Tony Song等利用沿海GPS系统研究，并且基于多个海啸地震数据和海洋数值模型模拟结果，证明不仅断裂地壳的垂直运动可对海啸起作用，断裂陆坡的水平运动通过向海洋传输动能也可增加海啸能［22］，并且断裂地壳的水平运动对海啸源起着重要的作用［23］。因此海啸产生的模拟不仅需要足够的地震监测数据，还需要正确的震源机制解及海底变形与其引起的初始海表面水位的关系，是海啸数值预报模型能够精确模拟海啸的必要前提。

（3）现在使用的海啸数值模型处于二维模拟的状态，以压强分布呈静水力学特性，垂向水平速度均匀为假设，不能用到结构物附近的海啸特性研究或水深变化剧烈的地方，在工程防御上受到了限制。为此，Masamura et al.首先开发了“非静水压强分布的三维模型”，模型里考虑了完全非线性和完全色散的影响［24］，但由于模型需要在水平方向、垂直方向进行分区交错计算，具有耗时、耗内存的缺点，这也是目前人们关注计算机并行计算的1个重要原因。因此，为克服以上难题，在模拟海啸作用于结构物的过程中，必须考虑湍流模型［24］。另外，潮汐对海啸在近岸的传播影响较大，如果在海啸模型中考虑到潮汐的影响，会使海啸的模拟更接近实际，也更能准确的反映潮汐影响下海啸的强度。

（4）海啸的预警需要估算海水传至近岸后水位爬升值，由于非线性的增强，这是海啸模拟最不成熟的部分，主要原因是2种数据的缺乏：监测模型的高质量实地测量和分辨率较好的海底地形数据。前1种数据可以近似的通过一些大规模试验获得，但须花费很大的人力物力。而通常海底地形数据的获取是采用ETOPO2数据，在近岸处非线性效应强烈，需要在更加精密的网格上计算，但这样的精细资料往往只在部分地区存在，因此，现今NOAA正在利用卫星对海底地形数据进行精确的收集［15］，为海啸近岸传播的精确模拟提供高分辨率的海底地形数据。

（5）为验证海啸预报模型的准确性，卫星测高技术提供的海面高度及海面梯度异常现象为海啸模拟的验证提供了依据。因此，在研究海啸数值预报模型的同时，海啸的观测技术应同步进行，充分利用卫星遥感、地面监测站及海面浮标系统的监测能力，尽可能的收集海啸数据，为海啸的模拟与预报提供有力的依据。

3 研究展望

（1）海啸在近岸水位陡增造成的危害与潮汐系统有重要的关系，潮汐的存在会使海啸传至近岸的水位评估出现高估或低估问题，当海啸传至近岸时，若此时为高潮，则海啸评估会出现低估的可能，反之亦然。因此在海啸模型中，充分考虑潮汐的作用对近岸的海啸水位评估准确性至关重要。而以上所提到的海啸数值预报模型多是基于简单的二维水动力方程，没有考虑潮汐作用，因此今后需要充分结合地质学与海洋学，将地震引发的海面水位抬升或下降作为初始条件，加入到海洋数值模型中，在潮汐模拟的基础上，模拟海啸的传播，进而进行地震多发地带沿岸海啸的评估，建立较为完善的海啸数值预报及预警系统。

（2）未来工作中将采用无结构网格全球海洋数值模型［25］（GOCTM）进行海啸波传播的模拟，该模型是在POM（Princeton Ocean Model）和 FVCOM （Finite Volume Coastal Ocean Model）海洋模式基础上，发展和建立的全球海洋与中国近海相互作用的模型，不仅具有一般海洋数值模型良好的水动力模拟能力，而且采用无结构三角形网格，具有局部网格加密的优点，可以根据研究目的加密所关心区域，相对于多层嵌套网格系统，在模型计算过程中，也节约了不同网格之间数据传递所需要的机时。另一个优点是采用全球范围的数值模拟，摆脱模型结果对开边界条件的依赖，可以得到较为精确的模拟结果。

（3）GOCTM模型中具有天体引潮力计算模块，该模块内引潮力的计算可与实际日期相对应，于是可以模拟出潮汐影响下某一时刻水位、流场分布，将该水位与海啸源初始水位场线性相加作为初始水位场，该时刻的流场作为初始流场，在打开潮汐模块的情况下，可以进行潮汐作用下，海啸波传播的模拟实验。

4 结论

由于近年来频频发生的海底地震引发多次海啸，尤其是太平洋地震带属于高发区，所以海啸数值预报模型的开发与进一步发展成为世界关注的问题。以上是各国开发的海啸数值预报模型的介绍与对比，部分模型已经应用到实际预报当中，并得到了不错的效果。从这些模型可以看出：

（1）海啸的数值预报应该包括3部分：由于海底变形引发的海啸产生过程，海底变形引起的海表面波动导致的海啸传播过程，海啸传至近岸的水位陡增过程。海啸产生过程需要地震数据的支持，以及精确的震源机制解；传播过程可以通过波动方程的数值解求得，验证则需要海面测高技术提供观测数据；而海水爬升过程则是通过强非线性方程进行模拟，但需要高分辨率的地形数据，这是海啸数值模拟中最不成熟的部分，也是现阶段国际上研究的重点。

（2）海啸的数值模拟大都为二维模拟，随着计算机性能的提高和数值计算方法的发展，海啸的三维模拟已经成为可能，为获得更为详尽的海啸物理过程信息，三维的海啸数值模拟成为海啸模拟的必然趋势。海洋数值模型的引入可以顺应此趋势，使海啸的的数值预报研究进入新的领域。

（3）本文作者下一步工作将是利用无结构全球海洋数值模型（GOCTM），在潮汐模拟的基础上进行海啸数值模拟及评估，希望可以在不久的将来建立完善的海啸数值预报及预警系统，有效减少海啸给我们带来的灾难。

［1］ 郭彩玲，王晓峰.中国东部海域发生海啸的可能性分析 ［J］.自然灾害学报，2007，16（1）：7－11.

［2］ 杨马陵.地震海啸监测预警现状与进展 ［J］.华南地震，2005，25（2）：22－29.

［3］ 赵曦，王本龙，刘桦.海沟内海底地震激发的表面波动 ［J］.力学季刊，2007，28（2）：195－200.

［4］ Titov V V，Gonzalez F I.Implementation and testing of the Method of Splitting Tsunami（MOST）Model［R］.［s.l.］：NOAA Technical Memorandum ERL PMEL－112，1997.

［5］ Liu P L F，Woo S B，Cho Y S.Computer programs for tsunami propagation and inundation［D］.US：Cornell University，1998.

［6］ Mansinha L，Smylie D E.The displacement fields of inclined faults［J］.Bulletin of the Seismological Society of America，1971，61（5）：1433－1440.

［7］ Okada Y.Surface deformation due to shear and tensile faults in a halfspace［J］.Bulletin of the Seismological Society of America，1985，75（4）：1135－1154.

［8］ Dr.Fumihiko Imamura，Dr.Ahmet Cevdet Yalciner.Res Assist Gulizar Ozyurt［R］.Tsunami Modelling Manual.http：∥www.tsunami.civil.tohoku，2006.

［9］ 于福江，叶琳，王喜年.1994年发生在台湾海峡的一次地震海啸的数值模拟 ［J］.海洋学报，2001，23（6）：32－39.

［10］ 张超凡，石耀霖.海啸灾害的数值模拟研究 ［J］.中国科学院研究生院学报，2008，25（3）：292－295.

［11］ Wei G，Kirby J T，Grilli S T，et al.A fully nonlinear Boussinesq model for surface waves［J］.Journal of Fluid Mechanics，1995，294：71－92.

［12］ Kirby J T，Wei G，Chen Q，et al.FUNWAVE 1.0：fully nonlinear boussinesq wave model documentation and user's manua1［R］.Research Report.No.CACR－98－06.Center for Applied Coastal Research，University of Delaware.http：∥chinacat.coasta1.ude1.edu／～kirby／pregrams／nearcom／documentation.Html，1998.

［13］ Nwogu O.An alternative form of Boussinesq equations for near－shore wave propagation ［J］.J Waterway Port Coast Ocean Eng ASCE，1993，119（6）：618－638.

［14］ Peregrine D H.Long wave on a beach［J］.J Fluid Mesh，1967，27：815－820.

［15］ 姚远，蔡树群，王盛安.海啸波数值模拟的研究现状 ［J］.海洋科学进展，2007，25（4）：487－494.

［16］ Yaleiner A C，Perineek D，Ersoy S，et al.December 26，2004 Indian Ocean tsunami field survey （Jan.21～31，2005）at North of Sumatra Island［R］.UNESCO IOC Report，2005.http：∥yaleiner.ce.metu.edu.tr／sumatra／survey／yaleiner－et－al－2005.Pdf.

［17］ Kim Roddis W M.Community Workshop on Computational Simulation and Visualization Environment for the Network for Earthquake Engineering Simulation （NEES）［R］.Lawrence，KS：Sponsored by the National Science Foundation（NSF）.2003：15.

［18］ 张超凡，石耀霖.利用PETSc和FEPG编制海啸数值模拟程序的研究 ［J］.地震，2008，28（1）：47－56.

［19］ 赵纪东.印度洋海啸早期预警系统的现状 ［J］.科学研究动态监测快报，2008，5：7－10.

［20］ 叶琳，于福江，吴玮.我国海啸灾害及预警现状与建议 ［J］.海洋预报，2005，22（S1）：147－157.

［21］ NOSOV M A，Skachko S N.Nonlinear tsunami generation mechanism ［J］.Natural Hazards and Earth System Sciences，2001，1：251－253.

［22］ Alan Buis.NASA Demonstrates Tsunami Prediction System.http：∥www.jpl.nasa.gov／news／news.cfm？release＝2010－198.

［23］ Song Y T，Fu L L，Zlotnicki V，et al.The role of horizontal impulses of the faulting continental slope in generating the 26December 2004Tsunami［J］.Ocean Modelling，2008，4（20）：362－379.

［24］ 祝会兵，于颖，戴世强.海啸数值计算研究进展 ［J］.水动力学研究与进展，2006，21（6）：714－723.

［25］ 于华明.基于可变网格模型系统的全球海洋与中国近海潮汐研究 ［D］.青岛：中国海洋大学海洋环境学院，2008.