PA6／POE共混物的分子动力学与介观动力学模拟

张彦飞，兰艳花，付一政，赵贵哲，胡国胜

（1中北大学 山西省高分子复合材料工程技术研究中心，太原030051；2中北大学 材料科学与工程学院，太原030051；3北京理工大学材料科学与工程学院，北京100081）

尼龙6（PA6）因具有很好的机械强度和刚度而被广泛应用于结构部件，由于具有很好的耐磨损特性，还用于制造轴承。为了提高PA6的抗冲击性在其中加入合成橡胶，如三元乙丙橡胶（EPDM）和丁苯橡胶（SBR）等。而聚烯烃弹性体（POE）分子结构与EPDM相似，也具有耐老化、耐臭氧、耐化学介质等优异性能，今后POE可能取代传统的EPDM和SBR。POE主要用于改性增韧PA，PP和PE在汽车工业方面制作保险杠、挡泥板、方向盘、垫板等，PA6与POE共混可以相互取长补短，获得所需要的使用性能［1－4］。通过传统的实验方法研制出性能优异的塑料聚合物配方，需耗费大量人力、物力和财力，且研制周期较长；加之某些材料均具有自身氧化和分解的特点，在一定温度以上会加速分解，配方实验具有一定的危险性。计算机多尺度模拟方法被定义为一种科学工程技术，它将模型、模拟现象以及复杂体系不同模拟尺度的结果结合起来计算分析结构复杂的材料，是一种经济、有效的方法。有效的跨尺度模拟方法可以求解从宏观到微观的问题，大尺度计算为小尺度计算的界面提供边界条件，从而使内部的多尺度描述表达清楚；小尺度计算所得的物理量通过一定的等效方法向大尺度传递，从而可以准确了解系统整体的物理化学特征。越来越多的学者利用分子动力学解决实际问题［5，6］，因此，本工作在配方设计的理论基础之上，应用分子动力学（MD）模拟对PA6与POE的相容性进行研究，预测共混物的玻璃化转变温度和其径向分布函数，观察共混物的相容性好坏，并对共混物的结合能以及力学性能进行预测。应用介观动力学（MesoDyn）模拟对PA6／POE共混物进行研究，通过其共混物等密度图、有序度参数以分析共混物相容性的好坏，并与微观相联系，通过理论计算分析其实验中的宏观性能。

1 模型构建与模拟方法

1.1 物理模型分子建模过程及模拟细节

模拟所用的POE为杜邦Dow弹性体公司，牌号Engage 8200，乙烯与1－辛烯共聚物，其中1－辛烯含量为24%，根据POE分子结构确定其x∶y＝13，基于简单与计算量的考虑，定义x＝13，y＝1，分子结构见图1。运用 Materials Studio（MS）软件包中Visualizer模块依据图1建立相应的PA6和POE的分子模型，所建立的PA6和POE的无定形分子模型如图2（a），（b）所示。通过Synthia模块中的QSPR方法求得PA6和POE的极限特征比C∞分别为6.06和7.62，故在混合物中PA6和POE分子分别包含6和8个重复单元，结合实验中PA6与POE的质量比为7∶3，每个共混物无定形分子模型中均包含一条POE分子链，相应的PA6分子个数为13，计算得共混物的初始密度为0.9678g·cm－3，所建立的 PA6／POE共混物的无定形分子模型如图2（c）所示，球棒模型代表PA6分子链，CPK模型代表POE分子链。

图1 PA6和POE的分子结构式Fig.1 Chemical structures of PA6and POE

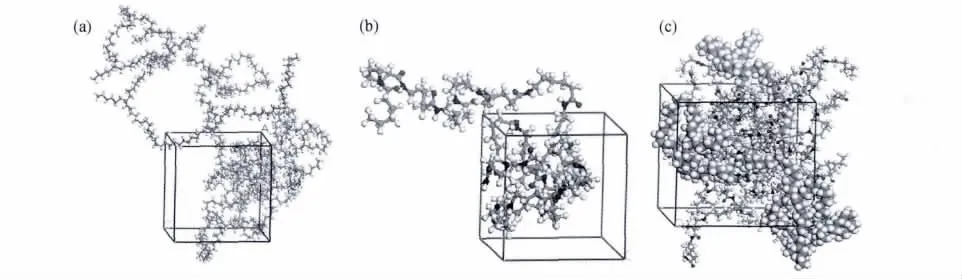
图2 PA6（a），POE（b）和PA6／POE（c）的无定形分子模型Fig.2 Snapshot of the amorphous unit cells for PA6（a），POE（b）and PA6／POE（c）blends

采用Smart Minimization方法对所构建的无定形分子模型进行结构优化，将经过优化的无定形分子模型进行退火处理，用来消除模型构建过程中产生的局部不合理结构。退火采用5个循环，温度梯度为50K，初始温度为300K，中间温度为600K。为了更快达到平衡，首先进行200ps的等温等容（NVT）系统的MD模拟，再进行100ps等温等压（NPT）系统的 MD模拟，每1000fs作为1帧保存，最后10帧用于分析性能。模拟过程中采用 Andersen［7］控温方法和Berendsen［8］控压方法，范德华作用力（vdw）采用 Atombased［9］法，静电作用力（Coulomb）采用 Ewald［10］法，非键截断半径为0.95nm，样条宽度（Spline Width）取0.1nm，缓冲宽度（Buffer Width）取0.05nm，时间步长1fs，力场选择COMPASS［11］。

1.2 介观建模过程及MesoDyn模拟细节

在介观动力学模拟中，为了表征体系的化学性质，需要确定两类重要参数：一类是表示各个重复单元的高斯链，另一类是不同珠子之间的相互作用参数。

1.2.1 珠子结构的选择

介观动力学模拟方法的思路是：均相态体系的自由能与区域密度函数之间有一定的函数关系，并且从自由能可以得出所有的热力学函数，进而研究共混体系的各种性质。在MesoDyn模拟之前，需要对体系进行粗粒化描述，即对珠子的划分以及确定各个重复单元的高斯链，原始体系的粗化程度影响着高斯链的拓扑结构。根据式（1）可以得出模拟分子的高斯链结构。

式中：NMes为高分子链粗粒化后所包含珠子的个数；N为聚合度；C∞为高分子链的极限特征比。通过MS软件Synthia模块中的QSPR方法求得POE和PA6的极限特征比C∞，从而得到聚合物的珠子个数，结果如表1。

表1 PA6和POE的介观参数Table 1 Mesoscopic parameters of PA6and POE

1.2.2 Flory－Huggins（χ）相互作用参数

Flory－Huggins相互作用参数（χ）是高分子物理中最重要的物理参数之一。它反映高分子共混时相互作用能的变化，可作为判断混合物相容性好坏的一个判据，根据式（2）可以得到POE与PA的Flory－Huggins参数：

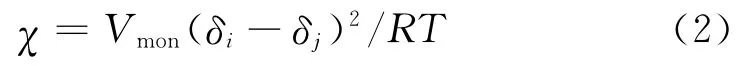
式中：χ为POE与PA的Flory－Huggins相互作用参数；Vmon为单体的摩尔体积；R为理想气体常数；δi，δj分别为POE和PA的溶度参数；摩尔体积Vmon和溶度参数δ均通过MS软件Synthia模块中的QSPR方法求得，一般δi－δj＞2.1为不相容体系。根据式2求得POE／PA6的Flory－Huggins参数，进而计算出 Mesodyn模拟中输入的相互作用参数值，详见表2。

表2 Mesodyn模拟参数Table 2 MesoDyn simulation parameters

1.2.3 其他介观模拟参数的选择

利用MS软件的MesoDyn模块，计算在尺寸为32nm×32nm×32nm的周期性边界条件的盒子中进行，设定PA6与POE的质量比为7∶3，所有珠子的扩散系数为1.0×10－7cm2·s－1，体系的噪音参数设Ω≡V－1h3＝75，温度为298K，可压缩参数设为10。考虑到体系的平衡时间将模拟步长设为Δτ＝20ns，模拟总步数为50000步，总的模拟时间为1000μs。

2 结果与讨论

2.1 POE／PA体系Tg预测

对于高分子材料二元共混物的Tg，许多研究者基于经验数据拟合、经典热力学等方法得到了大量的关于混合体系Tg与组成之间的关系式，这些关系表达式在一些体系中与实验结果符合很好，但是依然缺乏更普遍的理论来解释和预测在聚合物混合体系中的玻璃化转变现象。目前关于高分子的玻璃化转变机理，主要有如下3种理论：自由体积理论、热力学理论和动力学理论［12］。

本工作根据自由体积理论通过在一定范围（此温度范围包括其对应的由实验得到的Tg）内，由MD模拟所得到的比体积对温度作图，然后在实验报道的Tg之上和之下温度范围的数据点作线性拟合分别得到两条直线，这两条直线交点的横坐标即为Tg。共混物体系相容性的好坏可以通过共混物的玻璃化转变温度变化来表征；如果共混物体系完全相容，则只有1个Tg，处于两组分的Tg之间，并且随着组分含量不同，其玻璃化转变温度也会改变；如果体系完全不相容，则表现出多个与纯组分相对应的Tg。

如图3所示，通过分子模拟得到PA6／POE共混物有两个玻璃化转变温度，其中较低的温度为218.52K，对应于 POE的Tg（220.28K），而较高的温度为313.89K，对应于PA6的Tg（313～323K）［12］，对于PA6／POE共混体系，由于两者相容性不好，故在各自的纯物质的玻璃化转变温度附近出现拐点。虽然自由体积理论并不能完全解释玻璃化转变的机理，但用分子动力学模拟得到的体积－温度关系曲线来预测高分子的Tg还是比较可信的。

图3 PA6／POE的比体积与温度曲线关系Fig.3 The specific volume and temperature curves for PA6／POE

2.2 径向分布函数g（r）

分子间径向分布函数g（r）可以揭示非键原子间相互作用方式和本质，是反映材料微观结构的特征物理量，它表示在一个分子周围距离为r的地方出现另一个分子的概率密度相对于随机分布概率密度的比值。氢键作用范围为0.26～0.31nm，范德华力作用范围为0.31～0.50nm。

图4为PA6和POE纯物质的g（r），PA6与POE在r＜0.7nm时，峰值比较一致，r＞0.7nm则表现出PA6远离POE的情况，故PA6与POE近程结构相似，远程相差较大。一般来说，两种物质结构比较相似容易相容，即相似相容。为了更好地揭示共混物分子间相互作用本质，本工作分析了298K时PA6／POE共混物分子模型中分子间的g（r），由图5可见，共混物分子间主要作用方式为范德华作用力，共混物之间并不存在氢键的作用，分子间的结合力主要来自于范德华作用力。Mattice等认为如果共混物中同组分的分子间径向分布函数值比两组分分子间的径向分布函数值低，组分会发生相容，反之则会发生相分离［13，14］。由图5可见，共混物分子间主要作用方式也为范德华作用力，同时在PA6／POE共混物中PA6／POE和PA6－PA6的分子间径向分布函数值比较接近，而且远高于POE－POE分子间径向分布函数值，则可以判断体系相容性不好。

图4 PA6，POE纯物质的g（r）Fig.4 Intermolecular pair correlation function for PA6and POE

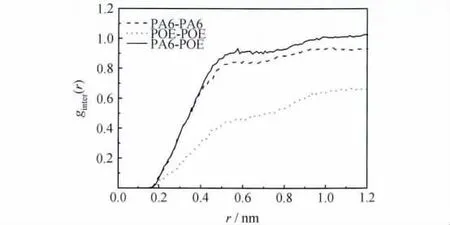
图5 PA6／POE共混物的g（r）Fig.5 Intermolecular pair correlation function for PA6／POE

2.3 PA6／POE体系力学性能的预测

原则上讲，材料的所有力学性质均可从它的弹性系数矩阵导出。由于弹性应变能的存在，极端各向异性体满足Cij＝Cji，即独立的弹性常数只有21个。对于各向同性体，仅有2个独立的弹性常数，故用两个拉梅系数即可求出各模量和泊松比［15］。本工作考察了298K时PA6与POE共混物的弹性系数矩阵，结果如表3所示（其余常数均趋近于零，没有列出）。

表3 PA6／POE的弹性系数（GPa）Table 3 Coefficient of elasticity of PA6／POE（GPa）

对于 PA6／POE共混物，C11、C22、C33组，C44、C55、C66组和C12、C13、C23组数值相差较大，反映PA6／POE的各向异性，导致体系在不同方向的物理化学特性也不同，各向异性具体表现在不同方向上的弹性模量、硬度、热膨胀系数、导热性等都是不同的，这对混合物的性能会产生大的影响。柯西压（C12－C44）表征了材料的脆性和韧性，一般柯西压大于0为韧性材料，柯西压越小，其韧性越弱，从表3中得到，PA6／POE的柯西压值为1.08，说明共混物具有较好的韧性。

一般橡胶的泊松比ν值为0.5，由表4可见，PA6中加入POE后，可以降低其刚性，增加柔性，其泊松比也随之会提高。体模量与剪切模量的比值即K／G，可用来衡量体系的韧性，这是材料由于塑性变形而吸收能量的性质，PA6／POE体系的K／G＝3.157，表明其韧性较好。

表4 PA6／POE的力学性能Table 4 Mechanical properties of PA6／POE

2.4 PA6／POE体系结合能的预测

相容性的本质是各组分的分子间相互作用，而共混物各组分间的相互作用直接影响其机械强度和相容等性能。寻找与基体材料结合能大的高分子和匹配好的助剂已成为塑料配方设计中的关键因素。

分子间相互作用能（ΔE）或分子间结合能（－ΔE）可定量地表征分子间相互作用的强度［16，17］。以稳定构型下各体系的总能量进行分子间相互作用能计算，PA6与POE的平均相互作用能（Einter）可表示为：

式中EPA6／POE为PA6／POE共混物的平均总能量，EPA6为POE／PA稳定结构去掉POE的平均单点能，EPOE为PA／POE稳定结构去掉PA6的平均单点能，通过式（3）可以得到PA6与POE的平均相互作用能。

定义结合能（Ebind）为相互作用能的负值，即Ebind＝－Einter。

若不考虑MS程序自行产生的能量校正值，通过比较各能量项对结合能的贡献，可以发现结合能在数值上近似等于非键能，即为范德华力和静电力之和，共混物体系中范德华力约占89.88%，静电力约占0.05%，剩余为限制力的作用，可见PA6与POE分子间相互作用的本质为非键能中的范德华作用能和静电能，范德华作用能所占比例较大，其次限制能也占很重要的作用，但键能（包括分子键能，键角能，二面角扭转能，离平面能，交叉能）对结合能并未能起到任何作用，结合能主要在于分子间的作用，一些原子分子水平的作用力对结合能的影响甚微。

表5 PA6与POE的结合能（kJ·mol－1）Table 5 Binding energy of PA6／POE（kJ·mol－1）

2.5 MesoDyn模拟结果分析

图6为PA6与POE共混物（PA6∶POE＝7∶3）的等密度图。模拟初始，PA6与POE均匀混合在一起；随着模拟时间的延长，POE相开始聚集，颗粒由小变大；随着模拟时间的继续增加，POE相继续聚集，最终形成较大颗粒分散相分散在PA6相中，说明该混合物相容性不好。

图6 PA6／POE共混物的等密度图 （a）0μs；（b）10μs；（c）20μs；（d）30μs；（e）200μs；（f）500μs；（g）1000μsFig.6 The isosurface of the density fields for PA6／POE（a）0μs；（b）10μs；（c）20μs；（d）30μs；（e）200μs；（f）500μs；（g）1000μs

由有序度参数图图7可以观察到：模拟初始，PA6的有序度参数急剧增加，当模拟时间增到100μs后，随着模拟时间的进一步延长，体系的有序度参数波动较小，达到平衡状态。由于共混物的有序度参数大于0.1，说明PA6与POE以7∶3形成的混合物是不相容的，与前面得出的结论一致。

3 结论

（1）分子动力学可以比较准确预测PA6／POE的玻璃化转变温度，且PA6与POE共混物为不相容体系。

图7 POE与PA6共混物（PA6∶POE＝7∶3）有序度参数Fig.7 The order parameter for PA6／POE（PA6∶POE＝7∶3）

（2）分析PA6和POE纯物质和共混物的分子间径向分布函数，纯PA6和POE及共混物各组分分子间主要作用方式为范德华作用力，通过比较共混物分子间径向分布函数可预测共混物的相容性。

（3）对PA6／POE共混体系的力学性能进行了预测，共混物拉伸模量、体积模量及剪切模量比较小，韧性比较好。

（4）介观动力学模拟中的等密度图与有序度参数说明PA6与POE相容性不好，与分子动力学模拟的结果一致。

［1］ BAI S L，WANG G T，HIVER J M，et al.Microstructures and mechanical properties of polypropylene／polyamide 6／polyetheleneoctene elastomer blends［J］.Polymer，2004，45（9）：3063－3071.

［2］ SELL C G，BAI S L，HIVER J M.Polypropylene／polyamide 6／polyethylene－octene elastomer blends［J］.Polymer，2004，45（17）：5785－5792.

［3］ MA L F，WEI X F，ZHANG Q.Toughening of polyamide 6with β－nucleated thermoplastic vulcanizates based on polypropylene／ethylene－propylene－diene rubber grafted with maleic anhydride blends［J］.Materials ＆ Design，2012，33（1）：104－110.

［4］ DAS A，MAHALING R N，STÖCKELHUBER K W，et al.Reinforcement and migration of nanoclay in polychloroprene／ethylene－propylene－diene－monomer rubber blends［J］.Composites Science and Technology，2011，71（3）：276－281.

［5］ 张兴丽，孙兆伟.基于分子动力学对超晶格结构界面热阻的模拟研究［J］.航空材料学报，2011，31（4）：7－10.ZHANG Xing－li，SUN Zhao－wei.Molecular dynamics simulation on thermal boundary resistance of superlattice structure［J］.Journal of Aeronautical Materials，2011，31（4）：7－10.

［6］ 王建伟，尚新春，吕国才.bcc－Fe空位浓度对辐照损伤影响的分子动力学模拟［J］.材料工程，2011，（10）：15－18.WANG Jian－wei，SHANG Xin－chun，LU Guo－cai.Molecular dynamics simulation of vacancy concentration on irradiation cascades damage effects in bcc－Fe［J］.Journal of Materials Engineering，2011，（10）：15－18.

［7］ ANDERSEN H C.Molecular dynamics simulations at constant pressure and／or temperature［J］.Journal of Chemical Physics，1980，72（4）：2384－1－10.

［8］ BERENDSEN H J C，POSTMA J P M，VAN GUNSTEREN W F，et al.Molecular dynamics with coupling to an external bath［J］.Journal of Chemical Physics，1984，81（8）：3684－1－7.

［9］ KARASAWA N，GODDARD W A.Force fields，structures，and properties of poly（vinylidene fluoride）crystals［J］.Macromolecules，1992，25（26）：7268－7281.

［10］ EWALD P P.Die berechnung optischer und elektrostatischer gitterpotentiale［J］.Annalen der Physik，1921，369（3）：253－287.

［11］ SUN H.Compass：an abinitio force－field optimized for condensed－phase applications overview with details on alkane and benzene compounds［J］.Journal of Physical Chemistry B，1998，102（38）：7338－7364.

［12］ 何曼君，张红东，陈维孝，等.高分子物理［M］.3版.上海：复旦大学出版社，2007.109－122.

［13］ CLANCY T H，PUETZ M，WEINHOLD J D，et al.Mixing of isotactic and syndiotactic polypropylenes in the melt［J］.Macromolecules，2000，33（25）：9452－9463.

［14］ AKTEN E D，MATTICE W L.Monte Carlo simulation of headto－head，tail－to－tail polypropylene and its mixing with polyethylene in the melt［J］.Macromolecules，2001，34（10）：3389－3395.

［15］ QIU L，XIAO H M.Molecular dynamics study of binding energies，mechanical properties，and detonation performances of bicyclo－HMX－based PBXs［J］.Journal of Hazardous Materials，2009，164（1）：329－336.

［16］ 肖继军，黄辉，肖鹤鸣.HMX晶体和HMX／F2311PBXs力学性能的 MD模拟研究［J］.化学学报，2007，65（17）：1746－1750.XIAO J J，HUANG H，XIAO H M.MD simulation study on the mechanical properties of HMX crystals and HMX／F2311PBXs［J］.Acta Chim Sinica，2007，65（17）：1746－1750.

［17］ TANAKA G，GOETTLER L A.Predicting the binding energy for nylon 6，6／clay nanocomposites by molecular modeling［J］.Polymer，2002，43（2）：541－543.