纤维取向对三维四向编织复合材料与层合复合材料振动性能的影响
裴晓园,李嘉禄,何玉强
(1天津工业大学 复合材料研究所 教育部先进纺织复合材料重点实验室,天津300160;2新天绿色能源(丰宁)有限公司,河北 丰宁068300)
与传统层合复合材料相比,三维编织复合材料可以直接织造出形状复杂、不同尺寸的整体编织预制件,从而实现制件的净尺寸制造,实现材料与构件的一体化、集成化设计制造,在航空、航天等领域得到了越来越广泛的应用[1-4]。模态是结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型[5]。结构的质量分布反映了体系在振动过程中的惯性分布;刚度特性反映了体系的弹性变形能力;阻尼反映了体系在振动过程中能量耗散性能。
研究复合材料的模态性能是认清复合材料在不同振动和噪声环境下的可靠性、保证结构安全服役的重要基础。现在,对复合材料振动特性的研究逐渐得到了人们的重视。Schultz和 Tsai[6]、Hashin[7]、Adams等[8-10]进行了复合材料阻尼的开创性研究工作;E.C.Botelho等在自由振动模式下对连续纤维/金属复合材料的模态阻尼行为进行了研究[11];武海鹏等用悬臂梁法对玻璃纤维和炭纤维复合材料进行阻尼测试;并用Adams-Bacon法和Ni-Adams法对实验结果进行了分析[12]。在三维编织复合材料方面,卢子兴等分析了玻璃纤维三维编织复合材料悬臂梁的振动特性[13];李典森等进行了玻璃纤维三维编织复合材料振动阻尼特性的实验研究[14]。本工作对炭纤维三维四向编织复合材料进行了悬臂梁模态实验测试,研究了编织角对三维四向编织复合材料的模态参数(损耗因子、固有频率)的影响;同时,研究了不同铺层角度的炭纤维层合复合材料的动态特性,并且对这两种复合材料的振动性能进行了比较。
1 炭纤维三维四向编织复合材料和层合复合材料的制备
实验采用密度 1.76g/cm3,线密度0.8g/m 的T700-12K炭纤维制作三维四向编织复合材料试件。图1给出了三维四向编织复合材料的内部结构图,图2给出了三维四向编织复合材料的表面结构图。图1中γ是内部编织角,图2中α是表面编织角。图3是实验用三维四向编织复合材料试件。内部编织角γ和表面编织角α之间的关系见公式(1):


图1 三维四向编织复合材料内部结构Fig.1 Inner structure of 3-dimension and 4-direction braided composites
为了与层合复合材料的动态特性相比较,对相同尺寸的层合复合材料试件也进行了实验模态分析。图4中的层合复合材料采用面密度为500g/m2的T700-12K炭纤维平纹布铺制成。在层合复合材料中,平纹织物的经纱方向和试样的长度方向之间的角度定义为纤维取向角。层合复合材料的取向角分别是30°,40°,45°。
所有试件的固化均采用树脂传递模塑法简称RTM (Resin Transfer Molding)工艺,制成复合材料试件。

用于模态实验用的复合材料试件尺寸的平均值,长:250mm,宽:25mm,厚:4mm。
用于模态测试的3组(每组3个试件)三维四向编织复合材料试件的相关参数(3个试件的平均值)列于表1。用于模态测试的3组(每组3个试件)层合复合材料试件的相关参数(三个试件的平均值)列于表2。
从表1和表2中可以看到,这两种复合材料的纤维体积分数比较接近,在52.27%~54.8%的范围内;纤维取向角度基本一致,但三维四向编织复合材料的内部编织角表示的是纤维在空间的取向,表面编织角表示的是纤维在平面的取向;通过测量三维编织复合材料的表面编织角,计算出三维编织复合材料的内部编织角。层合复合材料的纤维取向角度表示的是纤维的平面取向。在三维编织复合材料结构中,内部纤维成空间取向,而在层合复合材料结构中的纤维无空间取向,所以本工作中对比的是三维编织复合材料的空间纤维取向角度(即:内部编织角)与层合复合材料的平面纤维取向角度对其模态性能的影响。

表1 三维四向编织复合材料模态实验件的规格(平均值)Table 1 Specifications of mode experiment samples of 3-dimension and 4-direction braided composites(average value)

表2 层合复合材料模态实验件的规格(平均值)Table 2 Specifications of mode experiment samples of laminated composites(average value)
2 实验装置
图5为复合材料悬臂梁振动模态的实验系统的模拟图。实验中,试件一端被固支,呈悬臂状态,使用单入单出(SISO)识别法锤击悬臂梁的“根部”(距离夹持点约2cm处)。图6是装有力传感器的手锤对被测对象施加一个局部的激励,由通道1采样得到的力的脉冲信号;在实验中引入力窗函数,是为了在进行信号采样及数据处理时,尽量减小干扰信号的引入以及控制力锤敲击力的大小和采样时间。用加速度传感器从被测试对象得到测点的加速度响应信号,与冲击力信号一起经过A/D转换器及FFT分析仪进行传递函数估计,并由模态分析系统提供模态参数。
3 结果与讨论
根据振动衰减波形,通过公式(2),(3)可以得到悬臂梁振动的阻尼Δ和阻尼比η[11,15]。


式中:η为悬臂梁的振动阻尼比;Χn,Χn+1分别为衰减曲线中相邻两个振幅曲线的峰值。
在自由振动下,悬臂梁振幅的时程信号通过进行快速傅里叶转换(FFT),便可得到悬臂梁的振动频谱图[16]。
根据公式(4)可以获得225mm长,25mm宽,4mm厚的长方体悬臂梁试件的存储模量[8]。

E′是弹性模量(GPa);f是固有频率(Hz);I是惯性矩(m4);M是加速度计的质量(kg);m是试件的质量(kg);L是试件的长度(m)。
损耗因子tanx可以从下面的振动衰减波形中通过公式(5)计算得到。

损耗模量E″可以通过公式(6)获得:

三维四向编织复合材料模态实验的结果见表3,层合复合材料模态实验的结果见表4。

表3 三维四向编织复合材料前三阶模态参数(平均值)Table 3 First three modal factors of 3-dimension and 4-direction braided composites(average value)
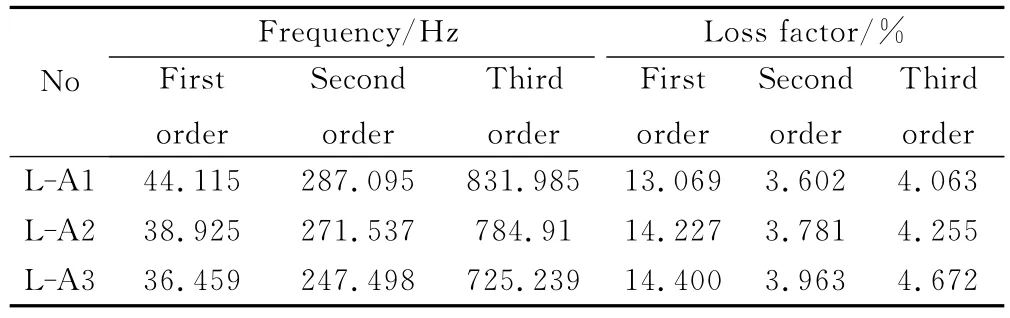
表4 层合复合材料前三阶模态参数(平均值)Table 4 First three modal factors of laminated composites(average value)
3.1 纤维取向角度对复合材料固有频率和阻尼比的影响
图7是三维四向编织复合材料和层合复合材料的纤维取向角度与固有频率间的关系图,从图7可知,当纤维体积含量相同时,曲线的变化规律基本一致,即三维四向编织复合材料与层合复合材料的固有频率随着纤维取向角度的增加而减小。
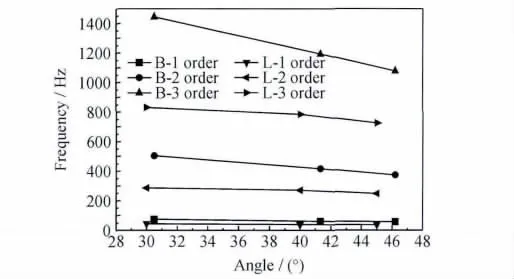
图7 三维四向编织复合材料与层合复合材料固有频率随纤维取向角度变化曲线图Fig.7 Natural frequency curve of composites with different fiber orientation angle
根据公式(4)可知当梁的外部尺寸相同时,固有频率的大小主要取决于材料的弹性模量。因此,三维四向编织复合材料与层合复合材料梁的固有频率随细观结构参数的变化可归因为细观结构参数对材料弹性模量的影响。由图1的三维编织复合材料内部结构图可知,三维四向编织结构内部编织纱的走向随着表面编织角的减小而变得更加平直,增大了轴向强度,沿四向纱方向的弹性模量也随之增大,使得三维四向编织复合材料固有频率增大。
从图7中可知,在纤维取向角度基本相同的情况下,层合复合材料的固有频率均小于同阶次的编织复合材料,例如:内部编织角为30.06°的三维四向编织复合材料的一阶固有频率要比纤维取向角为30°的层合复合材料的一阶固有频率高58.68%;二阶固有频率高75.61%;三阶固有频率高73.79%。内部编织角为43.31°的三维四向编织复合材料的一阶固有频率要比纤维取向角为40°的层合复合材料的一阶固有频率高54.95%;内部编制角为46.20°的三维四向编织复合材料的一阶固有频率要比纤维取向角为45°的层合复合材料的一阶固有频率高57.88%。这是因为三维编织结构是具有多轴纤维取向的高度整体化的连续纤维集合体。而传统的层合板复合材料与三维编织结构相比具有难以克服的固有缺陷,比如:沿厚度方向的刚度和强度性能较差,面内剪切和层间剪切强度较低,易分层,并且冲击韧性和损伤容限水平都较低。综上所述,这都使得在纤维取向角度基本相同的情况下,三维编织复合材料的固有频率要高于同阶次的层合复合材料的固有频率。
复合材料的损耗因子还可以通过材料的比阻尼容量计算求得。根据材料和结构比阻尼容量(SDC)定义公式(7)[14]:

式中:ΔU表示一个交变应力周期内材料和结构的耗散能量;U表示一个交变应力周期内材料和结构的最大应变能量。
图8是三维四向编织复合材料和层合复合材料的纤维取向角度与损耗因子间的关系图。从图8分析可知,纤维取向角度越大,材料的损耗因子越大。相同纤维取向角度的情况下,三维四向编织复合材料的一阶、二阶损耗因子均小于层合复合材料。随纤维取向角度的增大,相同纤维取向角度的三维编织复合材料的三阶损耗因子与层合复合材料的三阶损耗因子间的差距越来越小,甚至大于层合复合材料的损耗因子。例如:内部编织角为30.06°的B-A1三维四向编织复合材料的一阶损耗因子(8.340%)比纤维取向角为30°的LA1层合复合材料一阶损耗因子(13.069%)低36.18%;二阶损耗因子(2.531%)要比层合复合材料的二阶损耗因子(3.602%)低29.7%;三阶损耗因子(4.057%)要比层合复合材料的三阶损耗因子(4.063%)低0.001%。内部编织角为46.20°的4-B-A3三维四向编织复合材料的一阶损耗因子(9.313%)比纤维取向角为45°的L-A3层合复合材料一阶损耗因子(14.400%)低35.33%;二阶损耗因子(3.234%)要比层合复合材料的二阶损耗因子(3.963%)低18.4%;但是三阶损耗因子(4.842%)要比层合复合材料的三阶损耗因子(4.672%)高3.645%。这说明,随着纤维取向角度的增加,在纤维取向角度基本相同的情况下,三维编织复合材料前三阶的损耗因子和层合复合材料的损耗因子的差距在减小。并且,在纤维取向角比较大的情况下,三维四向编织复合材料的三阶损耗因子要大于层合复合材料的同阶损耗因子。因此,三维四向编织复合材料的减振性能与层合复合材料相比,虽然在低阶阻尼性能方面并不占优势,但是在高价阻尼性能方面不比层合复合材料差,甚至比层合复合材料要好。
图8 三维四向编织复合材料和层合复合材料的损耗因子随纤维取向角变化曲线图Fig.8 Loss factor of composites with different fiber orientation angle
在纤维取向角度基本相同的情况下,三维编织复合材料的固有频率上比层合复合材料大,而且在高阶阻尼性能方面也比层合复合材料有一定的优势。纤维取向角度的变化,不但对三维四向编织复合材料的损耗因子有影响,也会对层合复合材料的损耗因子也产生重要影响。
复合材料内部阻尼取决于以下因素[11]:基体和增强体的性质和相对比例;杂质的形状尺寸;增强体相对于轴向载荷的方向;增强体的表面处理和空隙。当纤维取向角度变大时,材料振动能向热能的转换途径发生了变化,一方面是由于材料的内耗;另一方面是因为纤维与树脂间界面的变化、材料的黏弹性行为、材料的不均匀性引起的应力变化以及材料的微缺陷、损伤的产生等起的作用,这对材料的振动能量耗散也有很大影响。
在三维四向编织复合材料中,随着角度的增大,编织纱的截面形状逐渐变成圆形。此时,编织纱之间的相互作用力减小,纤维与基体之间更容易发生滑移,复合材料对振动的消耗转换变大,这些都将影响材料振动能量的耗散。即当纤维体积含量一定时,增大纤维取向角度,三维四向编织结构复合材料损耗因子增大,减振性能提高。此外,纤维体积含量一定,纤维取向角增大,编织结构的不均匀性变大,局部应力变大引起的能量耗散,也会使三维四向编织复合材料的阻尼和减振性能提高。
3.2 纤维取向角度对复合材料的抗激振性能的影响
给不同纤维取向角度的三维四向编织复合材料与层合复合材料一个较小的瞬态激励让其自由振动,记录材料的振动情况。由于结构阻尼的作用,振动逐渐衰减。这是基于在无外部周期力作用于振动试片的假设条件下,其原有的能量由于部分产生辐射和内摩擦生热而消失。因为复合材料试件的阻尼能力减弱了其自由振动,所以连续的振幅愈来愈小,直至复合材料试件恢复到静止状态。图9是三维四向编织复合材料与层合复合材料加速度衰减曲线图。从图9中可以看出,在激振力作用下,加速度响应曲线为非周期振荡曲线,并呈指数规律衰减。通过实验观察,材料的损耗因子越大,曲线衰减的越快。B-A1的初始振幅是0.4,经过大约0.2s衰减完毕;L-A1的初始振幅是0.32,经过大约0.16s衰减完毕了;B-A3的初始振幅是0.2,经过大约0.14s衰减完毕。通过比较图9中的加速度衰减曲线可知,当纤维取向相同时,三维四向编织复合材料的阻尼性能要比层合复合材料要差,振动衰减速度慢。当纤维体积含量相同,纤维取向角度不相同时,如图中的B-A3与L-A1加速度衰减曲线相比,B-A3的加速度衰减曲线明显在相同时间内比L-A1衰减快。这说明通过设计三维四向编织复合材料的编织角,可以获得满足设计要求的阻尼性能。
在模态识别中,各试样的振动功率谱曲线是由振幅的时程数据经过快速傅里叶变换得到的。振动的频谱中,功率谱值反映的振动能量在频率中的分布,频谱包围的面积表示结构振动的总能量,在相同激振条件下,振动的总能量越小,说明结构耗散的能量越多。通过模态实验,获得了材料的实频特性曲线和虚频特性曲线。在实频特性曲线中,和横坐标轴相交的零点是对应的谐振点处,为固有频率;固有频率左右的两个正负极值点为对应两个半功率点。阻尼比由半功率带宽确定,正负两极值间的水平距离越大,系统的阻尼越大。在虚频特性曲线中,负极值点处为谐振点,对应最大响应,固有频率由此时对应的负极值点确定;虚频特性曲线上负极值左右的二分之一峰值处两点为对应半功率点,阻尼比仍由公式(8)半功率带宽确定[17],即:

图9 不同纤维取向角度的三维四向编织复合材料(a)与层合复合材料(b)加速度衰减曲线图(1)A1;(2)A2;(3)A3Fig.9 Amplitude response of acceleration in time domain (a)3-dimension and 4-direction braided composites;(b)laminated composites(1)A1;(2)A2;(3)A3

以图10中,B-A1和L-A1对应的二阶固有频率对应的实频和虚频图为例。从图10可知,B-A1的二阶实频特性曲线的高度是50,虚频特性曲线的高度是45;二阶实频特性曲线的宽度是54,虚频特性曲线的宽度是36。层合复合材料L-A1对应的实频特性曲线高度是30,虚频特性曲线是25;二阶实频特性曲线的宽度是72,虚频特性曲线的宽度是46。B-A1的实频曲线高度比L-A1的高66.7%,虚频曲线高度高80%;B-A1的实频曲线宽度比L-A1的窄25%,虚频曲线宽度窄22.74%;随着纤维取向角度的增大,编织复合材料和层合复合材料所对应峰值的高都变小,极致点间的宽度都变大。B-A3的二阶实频特性曲线的高度是12,虚频特性曲线的高度是11;二阶实频特性曲线的宽度是180,虚频特性曲线的宽度是40。层合复合材料L-A3的二阶实频特性曲线高度是15,虚频特性曲线是13。二阶实频特性曲线的宽度是115,虚频特性曲线的宽度是65。B-A3的实频曲线高度比L-A3的低20%,虚频曲线高度低15.39%;B-A3的实频曲线宽度比 L-A3的宽 56.52%,虚频曲线宽度窄38.46%。随着纤维取向角度的增大,三维四向编织复合材料对应的峰值比层合复合材料更加平滑,两极值点间的距离更大。
在瞬态激振力的作用下,随着角度的增大,各阶峰值所对应的固有频率减小,损耗因子变大。当纤维体积含量相同,层合复合材料与三维四向编织复合材料具有相同的树脂基体含量,由于复合材料的阻尼特性主要取决于树脂基体的黏弹性,因此两种材料的阻尼比相互关系不变。而相同纤维体积含量条件下,两种复合材料损耗因子之间的关系取决于纤维取向角度的大小。与传统的层合复合材料相比,三维四向编织复合材料可以在较短的时间内将一定振动振幅迅速降低下来,从而减少振动的危害,这就是其作为减振复合材料使用的本质。三维四向编织复合材料的抗击激振能力更强,能够抵抗外界更剧烈的振动。

图10 不同纤维取向角度的三维四向编织复合材料(a)和层合复合材料(b)实部和虚部图;(1)A1;(2)A2;(3)A3Fig.10 The real part and imaginary part graphs of frequency response function (a)3-dimension and 4-direction braided composites;(b)laminated composites;(1)A1;(2)A2;(3)A3
4 结论
(1)纤维体积分数相同时,随着纤维取向角度的增大,三维四向编织复合材料与层合复合材料各阶固有频率都随之减小,损耗因子随之增大;纤维取向角度相同时,三维四向编织复合材料的固有频率比层合复合材料同阶次的固有频率值要大。三维四向编织复合材料的一阶,二阶损耗因子小于同阶次层合复合材料,但是三阶损耗因子大于层合复合材料同阶次损耗因子。
(2)在激振力作用下,三维四向编织复合材料与层合复合材料的加速度响应曲线为非周期振荡衰减的指数曲线;材料的损耗因子越大,曲线衰减的越快。
(3)随着纤维取向角的减小,复合材料的实部图两极值点间的距离变小表明:纤维取向角小的三维四向编织复合材料共振时幅值较大,阻尼性能较差;因此在材料的设计过程中需充分考虑抗激振性能和阻尼性能之间的相互关系,以期获得最优振动性能。
[1] 李嘉禄.三维编织技术和三维编织复合材[J].新材料产业,2010,194(1):46-49.LI Jia-lu.Three-dimensional braiding technology and three-dimension braided composites [J].Advanced Materials Industry,2010,194(1):46-49.
[2] MOURITZ A P,BANNISTER M K,FALZON P J,et al.Review of applications for advanced three-dimensional fibre textile composites[J].Composites Part A,1999,30(12):1445-1461.
[3] MAHMOOD A,WANG X W,ZHOU C W.Modeling strategies of 3Dwoven composites:a review[J].Composite Structures,2011,93(8):1947-1963.
[4] DIAN S L,LU Z X,NAN J,et al.High strain rate behavior and failure mechanism of three-dimensional five-directional carbon/phenolic braided composites under transverse compression[J].Composites:Part B,2011,42(2):309-317.
[5] 高坚新,沈亚鹏.主被动阻尼层合板结构的自由振动和阻尼特性分析[J].应用数学和力学,1999,20(10):1004-1014.GAO Jian-xin,SHEN Ya-peng.Vibration and damping analysis of a composite plate with active and passive damping layer[J].Applied Mathematics and Mechanics,1999,20(10):1004-1014.
[6] SCHULTZ A B,TSAI S W.Dynamic moduli and damping ratio in fiber-reinforced composites[J].J Composite Materials,1968,(2):368-379.
[7] HASHIN Z .Complex moduli of viscoelastic composites:I General theory and application to particulate composites[J].Int J Solids and Struct,1970,6(5):539-552.
[8] ADAMS R D,FOX M ,FLOOD R J L ,et al.The dynamic properties of unidirectional carbon and glass fiber-reinforced plastics in torsion and flexure[J].J Comp Mater,1969,3:594-603.
[9] ADAMS R D,BACON D G C.Measurement of flexural dynamic capacity and dynamic Young’s modulus of metals and reinforced plastic[J].J Phys D:Appl Phys,1973,6:27-41.
[10] ADAMS R D ,BACON D G C .Effect fiber-orientation and laminate geometry on properties of CFRP[J].J Comp Mater,1973,7:402-428.
[11] BOTELHO E C,CAMPOS A N,D BARROS E,et al.Damping behavior of continuous fiber/metal composite materials by the free vibration method[J].Composites:Part B,2006,37:255-263.
[12] 武海鹏,侯涤洋,孙立娜.玻璃纤维、炭纤维复合材料的阻尼性能分析[J].应用力学学报,2011,29(1):65-68.WU Hai-peng,HOU Di-yang,SUN Li-na.Damping analysis of glass and carbon fiber composites[J].Chinese Journal of Applied Mechanics,2011,29(1):65-68.
[13] 卢子兴,夏彪,杨振宇.三维编织复合材料悬臂梁的振动特性.复合材料学报[J].2010,27(6):172-178.LU Zi-xing,XIA Biao,YANG Zhen-yu.Vibration characteristics of 3Dbraided composites cantilever beam[J].Acta Materiae Compositae Sinica,2010,27(6):172-178
[14] 李典森,卢子兴,李嘉禄,等.三维编织复合材料振动阻尼特性的实验研究[J].机械强度,2009,31(2):211-214.LI Dian-sen,LU Zi-xing,LI Jia-lu,et al.Experimental research on the vibration damping properties of 3Dbraided composites[J].Journal of Mechanical Strength,2009,31(2):211-214.
[15] ZHANG R X,NI Q Q,MASUDA A.Vibration characteristics of laminated composite plates embedded shape memory alloys[J].Composite Structure,2006,74(4):389-398.
[16] 吕书强,李小平,瞿晓.快速傅里叶变换在振动预测中的应用[J].电气应用,2009,28(24):72-74.LV Shu-qiang,LI Xiao-ping,ZHAI Xiao.The application of Fast Fourier Transform in vibration prediction[J].Electrotechnical Application,2009,28(24):72-74.
[17] 曹树谦,张文德,肖龙翔.振动结构模态分析[M].天津:天津大学出版社,2001.13-14.

