基于并行抽样的海量数据关联挖掘算法
宛 婉, 周国祥
(合肥工业大学 计算机与信息学院,安徽 合肥 230009)
0 引 言
数据挖掘是从大量的、不完全的、有噪声的、模糊的、随机的数据提取隐含其中的、未知的、具有潜在利用价值的信息和知识的过程。关联规则挖掘是数据挖掘的一个重要分支,它通过收集数据库中大量的事物记录进行分析,查找其中有趣的关联关系,是数据挖掘的一个重要功能。但是传统的关联算法如(Apriori算法[1])在处理海量数据时,会对内存带来极大的压力。
本文对传统Apriori算法的优缺点进行详细分析,并提出了一种在海量数据并行随机抽样后,在数据抽样样本中采用MapReduce实现的并行频繁项集发现算法,其可以有效地减小对内存的压力。实验结果证明,该算法能有效提高频繁项集发现算法的运算效率,减少了内存的压力,极大地扩展了该关联算法处理海量数据的能力。
1 传统频繁集算法的局限
最经典的Apriori算法[2]主要是基于单调性理论,即:如果一个集合的子集不是频繁项集,则该集合也不可能是频繁项集。基于该思路,对所有不同的集合大小k,都要对整个数据集分别进行一遍扫描处理,如果不存在某个大小的频繁项集,则不可能存在更大的频繁项集,因此,扫描过程结束。其主要流程如图1所示,其中,Ck为大小为k的候选项集集合,即必须通过计算来确定真正频繁的项集组成的集合;Lk为大小为k的真正频繁项集集合。
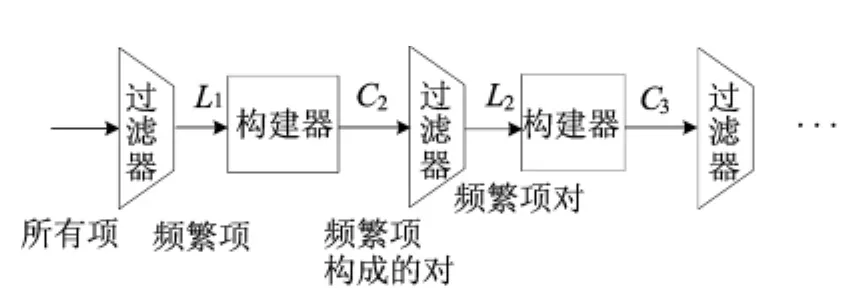
图1 Apriori算法过程示意图
上述每次扫描过程均在内存中维护很多不同的计数值。假定单元素频繁项的总数为n,在Apriori的C2扫描过程中,需要空间来存储C2n个项对计数。如果每个计数需要4字节,则共需要2n2个字节。如果单台机器为2GB,即231字节内存,则要求n≤215,即n≤33000。如果n超过该值,则在单台机器上运行传统频繁集算法会出现内存抖动现象,即在磁盘和内存之间反复传输数据,从而运行速度可能比直接在内存中运行慢几个数量级。
另外,Apriori算法利用单调性原则[3]进行剪枝,虽然已经大大减小了候选项集的个数,但在数据量大、支持度阈值较小的情况下,仍然会产生大量的频繁项集,进一步对内存提出了更高的挑战。Apriori算法是逐层扫描进行计数,在数据量较大时,扫描的代价将会相当大[4]。传统的 Apriori算法在空间(内存大小)和时间(扫描时间)上的消耗都非常大。
2 传统Apriori算法的改进
针对Apriori算法的局限,已经有多名学者对Apriori算法进行了改进,主要思想在于控制候选集的规模或减少数据集扫描次数。几种优秀的改进算法如下:杂凑表技术[5]、减少数据集的方法[6]、Partition算法[7]、抽样方法[8]、动态模式计数 法[9]、TreeProjection 方 法[10]和 FP-Growth算法[11]。
对于数据集非常大、支持度阈值相对较小的情况,上述算法存在各种各样的问题。如FP-tree算法,如果生成的条件FP-Tree非常茂盛(最坏情况下为1棵前缀树),则该算法产生大量的子问题。
为了进一步提高算法效率,有不少学者从并行化的角度来改进Apriori算法。其中比较成熟的有3种[12]:
(1)Count Distribution算法,简称CD算法。其主要聚集于最小化节点间的通信。但其在实际应用中,有可能因为计算中的I/O读写过度频繁,从而引起整体的性能下降。
(2)Data Distribution算法,简称DD算法。其先将候选项集分发到各个节点上,而获取到购物篮的统计计数。该算法需要进行大量的通信,并且等待其他节点同步信息的时间事先不可确定,所以该算法性能较差。
(3)Candidate Distribution算法,简称CaD算法。其综合了DD算法和CD算法,以弥补其各自的不足。但是该算法实现复杂,实际应用时效果不好。
由上述分析可知,以上几种并行频繁项集算法同样不能很好地满足实际应用。在面临海量数据时,当前的频繁项集挖掘算法的局限主要表现在以下3个方面:
(1)由于数据量过大,很难得知具体数据集记录条数,进而无法确定计数值阈值来产生合适数目的频繁项集。
(2)Apriori要多次扫描海量数据集来产生频繁k项集,其代价是非常大的。
(3)由频繁k项集来产生候选k+1项集,运算量大,需要内存大,耗时多。
所有研究数据均应用SPSS 17.0统计学软件进行统计分析,计量资料以(±s)表示,行 t检验,计数资料以[n(%)]表示,行χ2检验,P<0.05为差异有统计学意义。
针对以上几点,本文提出了一种基于 MapReduce编程模型的随机抽样的并行关联挖掘算法。
3 MapReduce编程模型
MapReduce编程模型[13]采用“分布治之”思想,把对大规模数据集的操作,分发给1个主节点管理下的各分节点共同完成,然后能整合各分节点的中间结果,得到最终结果,如图2所示。它有2个重要函数,可以由用户编写,即map和reduce。map负责把任务分解成多个任务,reduce负责把各个任务处理的结果汇总起来。至于在并行编程中的其他各种复杂问题,如分布式存储、工作调度、负载均衡、容错处理及网络通信等,均由MapReduce框架负责处理,可以不用程序员操心。
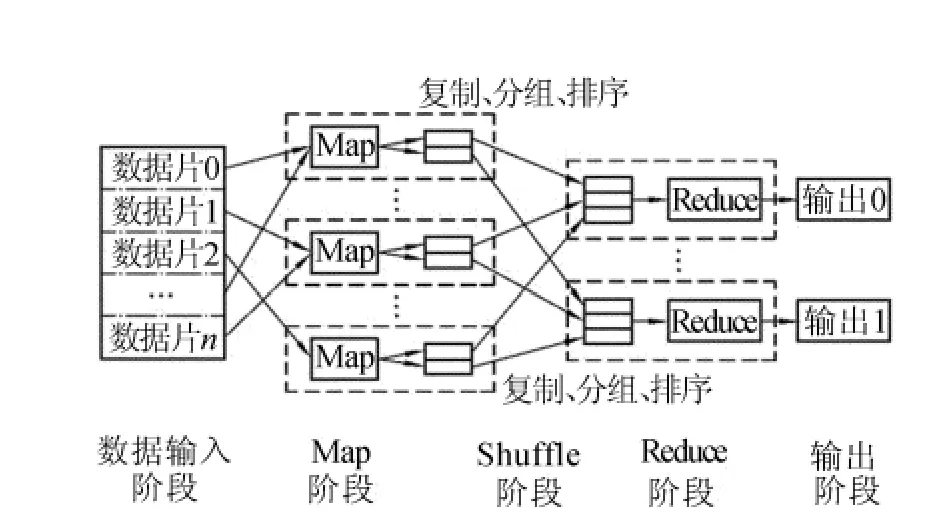
图2 MapReduce处理大数据集的过程
4 并行随机抽样算法
在传统频繁项集算法中,处理海量数据时,因为内存问题无法容纳数据和提供对某规模项集进行计数所需空间,要计算所有频繁项集不可避免需要进行k次扫描。因此可利用数据抽样样本而非数据全集来进行计算。但在现实生活中,往往很难预知所处理的海量数据所包含的记录数目(1条记录相当于1个购物篮),而数据量过大时,扫描1次代码代价非常高。所以本文提出一种在未知数据记录数目时,单次扫描即可实现随机抽样[14]并且得到样本数据的记录数目的并行算法,有效地解决了上述局限问题,保证了后续关联挖掘算法的支持度计算的正确性。设计思想为:先保存前k个元素(k为样本记录数目),从第k+1个元素开始,以1/i(i=k+1,k+2,…,N)的概率选中第i个元素,并随机替换掉一个已保存的记录,则遍历1次得到k个元素,可以保证完全随机选取。
证明 当n=k时,由前k个数放入蓄水池可知,每个样本的取出概率均相等,即k/k=1。设当前样本号为n,其每个取出样本概率均相等,即k/n,要证明这种情况对于n+1也成立。
由于以k/(n+1)来决定是否把n+1放入蓄水池,对于n+1其出现在蓄水池中的概率为k/(n+1),对于 前n个元素中的任意元素m(k+1≤m≤n),其出现在蓄水池中的概率为:
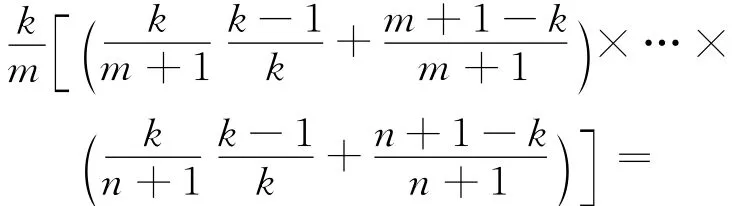
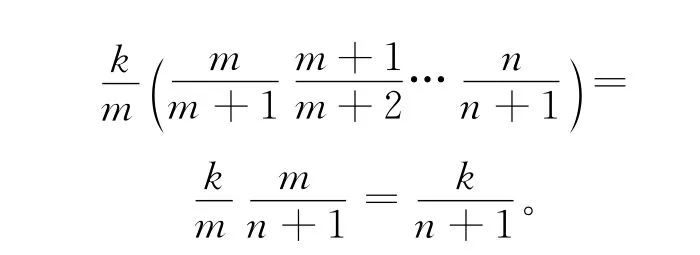
可见,对于n+1每个样本取出概率也相等,即为k/(n+1)。证毕。
要实现该并行抽样算法,只需在MapReduce框架中编写mapper即可。在map函数中,用户定义1个数组保存选中的k个元素,待扫描完所有元素后,在析构函数中将数组中的数据写到磁盘中。
5 云关联算法
运用上述并行抽样算法,在所得样本中挖掘频繁项集。本文提出了一种能运用MapReduce编程框架实现的并行频繁项集算法,在很大程度上提高了挖掘效率。
为了进一步提高效率,在map过程中添加combine过程,其主要是先对每个map任务进行相同key的value值的合并,以减少通信负载。在reduce中对这些键值对进行规约,输出支持度大于最小支持度阈值的项集,即频繁项集。再由频繁k项集生成候选k+1项集,同样采用MapReduce。
其主要思想为:由于此频繁k-项集是上一步MapReduce的输出,已经是去重有序的。本文将k-项集的前k-1项称为主模式,第k项称为从模式。在MapReduce过程中实现将主模式相同项集合并,进而得到k+1项集。具体实现步骤如下:频繁k-项集作为map任务的输入,map任务输出(前k-1项集,第k项集)的键值对,最后reduce任务进行规约,输出为{key=主模式,value=2个从模式}。
对reduce输出结果进行处理,得到k+1项集。最后将其作为下一次MapReduce的map任务的 Distributed Cache[16]和样本数据一起输入到map中继续计算频繁k+1-项集。其流程如图3所示。

图3 并行云关联算法流程
图3是一个迭代实现的过程,其结束条件为得到的频繁k-项集为空[17],则根据频繁项集的单调性,不可再有更大的频繁项集。其伪代码如下:


6 实现与分析
本文中所有的实验均在Hadoop平台上运行。其中实现时分别由2、4、6、8、10台机器组成集群。这些机器均为AMD4234双路12核构成,内存 为 16G。Hadoop 版 本 为 hadoop-0.20.2-cdh3u3,Java版本是1.6.0-31。每台机器之间用千兆以太网通过交换机连接。
实验数据是收集的应用数据,维度为30维,其大小约为150G。其中有些记录为不完全记录,即为脏数据。首先应用并行随机抽样对其进行清洗和抽样,提取其中要挖掘的一维数据。设k=100000(上述并行随机算法中的参数),则总共有465个map task。整个抽样过程花费时间仅为9419ms,约为2min。在该样本数据上分别运行改进的并行关联云挖掘算法和传统的串行Apriori算法,得出其加速比。加速比是同一个任务在单处理器系统和并行处理器系统中运行消耗的时间的比率,用来衡量并行系统或程序并行化的性能和效果。
采用不同数目的结点进行测试,其结果如图4所示。

图4 云关联算法加速比
图4结果表明,随着节点数量的增加,其运行效率成正比上升,这充分说明了并行关联云挖掘的算法非常适合进行海量数据的挖掘。
为了验证在样本空间所发现的频繁项集的正确性,本文对比在完整数据集上发现的频繁项集,给出其频繁结果的比例,见表1所列。
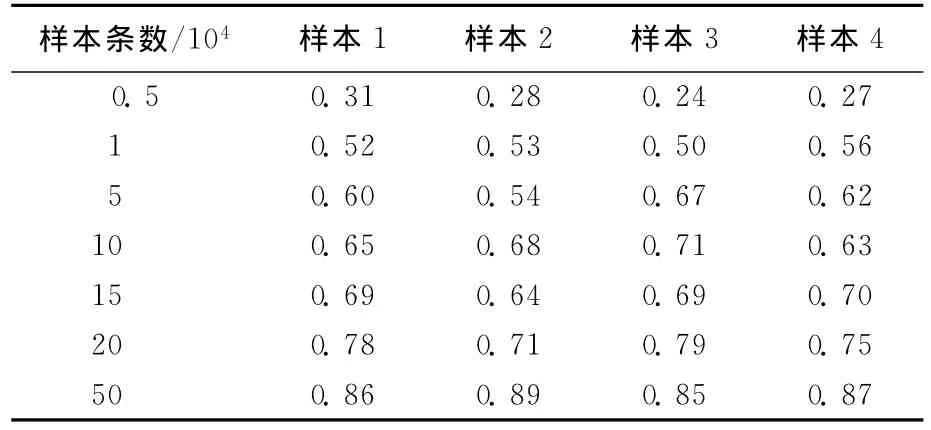
表1 样本频繁项集占完整数据频繁项集比例
为了保证其实现的准确性,分别对每种样本的大小,进行了4次随机抽样并频繁挖掘。由表1知,随着样本数的增加,其频繁项集的覆盖率正比例上升。可见,本文所提的云关联算法可以很好地适应那些挖掘实时要求高、挖掘精确性要求次之的应用。
7 结束语
本文提出了在Hadoop上运用MapReduce并行框架实现的单次扫描的随机抽样算法和利用抽样结果和MapReduce框架进行频繁项集发现的并行云关联挖掘算法。实验证明了该算法的高效性和正确性。由于是在样本数据集上进行关联挖掘,所以不可能保证会产生整个数据集上频繁的所有项集,也不能保证只产生整个数据集上的频繁项集。后续的工作将对这方面进行优化,以实现高效去除伪反例和伪正例[18]。
[1]Agrawal R,Imielinski T,Swami A.Ming associations between sets of items in massive databases[C]//Proc of the ACM-SIGMOD 1993International Conference on Management of Data,1993:207-216.
[2]Agrawal R,Srikant R.Fast algorithms for mining association rules[C]//Int Conf on Very Large Databases,1994:487-499.
[3]Tan P N,Steinbach M,Kumar V.数据挖掘导论[M].范明,范宠建,译.北京:人民邮电出版社,2012:176-180.
[4]Fang M,Shivakumar N,Garcia-Molina H,et al.Computing iceberg queries efficiently[C]//Int Conf on Very Large Databases,1998:299-310.
[5]Park J S,Chen M S,Yu P S.Efficient parallel data mining of association rules[C]//4th International Conference on Information and Knowledge Management,1995:233-235.
[6]Han Jiawei,Kamber M.数据挖掘概念与技术[M].范 明,孟小峰,译.北京:机械工业出版社,2001:149-175.
[7]Savasere A,Omiecinski E,Navathe S B.An efficient algorithm for mining association rules in large database[C]//Int Conf on Very Large Databases,1995:432-444.
[8]Toivonen H.Sampling large database for association rules[C]//Int Conf on Very Large Databases,1996:134-145.
[9]Brin S,Motwani R,UIIman J K,et al.Dynamic itemset counting and implication rules for market basket data[C]//ACM SIGMOD International Conference on the Management of Data,1997:255-264.
[10]Agarwal R C,Aggarwal C C,Prasad V V V.A tree projection algorithm for generation of frequent itemsets[J].Journal of Parallel and Distributed Computing,2001,61(3):350-371.
[11]李志云,周国祥,张丽萍.一种挖掘大型数据库的关联规则新算法[J].合肥工业大学学报:自然科学版,2010,33(2):204-207.
[12]赵 虎.云计算环境下的关联数据挖掘算法实现[D].成都:电子科技大学,2011.
[13]Dean J,Ghemawat S.Mapreduce:simplified data processing on large clust[J].Communications of the ACM,2008,51(1):107-113.
[14]高纳德.计算机程序设计艺术 [M].北京:国防工业出版社,2007:657.
[15]Apache Software Foundation.Hadoop streaming [EB/OL].[2011-12-23].http://hadoop.apache.org/common/docs/r0.15.2//streaming.html.
[16]李建江,崔 健,王 聃,等.MapReduce并行编程模型研究综述[J].电子学报,2011,39(11):2635-2642.
[17]秦如新,陈 静,冯一宁.一种新的关联规则抽样算法[J].中国农业大学学报,2007,12(3):85-88.
[18]Rajaraman A,Jeffrey D U.Mining of massive datasets[M].Cambridege:Cambridge University Press,2012:167.

