一类欠驱动系统的全局改进积分模糊滑模控制
杨兴明, 杨传伟, 马文森
(合肥工业大学 计算机与信息学院,安徽 合肥 230009)
0 引 言
不确定系统的研究一直以来被认为是现代控制理论的主要课题。滑模控制是一种具有较强鲁棒特性的非线性反馈控制技术,理想滑模控制过程中总是假设控制器能够快速地在有限时间内从一种结构切换到另一种结构。然而,由于实际控制器不可能快速地切换控制信号,这就导致控制器输出出现抖动现象[1-2]。通常的解决方法是在滑模面附近引入边界层[3-4],然而在系统不确定性和外界扰动存在时,该方法将会导致系统稳态误差的存在[5]。
为减少系统的稳态误差,通常可以在滑模控制器中引入积分环节。但初始误差和扰动较大时,积分会出现饱和效应,产生较大的超调量和调整时间,影响系统的动态性能。文献[5]中设计了一种改进积分滑模控制方式,通过调整因子的选取来对边界层外的积分项进行削弱,一定程度上既防止积分饱和引起大的超调,也减少了性能的损失[5]。但就欠驱动系统而言,即使可以根据实际情况对调整因子进行选取,也很难获得满意的动态特性。
本文以一类欠驱动不确定系统为研究对象,结合改进积分滑模方式和全局积分滑模方法设计一种控制方法,它在保证系统鲁棒性的基础上使系统获取好的暂态特性,最后给出作为一类典型欠驱动不确定性系统两轮移动小车的仿真结果。
1 模型描述
考虑一类欠驱动不确定性系统如下:
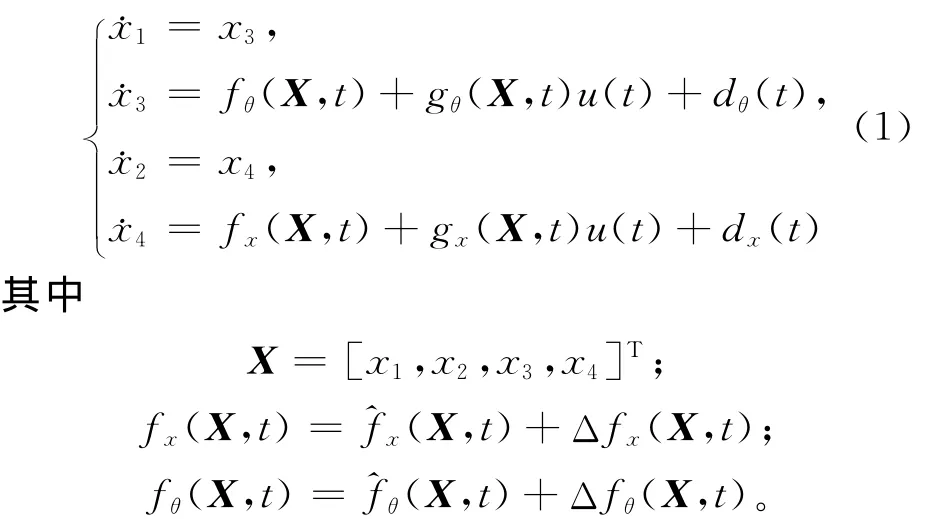
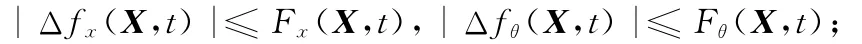
gx(X,t)、gθ(X,t)为已知的非线性函数;dx(t)、dθ(t)为外在的干扰,假设其界限范围为已知,即

对两轮移动小车而言,考虑两轮移动小车系统模型绕Y轴旋转状态转移矩阵为常数,不存在不确定性,且控制比较简单,故重点放在系统的位移和摆杆角度状态控制过程[6]。对应(1)式中的参数表达式如下:
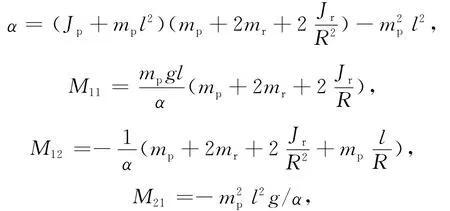
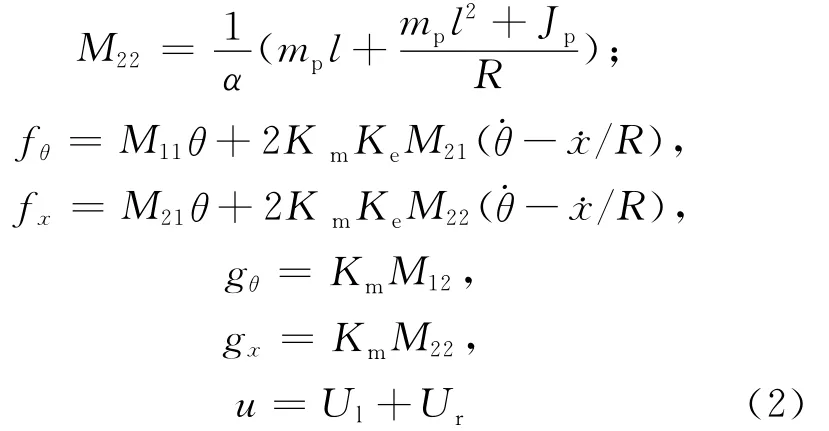
其中,θ为摆杆与竖直方向的角度;mp、mr分别为车体质量和小轮的质量;Jr、Jp分别为小轮绕轴的转动惯量和车体绕电机轴的转动惯量;R为车轮半径;l为车体重心到电机轴线之间的距离;Km、Ke分别为电机的力矩系数和电机的反电动势系数;Ul、Ur分别为左右电机的控制电压。
2 传统滑模控制器
设ex=x-xd,eθ=θ-θd为系统的角度和位移输出误差,考虑到系统零状态的动态性能,设计传统滑模面[7]为:
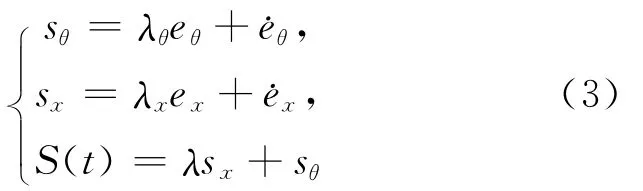
其中,λx、λθ、λ为待设计的滑模面常数。
为了抑制控制律不连续性导致的抖动现象,通常在滑模面附近引入边界层,即以脉冲函数取代不连续的符号函数。此时控制律描述为选择控制律,即
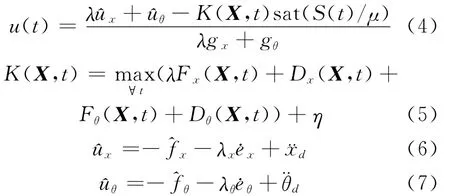
其中,μ>0为边界层宽度;η为正常数;sat函数被定义为:
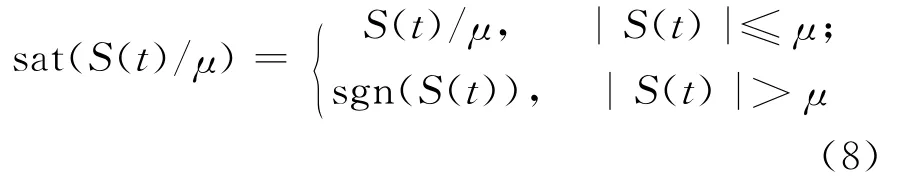
令李雅普夫函数为Vs=0.5S2(t),则其沿轨迹(3)式求导得:

即系统可以在有限时间内稳定到滑模面上。
对于欠驱动系统如(1)式,采用(3)式定义的传统耦合滑模面,在控制(4)式作用下系统是存在稳态误差的,且和边界层的宽度成正比[5]。为减少稳态误差,必须减少相应的边界层宽度,但是过小的边界层又会增加控制输出的抖动现象。
为解决这种矛盾,通常会在传统滑模面中引入一个跟踪误差的积分项。与传统滑模面相比,积分型滑模面的控制器可以更好地减少系统的稳态误差,然而在大的初始误差和扰动下,积分会出现饱和效应,引起大的超调和驱动机构的饱和,甚至使整个系统不稳定[8]。
3 全局改进积分模糊滑模控制器
积分饱和现象,主要源于被用于闭环控制器中减少系统静态误差的积分器。当执行器受限,输出误差增大时,积分器将输出更大的幅度,以至即使输入已出饱和区,控制器却因初始状态而给出错误状态,输出超调增大,调整时间也延长[9]。为此本文受文献[5]的启发,设计了一种全局改进积分滑模控制方式。同时,考虑到边界层外部时,对于调整因子削弱积分环节的程度没必要进行定量、精确的处理[10]。所以,本文设计一个二维模糊系统根据系统状态来自适应该调整因子。设计的全局改进积分模糊滑模控制系统如图1所示。

图1 全局改进积分模糊滑模控制系统
3.1 全局改进积分滑模控制器设计
为了消除积分项初始时刻误差引起的超调和控制信号过大的问题[11],设计的全局滑模面[5]如下:

选择控制律为:

其中,si表示sx、sθ。
令李雅普夫函数为Vs=0.5S2(t),则其沿轨迹(10)式求导可得:

即在控制律(11)式作用下,滑模变量可以稳定到滑模面上。
3.2 稳态误差及调整因子ρ分析
3.2.1 稳态误差分析
定义γ、w(X,t)如下:

定理1 对于非线性欠驱动系统如(1)式,选用控制律(11)式,当t→∞时,若外界干扰为常值,或稳定为常值时,则其稳态误差趋近于0,即
证明 当系统滑模变量进入边界层时,由(10)式、(11)式、(16)式和(17)式可得:
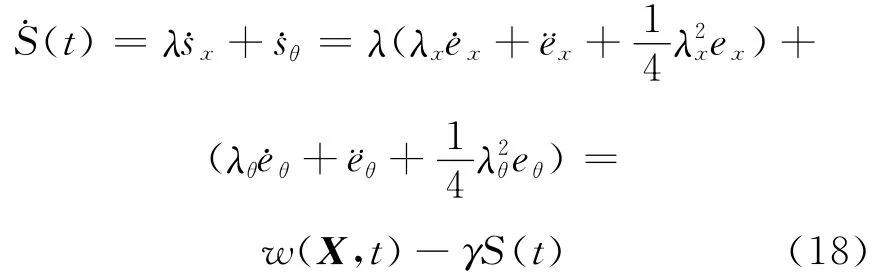
因为S(0)=0,对(18)式拉普拉斯变换得:
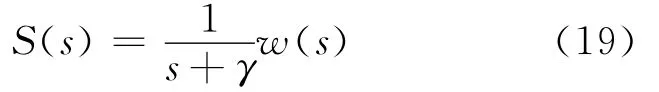
其中,s为Laplace算子。

显然,˙s(t)一致连续,当t→∞时,将(20)式带入(18)式中,有˙s(t)→0,即
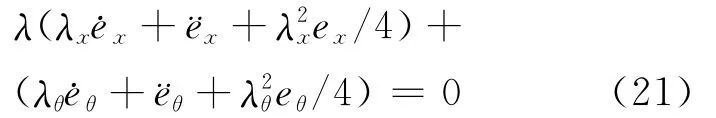
对(21)式拉氏变换有:
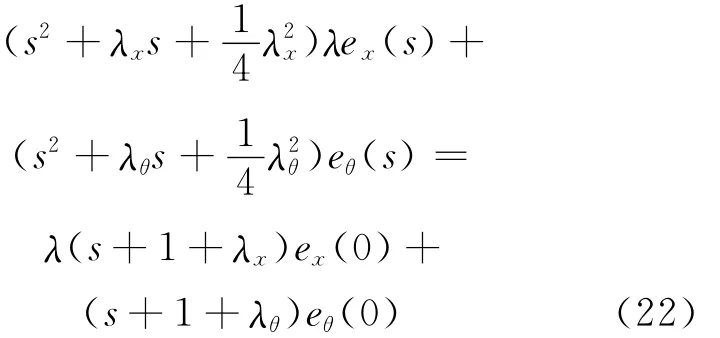
为了方便分析,对于(22)式,令λx=λθ=C,C为非零常数,则

根据终值定理有:
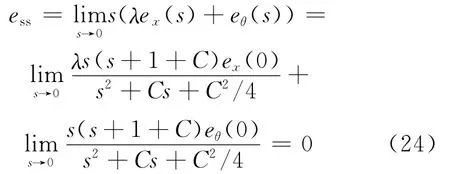
3.2.2 调整因子ρ
若ρ=0时,系统即为传统的积分滑模形式。当|si|≤μ,即在边界层内部时,为一般的积分环节。一旦超出边界层,积分操作就会减弱,其削弱程度为这样由于ρ的过渡作用不会使控制量产生跳变,柔化了控制输入。
针对ρ的范围[8],由(14)式可知,为保持积分项所起的加速作用,ei应与ei±ρ(|si|-μ)/λi具有相同符号,即

实际选取时可以结合模糊子系统中|si|-μ的论域范围、初始态误差及λi确定ρ的大概范围。
3.3 模糊接口子系统
从边界层对积分项的削弱到边界层内的传统积分,调整因子ρ起了重要作用。ρ越大,系统就具有越强抗饱和特性,但会影响系统的响应速度。
定义ρ为:

其中,ρb为ρ的调整基值;B为ρ的调整幅度;Δρ为变化范围。
在设计的模糊接口系统中,|si|-μ表示滑模变量si距相应边界层的距离,作为二维模糊接口系统的输入,Δρ为模糊接口系统的输出。
模糊输入和输出定义的模糊集为{L,L-,M,S+,S},模糊控制器的输入|si|-μ的论域为[0,1],输出Δρ的论域为[0,1]。隶属度函数采用均匀分布的三角形函数。
模糊控制器采用Mamdani型模糊推理系统,输入用单值模糊化,推理用最大最小合成规则,输出用重心解模糊的方法[12]。模糊控制规则见表1所列。
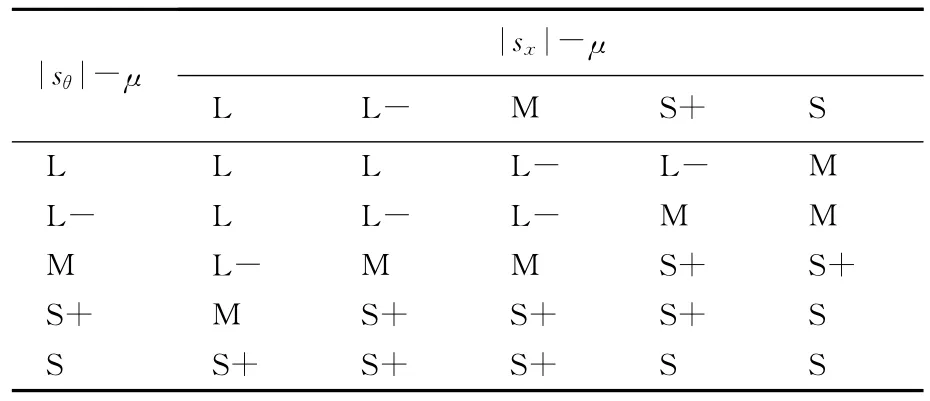
表1 Δρ模糊控制规则
4 两轮移动小车的控制效果仿真
4.1 仿真参数选取
实际模型参数如下:
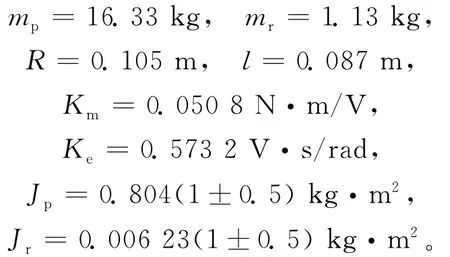

仿真时不确定性干扰参数、控制器参数等选取如下:
(1)不确定性干扰参数。参数Jp、Jr所引起的系统的不确定矩阵为:

则系统的不确定性干扰可以表示为:
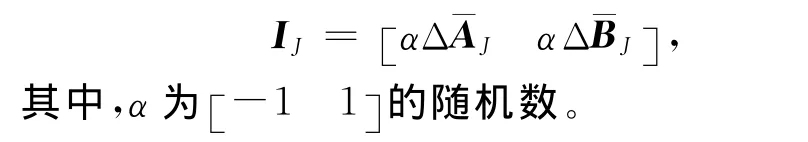
(2)控制器参数。参数λx、λθ、λ的选取决定滑模面的性能特性。采用极点配置的方法[13]选择极点[-9+j,-9-j,-1.5+j,-1.5-j],这样选取的系数可以使滑模变量运动会沿着设计的特性运行,满足系统既定设计的性能指标。仿真时选取的参数为:
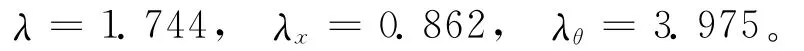
其他控制器参数选取为:

4.2 控制效果仿真
选择下面3种控制器进行仿真[14]。
方式C1 采用传统滑模面,滑模面选择为:

方式C2 采用改进积分滑模面,滑模面选择为:
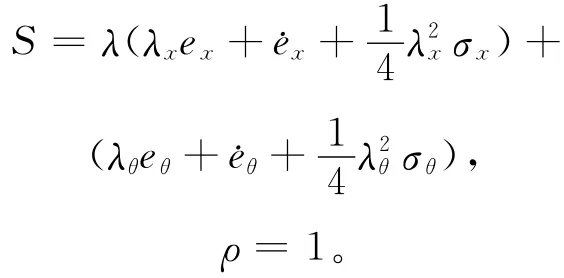
方式C3 采用全局改进积分模糊滑模面,滑模面选择为:

并且引入自适应参数ρ,ρ通过模糊控制接口系统在线调整。
下面分别就两轮移动式小车自平衡过程和移动过程进行仿真。
(1)假设系统初始状态 X=[0.3000]T,即摆杆偏移0.3rad(17°),同时在整个过程中引入系统不确定性干扰IJ。仿真系统的摆杆角度曲线、系统速度趋近平衡过程曲线和方式C3中的调整因子变化曲线如图2所示。

图2 自平衡过程仿真结果
图2a和图2b中,在系统不确定性干扰IJ下,全局改进积分模糊滑模控制方式C3能够比较平稳和光滑地趋近指定状态,比其他2种方法具有较快的响应速度和较小的超调量,表现出良好的鲁棒性。
(2)假设设定系统在2s跟踪0.5m/s的速度运行,并在10s时上斜度为15°的坡,同时在整个过程中都引入系统不确定性干扰IJ。仿真系统移动时的摆杆角度曲线、系统速度响应曲线和方式C3中调整因子变化曲线如图3所示。
由图3a可知,系统2s时开始进入跟踪阶段,然后会进入自平衡过程,在10s时由于上坡影响,摆杆会有一个固定的角度偏移(即上坡时摆杆会有前倾的现象)。图3c中调整因子最后稳定为一常数值,这是由于系统在上坡过程中,坡度可以理解为对系统不确定性的一种常值干扰,会使系统滑模面产生一种稳定的误差,而模糊因子稳定为一常值,正是为了调整这种系统不确定性干扰的影响。

图3 移动过程仿真结果
5 结束语
本文为控制一类欠驱动不确定性系统,设计了一种全局改进积分模糊滑模控制方法,该控制方法不仅保持了传统滑模的鲁棒性优点,还改善了系统的暂态特性,提高了控制精度;最后分别对小车系统自平衡过程和移动过程做了仿真分析,通过仿真可知,在系统受到外界干扰的情况下,该方法能够使系统获得较好的鲁棒特性和较小的超调量,从而验证了该方法的有效性。
[1]高为炳.变结构控制的理论与设计方法[M].北京:科学出版社,1996:205-233.
[2]刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3):407-418.
[3]Bartolini G,Ferrara A,Usai E.Chattering avoidance by second order sliding mode control[J].IEEE Trans Automat Control,1998,43(2):241-246.
[4]Kachroo P,Tomizuka M,Chattering reduction and error convergence in the sliding mode control of a class of nonlinear systems[J].IEEE Trans Automat Control,1996,41(4):1220-1226.
[5]李 鹏,马建军,李文强,等.一类不确定非线性系统的改进积分型滑模控制 [J].控制与决策,2009,24(10):1463-1472.
[6]陈 星,魏衡华,张玉斌.两轮行走倒立摆系统的建模与鲁棒方差控制[J].计算机仿真,2006,23(3):263-266.
[7]Wang W,Yi J,Zhao D.Design of a stable sliding-mode controller for a class of second-order underactuated systems[J].IEEE Proc Control Theory,2004,151(6):683-690.
[8]李 鹏,孙未蒙,李文强,等.一种改进积分滑模面在飞控中的应用[J].控制工程,2010,17(3):269-289.
[9]王军霞,朱群雄,耿志强.一种解决输出超调问题的滑模流行新算法[J].控制工程,2012,19(1):77-80.
[10]乔 枫,郭慧佳,李界家,等.二级倒立摆系统的模糊滑模变结构控制[J].沈阳建筑大学学报:自然科学版,2010,26(4):792-797.
[11]熊 柯,夏智勋,郭振云.倾斜转弯高超声飞行器滚动通道的自适应全局积分滑模控制[J].国防科技大学学报,2012,34(2):114-118.
[12]柳 波,王 浩,高 宇,等.膨胀节成型机模糊自适应趋近律滑模控制研究[J].合肥工业大学学报:自然科学版,2012,35(4):463-466.
[13]Ackermann J,Utkin V.Sliding mode control design based on Ackermann’s formula[J].IEEE Trans on Automat Control,1998,43(2):234-237.
[14]刘金琨.滑模变结构控制 MATLAB仿真[M].北京:清华大学出版社,2005:397-438.

