吸力控制下非饱和土的动力特性①
薛 龙
(同济大学地下建筑与工程系,上海 200092)
0 引言
一般而言,地下水位以上的浅层土均处于非饱和状态,其性质与饱和土差异较大.在基坑工程中,地基非饱和土的基质吸力所产生的抗剪强度对于基坑的稳定有很大的贡献;同样,许多天然边坡的失稳常常是由于降雨使土体的基质吸力下降所造成的.在地震、风浪、交通、打桩、机器基础等振动荷载的作用下,土的强度和变形特性都会受到较大影响,与静荷载作用下的性质差异较大.随着高速公路、铁路、地下隧道的飞速发展,使得非饱和土动力特性的研究具有非常重要的工程意义.
上世纪六十年代开始,国内外学者开始了对非饱和土动力特性的研究工作.1966年,Hardin和Black[1]通过共振柱试验得出饱和土的动剪切模量与等效有效应力有关.1974年,Anderson和Richart[2]提出了饱和粘土的剪切模量与试样温度的关系.1979 年,Roesler[3]通过剪切波速的方法得出了动剪切模量与孔隙水压力和气压力有关.1984年,吴世明等人[4]给出了剪切模量与饱和度的关系曲线,提出了最优饱和度的概念,即在土样的饱和度达到5%~20%之间的某一值时,土的动剪切模量出现最大值.同时,他有给出了土颗粒的有效粒径和最大动剪模量比的线性关系.1993年,钱学德[5]提出了非饱和土的动剪切模量和饱和度,围压,孔隙比,颗粒形状和粒径的关系曲线.他指出,孔隙压力在很大程度上提高了非饱和土的动剪模量,并且,最大动剪模量与土样的孔隙比存在一定的线性关系;随着围压的提高,剪切模量与最大动剪模量的比值减小,但不影响最优饱和度的值;土颗粒粒径越小,土的最大动剪模量比越大.2007年,王猛等人[6]通过动剪扭试验得出了循环荷载条件下,非饱和土的应力—应变骨干曲线,建立了应力—应变骨干曲线的等价粘弹性模型.2008年,杨庆等人[7]提出围压和基质吸力对非饱和粉土动强度的影响情况,在其他条件不变的情况下,围压越大,基质吸力越大,非饱和粉土的动强度越大.
本文以非饱和粉砂为研究材料,利用非饱和土动静三轴仪,在3种不同净应力和5种不同基质吸力的工况下,通过循环荷载下的动三轴试验对试样进行分析,并计算其动弹性模量与阻尼比,并讨论了它们随着动应变、净应力、基质吸力的变化规律.
1 试验材料和试验方法
1.1 试验材料
本论文所有试验用土均为取自日本的名为DL-clay的粉砂.各个试样的物理参数详见表1.
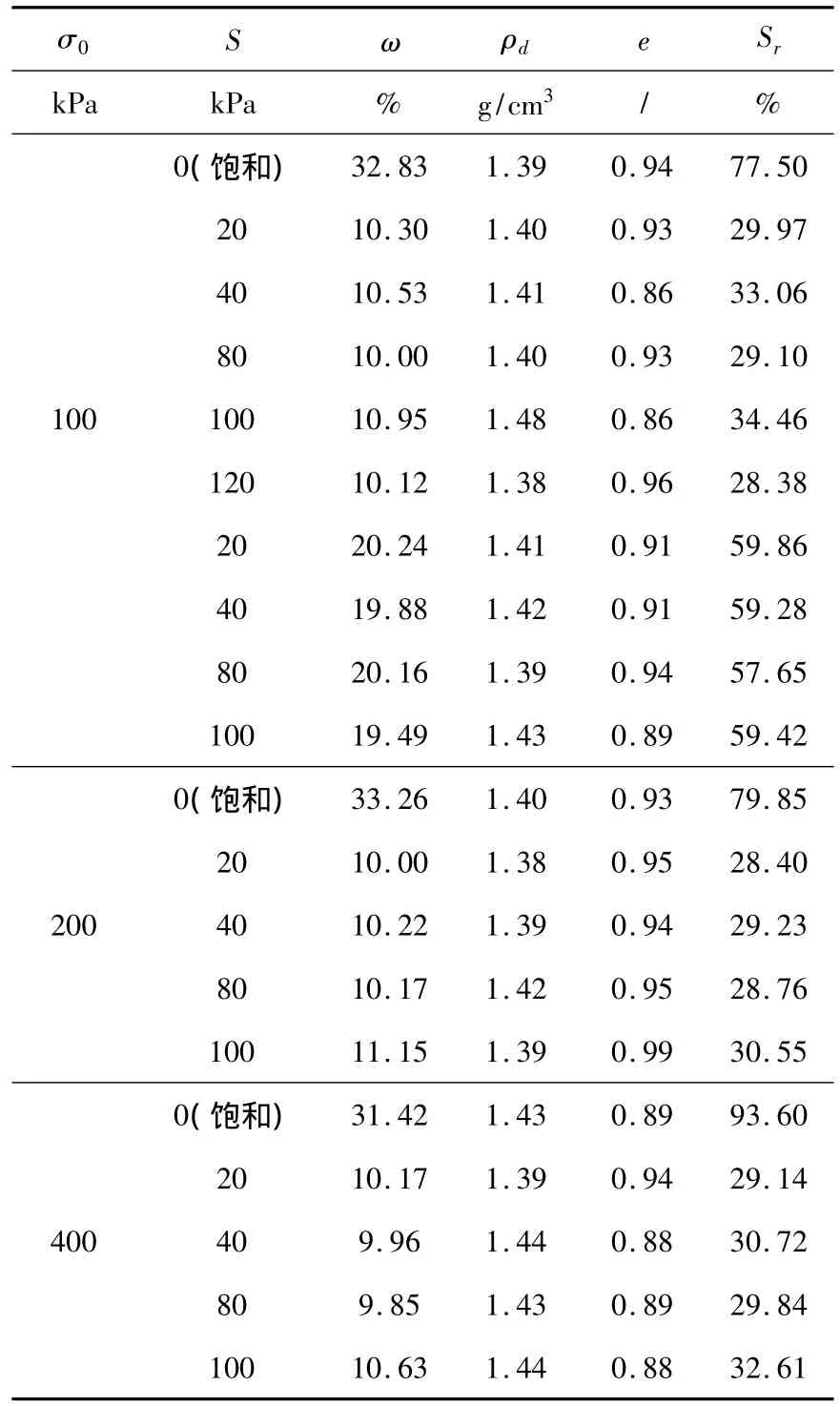
表1 各工况试样的物理参数
土样的土水特征曲线如图1所示:
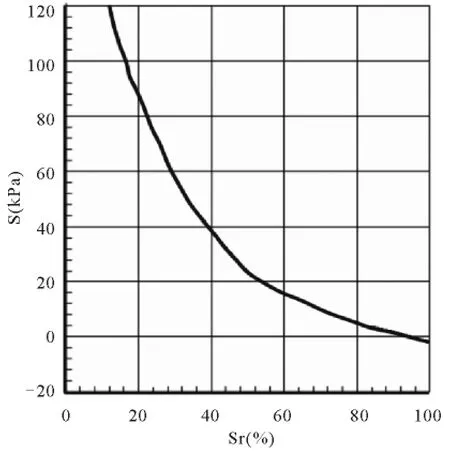
图1 DL-clay的土水特征曲线
试样为圆柱形,直径为50mm,高度为100mm.将完全干燥的粉土按含水率为10%和20%的比例进行配土,然后置于保鲜袋内存放24h,使土样内水分完全均匀.接着采用内径为50mm的两瓣膜制样器,将土样用击实锤击实.之后对试样进行固结,值得注意的是,试样底座的陶土板必须处于饱和状态,否则水分不能及时通过陶土板,导致孔隙水压力读数不准,影响吸力值.
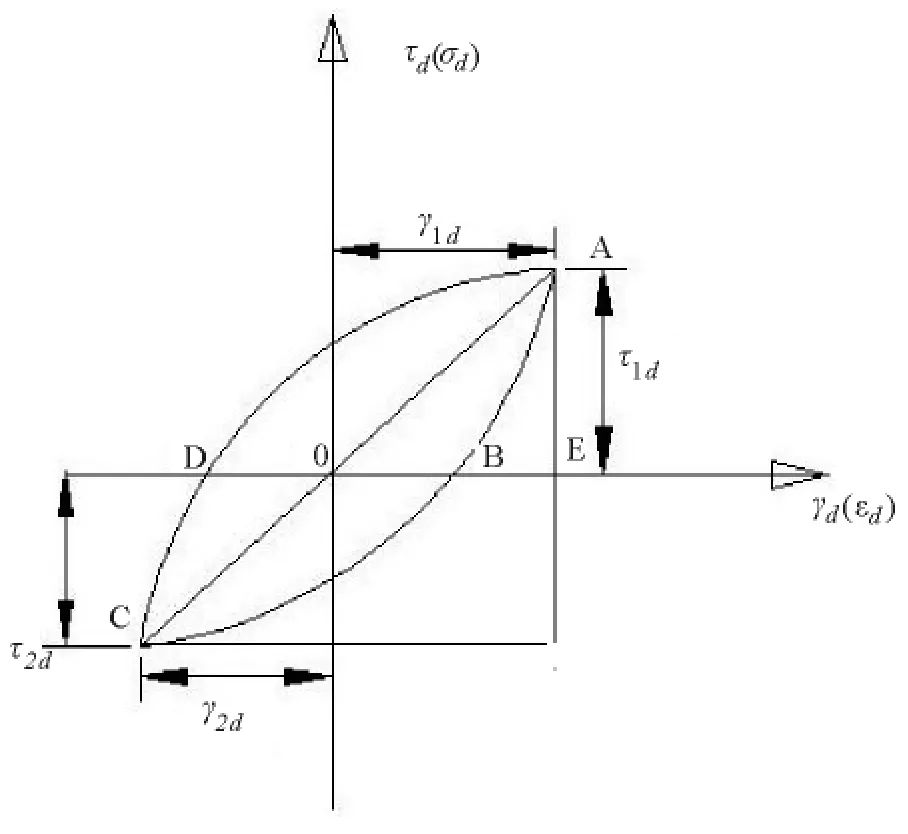
图2 理想的应力应变滞回圈
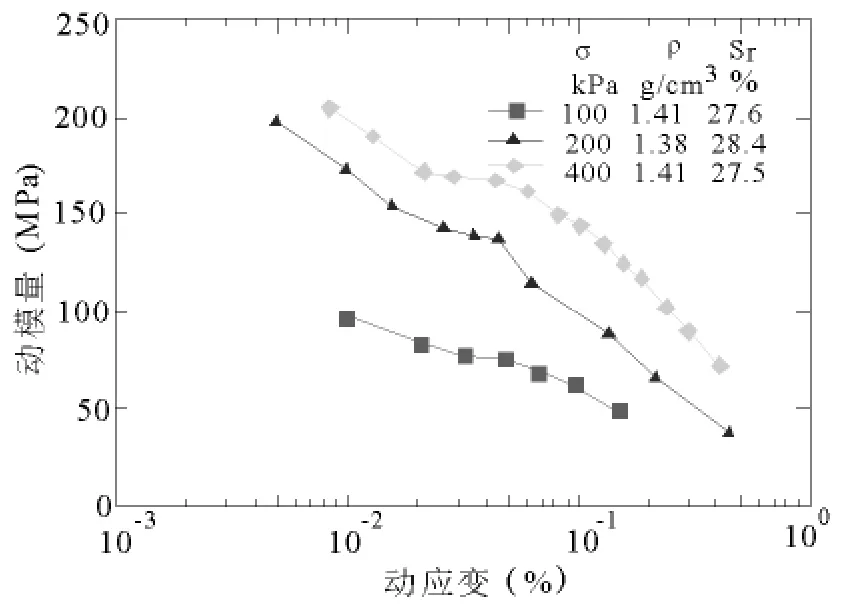
图3 动模量-动应变关系曲线

图4 动模量-净应力关系曲线
1.2 试验方法
采用动三轴试验测定土的动模量和阻尼比,是目前常用的一种方法.试样制备、固结后,在不排水条件下施加轴向循环荷载,测记试样在每一循环荷载作用下的动应力和轴向应变的时程曲线,绘制出一条滞回曲线.
试验采用同一个试样,在同一固结压力下,改变5-6级动荷载连续进行试验的方法.荷载采用正弦变化的等效循环荷载,固结应力比Kc=1;振动试验采用固结不排水振动;动荷载频率取0.5Hz.动应力分级加载,每级振动11次,施加完一级动荷载,等消除孔隙水压力后,再施加另一级荷载.
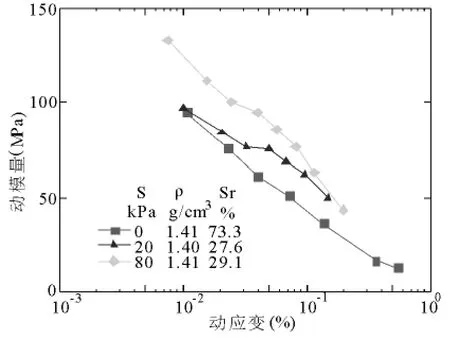
图5 不同吸力下的动模量-动应变关系曲线
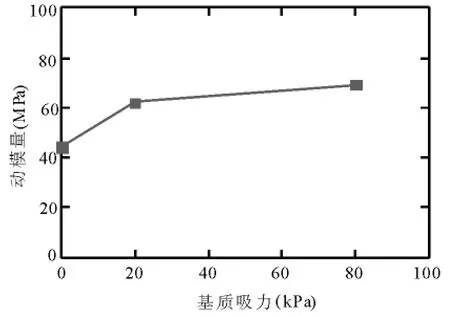
图6 动模量-基质吸力关系曲线(应变10-3)
2 试验结果分析
2.1 动弹性模量特性
土工试验规程规定[9]根据所采用的x,y轴坐标不同,滞回圈两端的斜率被定义为动弹性模量Ed:

式中:σd,εd分别为轴向动应力和轴向动应变.
理想的循环应力-应变滞回曲线如图2所示,Hardin[10]将动剪切模量和阻尼比定义如下:

式中:τ1d,τ2d分别为正负最大循环剪应力;γ1d,γ1d分别为正负最大循环剪应变.
根据Hardin的定义,本试验的动弹性模量Ed计算如下:

式中:σdmax和σdmin分别为每次循环中土样的最大与最小动应力,εdmax和εdmin分别为其所对应的动应变.

图7 阻尼比-动应变关系曲线
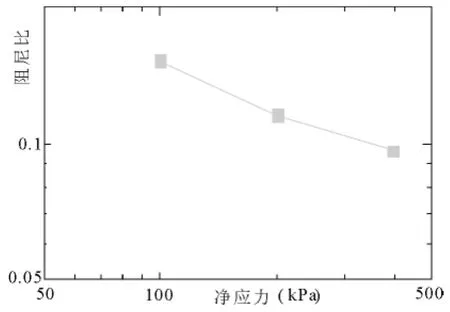
图8 阻尼比-净应力关系曲线(应变10-3)
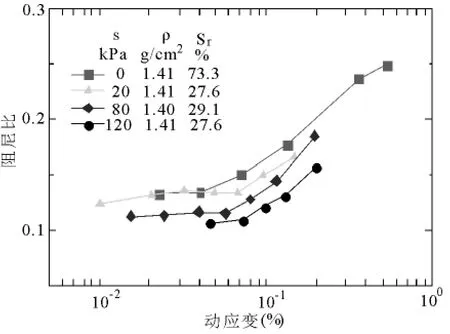
图9 阻尼比-动应变关系曲线
2.2 不同净应力下的动弹性模量-应变曲线(基质吸力为20kPa土样)
由图3,4可知:在相同的净应力条件下,动模量随着动应变的增大而减小;在相同的动应变条件下,动模量随着净应力的增大而增大,但是增大的趋势逐渐减小.
2.3 不同吸力下的动弹性模量-应变曲线
由图5可知:在相同净应力下,动模量随着基质吸力的增大而增大.取动应变为10-3,画出动模量-基质吸力关系曲线(图6)可知,随着基质吸力的增大,动模量的增大趋势逐渐减小.
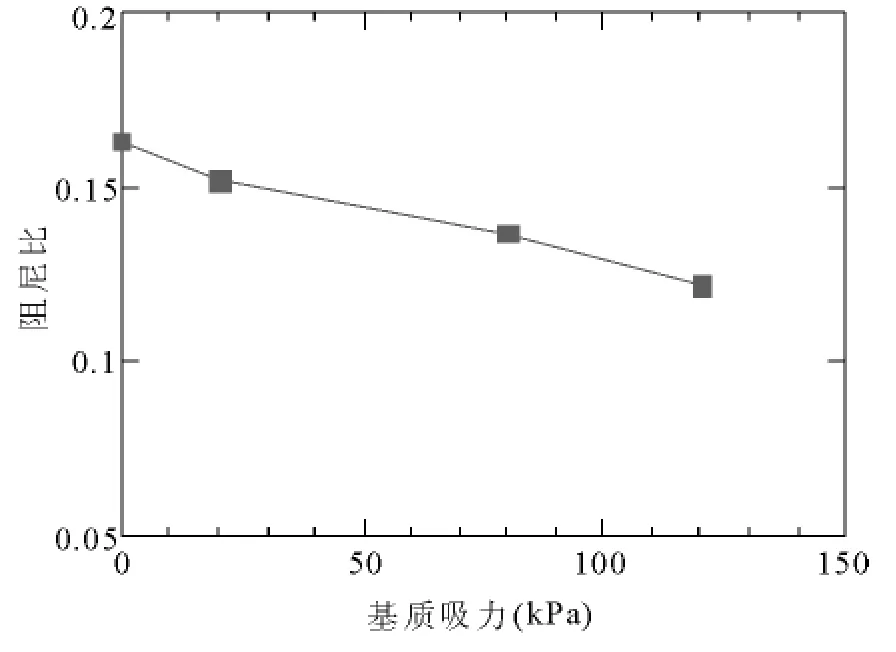
图10 阻尼比-基质吸力关系曲线(应变10-3)
2.4 阻尼比
通过一个周期内不同时刻对应的动应力和动应变作出的动应力 -动应变滞回曲线(图2所示)还可以求得阻尼比λ:

式中:A表示滞回圈ABCD的面积,As表示滞回圈顶点至原点连线与横轴形成直角三角形OAE的面积
基质吸力为20kPa的试样的实验曲线如图7~11所示,由图可知:
(1)在净应力一定的条件下,阻尼比随着动应变的增大而增大.当动应变较小时,阻尼比的增大趋势较为平缓;当动应变超过一定数值时,阻尼比的增大趋势较为明显.
(2)阻尼比受净应力的影响很明显.在相同的动应变下,净应力越大,阻尼比越小.而且,在一定应变范围内,lg D和lgσ0为线性关系.
(3)阻尼比随着试样基质吸力和饱和度的增大而增大.

图11 不同饱和度下的阻尼比-动应变关系曲线
3 结论
本文以非饱和粉砂为研究材料,在3种不同净应力5种不同基质吸力的工况下,对试样进行循环荷载下的动三轴试验,得出了非饱和粉砂的动弹性模量与阻尼比,并讨论了它们随着动应变、净应力、基质吸力的变化规律.总结本文主要研究成果,得出以下主要结论:
(1)在其他条件一定的情况下,动弹性模量随着动应变的增大而减小,随着净应力和基质吸力的增大而增大,但是增大的趋势均逐渐减小.最大动弹性模量随着净应力和基质吸力的增大而增大,增大的趋势逐渐减小.
(2)在其他条件一定的情况下,阻尼比随着动应变的增大而增大;当动应变较小时,阻尼比的增大趋势较为平缓;当动应变超过一定数值时,阻尼比的增大趋势较为明显.在相同的动应变下,阻尼比随着净应力、基质吸力、饱和度的增大而增大.
[1]Hardin,B.O.and Black,W.L.Sand Stiffness under Various Triaxial Stresses[C].Proc.ASCE,1966,Vol.92,SM2,pp.27-42.
[2]Anderson,D.G.and Richart,F.E.J r.Temperature Effect on Shear Wave Velocities in Clays[J].Journal of the Soil Mechanics and Foundations Division,1974,Vol.100,No.12,pp.1316-1320.
[3]Roesler,S.K.Anisotropic Shear Modulus Due to Stress Anisotropy[J].Journal of the Soil Mechanics and Foundations Division,1979,Vol.105,No.7,pp.871 -880.
[4]Wu,S.,Gray,D.H.and Richart,F.E.Capillary Effects on Dynamic Modulus of Sands and Silts[J].Journal of Geotechnical Engineering Division,ASCE,1984,110(9):1188 -1203.
[5]Qian,X.,Gray,D.H.and Woods,R.D.Resonant Column Tests on Partially Saturated Sands[J].Geotechnical Testing Journal,1991,14(3):266 -275.
[6]王猛,杨庆,聂影,张小玲.非饱和黏土动力特性及等价粘弹性模型的试验研究[J].岩土力学,2009,30(4):926-932.
[7]杨庆,王猛,栾茂田,刘功勋.非饱和粉土静、动强度对比试验研究[J].岩土力学,2010,31(1):71-75.
[8]谢定义.土动力学[M].西安:西安交通大学出版社,1988.
[9]南京水利科学研究院土工研究所.土工试验技术手册[M].北京:人民交通出版社,2003.
[10]Hardin B.and Drnevich V.Shear Modulus and Damping in Soils:Measurement and Parameter Effect[J].Journal of the Soil Mechanics and Foundation Engineering Division,1972,98(6):603-624.
[11]何荣昌.动模量和阻尼的动三轴试验研究[J].岩土工程学报,1997,19(2):39 -48.

