树指标集马氏链的强极限性质

边 静，汪志明

（唐山学院 基础教学部，河北 唐山063000）

1 预备知识

设T是一无限树，x≠y是T的两个不同顶点，在顶点x和y 之间存在唯一的路径：x＝z1，z2，…，zn＝y，其中z1，z2，…，zn是不同的顶点，并且zi和zi＋1相邻。于是x和y之间的距离为n－1。为了给树T中的顶点编号，我们选定一顶点为根顶点，记为O。如果一个顶点和根顶点O的距离为n，称该顶点为第n层顶点，称根顶点O为第0层顶点。

树指标集马氏链［1］的概念首先由Benjamin I．提出来，杨卫国研究了齐次树指标集马氏链的若干极限性质［2］，在此本文将定义一类特殊的非齐次树，并给出非齐次树指标集马氏链的强极限性质。

定义 设T是一无限树，｛Nn，n≥1｝为一可数的正整数集合，如果对于n（n≥0）层的顶点都有Nn＋1个子代，树T为广义的Bethe树或广义的Cayley树。特别的，令N＝｛0，1，2…｝，用模r（正整数）的同余关系对其分类得到r的剩余类：

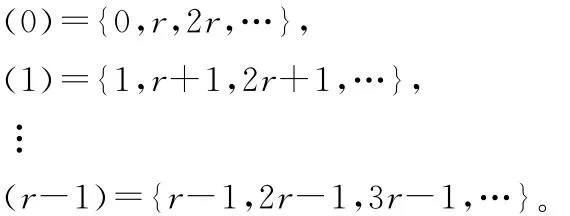
当n∈（i），令 Nn＋1＝αi（αi为正整数，并且不恒为1）。i＝0，1，…，r－1。用这种方法，我们得到了特殊的非齐次树 Tα0，α1，…，αr－1 。

在本文中，T 表示非齐 次树 Tα0，α1，…，αr－1，G＝｛0，1，2，…｝为一可数集合，｛Xσ，σ∈T｝是定义在概率空间｛Ω，F，P｝上在G中取值的树T指标集马氏链。Tn表示从根顶点到第n层的顶点组成的子树。T（i′）n（i′＝0，1，2，…，r－1）表示由根顶点到第n层顶点之中第（i′）层上的顶点构成的子树。S（σ）为顶点σ的所有子代。

引理［3］设｛ξn，n≥0｝为关于｛Fn，n≥0｝适应的随机序列，且对于n＞0，都有常数K＞0，使得｜ξn｜≤K，设｛an，n≥1｝是任一非负的随机变量序列。令

2 非齐次树指标集马氏链的强极限定理

定理1 设｛Xσ，σ∈T｝为非齐次树T指标集马氏链，｛an，n≥1｝为任意的随机序列。g（x0，x1，…，xr－1）为定义在Gr且取值0或1的函数。设

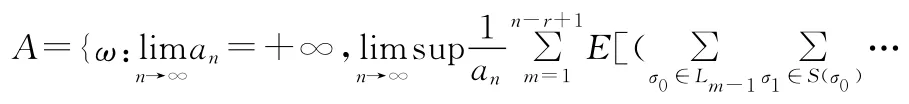
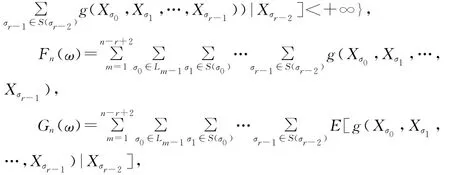
则

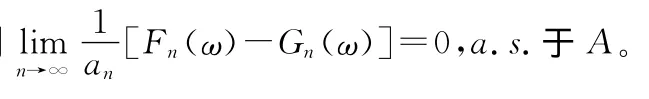
证明 对于m≥1，存在K＞0，满足

定理2 设｛Xσ，σ∈T｝是非齐次树T指标集马氏链，令

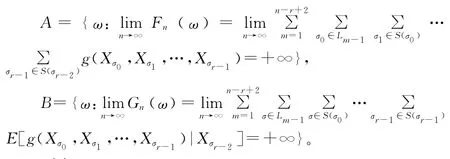
则有

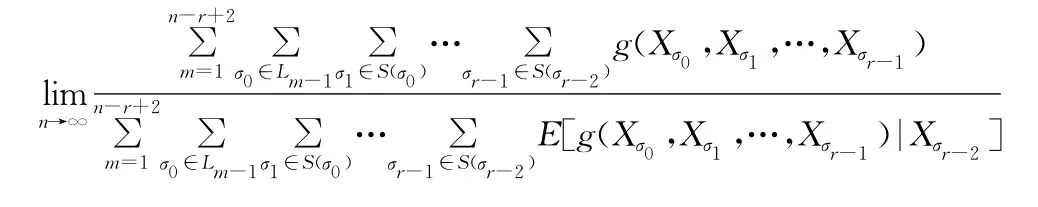
且A＝B a．s．于B。

证明 在定理1中，令an＝Gn（ω），则有，由定理知（1）式成立。

在定理1中，令an＝Fn（ω），则有

由（1）式有limGn（ω）＝1，ω∈A∩B，则有n→∞Fn（ω）

所以有A＝B a．s．

［1］ Benjamini I，Peres Y．Markov chains indexed by trees［J］．Ann Probab，1994，22：219－243．

［2］ Yang Weiguo．Some limit properties for Markov chains indexed by a homogeneous tree［J］．Stat．Letts．，2003，65：241－250．

［3］ Fan Zhenyao，Jin Shaohua，Bian jing．A new application of stochastic matrices［G］／／The Proceedings of 3International Workshop on Matrix Analysiss，Liverpool：World Academic Press，2009（1）：121－125．