时间序列预测模型的改进及应用——以预测甘肃省天水市的胆囊炎发病率为例

马亮亮

（攀枝花学院 数学与计算机学院，四川 攀枝花617000）

气象因素是影响甘肃省天水市胆囊炎发病率的一种非线性、多变量时间序列。对于非线性系统，一般采用基于非线性自回归移动平均模型进行预测，但很难为这种模型找到恰当的参数估计方法，因此传统的非线性系统的识别，在理论研究和实际应用方面均存在极大的困难［1－8］。为了有效利用各种时间序列预测模型的优点，克服单一模型的缺陷，一些学者基于著名的M－竞争理论提出了时间序列组合预测模型，而且实证结果表明，相对于单一模型，组合预测模型能够较大程度地利用预测样本的各种信息，大幅度地提高时间序列的预测精度，比单一模型考虑的问题更系统、更全面［9－10］。

为了提高时间序列的预测精度，文中考虑了时间序列的环境影响因子，将主成分分析（Principal Components Analysis，PCA）和最小二乘支持向量机（LSSVM）相融合，给出了一种新的时间序列组合预测模型（PCA－LSSVM），并通过甘肃省天水市胆囊炎发病率对此模型预测性能进行验证。

1 模型基本理论简介

1.1 主成分分析方法

主成分分析是考察多个变量间相关性的一种多元统计方法。它的基本思想是通过降维过程，将多个相互关联的数值指标转化为少数几个互不相关的综合指标，即用较少的指标来代替和综合反映原来较多的信息，这些综合后的指标就是原来多指标的主要成分［11－12］。

假设有n个样本，每个样本测得p项指标（p＜n）。当p个指标之间存在相关关系时，可以通过线性变换方法找到一组新指标z1，z2，…，zm，且它们满足下列条件：

（1）各zi是原指标的线性函数，且它们相互垂直；

（2）各zi之间相互独立；

（3）这些zi提供原指标所含有的全部信息，且z1提供的信息量最多，z2次之，…，zm最少；

其中zi为原指标x1，x2，…，xp的第i主成分（i＝1，2，…，p）。

设x＝（x1，x2，…，xp）是一个p维随机向量，且E（x）＝μ，协方差D（x）＝V。考虑它的线性变换：

则有：

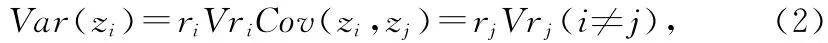
如果z1＝r1′x 满足：（1）r1′r1＝1；（2）Var（z1）＝Mar

r′r＝1Var（r′x），则称z1是在x的所有线性组合中最能综合p个变量信息的一个特殊的线性组合。如果一个主成分不足以代表p个变量所包含的信息，就考虑z2。为了能有效地代表原变量的信息，z1已有的信息在z2中不再出现，即满足Cov（z1，z2）＝0，类似可求z2以及其它的主成分。

主成分分析的目的是为了减少变量的个数，故一般不用p个主成分，而用m＜p个主成分。m的选取则要看累计贡献率［13－14］。

1.2 最小二乘支持向量机算法（LSSVM）

SVM是对一个凸二次规划进行求解，所得的解唯一且最优，不存在像神经网络的局部最优问题，但当训练样本较大时，所需计算资源很大。最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）是SVM的一种变体，它将问题转化成对一个线性方程求解，所需计算资源少，具有较高的准确率［15－19］。由于本文主要进行回归预测，因此只介绍LSSVM的回归算法。

给定样本数据为（x1，y1），…，（xm，ym），xi∈Rk表示输入向量，yi∈Rk表示输出向量，f（x）为待估计的未知函数，进行非线性映射：

式中H为特征空间。那么被估计函数f（x）可以表示为

因此，LSSVM回归问题可以表示为

式中ei∈Rk为误差变量，i＝1，2，…，m。

2 PCA－LSSVM模型预测原理

PCA－LSSVM模型的预测原理为：首先利用PCA对时间序列的影响因子进行筛选降维，只保留对系统影响较大的变量，然后采用LSSVM模型对保留变量进行建模和预测。PCA－LSSVM具体的预测流程如图1所示。

图1 PCA－LSSVM模型的预测流程

3 评价指标和参比模型

为了评价PCA－LSSVM模型性能的优劣，选择PCAMLR，ARIMA，LSSVM 作为参比模型，其中PCA－MLR表示先采用PCA进行影响因子筛选，然后再采用多元线性回归（Multiple Linear Regression，MLR）进行建模和预测；ARIMA表示直接采用ARIMA模型进行建模和预测；LSSVM表示直接采用LSSVM模型进行建模和预测，并使用均方误差（Mean Square Error，MSE）和平均相对误差（Mean Absolute Percentage Error，MAPE）作为模型的评价指标。MSE和MAPE分别定义为

其中yi表示时间序列的实际值，yi表示模型的预测值，n表示测试样本数。

4 实证研究

4.1 数据来源

数据资料来源于甘肃省天水市疾病预防控制中心提供的2000年1月至2005年12月胆囊炎发病率（y）。胆囊炎发病率的气象影响因子有：月平均气压x1（pha），月平均气温x2（℃），月平均相对湿度x3（%），月平均风速x4（m／s），月降水量x5（mm）。

4.2 主成分分析（PCA）

利用气象影响因子月平均气压x1，月平均气温x2，月平均相对湿度x3，月平均风速x4，月降水量x5作主成分分析，得特征根和主成分贡献率，如表1所示。

表1 主成分统计分析

从主成分分析结果可知，第一主成分的特征根为2．598，它解释了总变异的51．969%；第二主成分的特征根为1．539，它解释了总变异的30．771%。前两个特征根均大于1，累计贡献率82．740%。为了得到一个可靠的预测模型，需要从众多影响因子中挑选出对胆囊炎发病率变化贡献率大的影响因子。由于第3个主成分的特征根较接近于1，故宜取前3个主成分，此时累计贡献率达94．586%，即采用前3个主成分（z1，z2，z3）代替原有的5个变量（x1，x2，x3，x4，x5）进行建模和预测。

前3个主成分与各个变量 x1，x2，x3，x4，x5的 关 系如下：

其中stdxi（i＝1，2，3，4，5）表示标准指标变量：

4.3 结果与分析

4.3.1 MLR拟合

运用PCA筛选的对胆囊炎发病率影响显著的前3个主成分z1，z2，z3，采用 MLR进行预测，借助于SPSS11．5实现，得到的线性回归方程为：

将式（8）至式（10）的z1，z2，z3表达式代入式（16），得到因变量y与标准自变量stdx1，…，stdx5的线性回归方程：

将标准自变量还原为原自变量，得到因变量y与原自变量x1至x5的线性回归方程为：

模型主要参数为：相关系数R＝0．924；F＝1．579；显著水平p＝0．0421＜0．05，表明建立的线性方程达到显著性要求，该方程可以进行预测应用。

4.3.2 ARIMA拟合

利用胆囊炎发病率（y）绘制该序列的样本自相关分析图（图2），可知p＝1，d＝1，q＝2，此时 ARIMA（1，1，2）模型对应的方程为：

式中随机项εt是相互独立的白噪声序列，且服从均值为0，方差为σ2的正态分布；B为后移算子。

图2 胆囊炎发病率序列样本自相关分析图

4.3.3 LSSVM 拟合

一般情况下，w可能为无限维，对式（4）直接进行求解相当困难，因此通过引入拉格朗日乘子将该问题转化为对偶问题进行求解，于是有

通过求L对w，b，ei，αi的偏导数等于0的解，可得到最优解的约束条件为

与SVM的最优条件相比，只有αi＝rei不同，因此αi＝rei使LSSVM不再具有SVM所具有的稀疏性。利用式（20）消去w与ei得到式（4）的解方程为

式中向量lm＝（l，l，…，l）T，α＝（α1，α2，…，αm），Y＝（y1，y2，…，ym），Ω 为矩阵，其定义为 Ω＝φ（xi）Tφ（xj），i，j＝1，2，…，m。

通过式（21）转换成为线性方程组，并求式（21）就可以求得α与b的值，于是得到被估计函数的表达式，即式（4）变为

4.3.4 PCA－LSSVM 拟合

运用经过PCA筛选的3个主成分z1，z2，z3建立LSSVM模型，再采用GA算法对模型参数进行优化。

4．5 几种模型拟合和预测结果对比

将胆囊炎发病率数据分成两部分：2000年1月至2004年12月的数据作为训练集，2005年1月至12月的数据作为测试集，以便获得实际胆囊炎发病率建模精度与拟合能力、预测能力的评定。

拟合后各模型的MSE（均方误差）和MAPE（平均相对误差）如表2所示。

表2 各模型的拟合性能比较

从表2的对比结果可知，在所有模型中，PCA－LSSVM模型拟合精度最高，误差最小，表明，采用PCA对胆囊炎发病率的影响因子进行主成分分析，然后采用LSSVM进行建模，能更加准确描述胆囊炎发病率的变化规律，有效提高胆囊炎发病率的拟合精度。

由于评价一个预测模型的好坏，主要考察其预测能力而非回代拟合结果，因此，再分别采用PCA－MLR，ARIMA，LSSVM，PCA－LSSVM模型进行独立预测，预测结果如表3所示。

表3 几种模型对2005年胆囊炎发病率的预测结果 %

从表3可知，线性MLR模型、ARIMA模型和LSSVM模型的预测效果较差，主要是因为它们均只能反映胆囊炎发病率的片段信息，不能全面捕捉到胆囊炎发病率的动态变化规律；而组合预测模型PCA－LSSVM与这些模型相比，预测精度较高。这是由于组合预测模型能够充分利用时间序列数据中的信息，并对胆囊炎发病率变化规律进行深入挖掘，避免了单一模型的局限性，其预测结果才有了较为明显的提高。同时，由表2可知，PCA－LSSVM的MSE和MAPE 值小于PCA－MLR，ARIMA和LSSVM的相应值。这是由于PCA－LSSVM模型的预测算法采用LSSVM，而LSSVM是一种基于结构风险最小准则的机器学习方法，对于小样本、非线性系统其泛化能力比MLR和ARIMA更强，因此预测结果与实际情况更加吻合，从而可获得比PCA－MLR，ARIMA更高的预测精度。对比结果表明PCA－LSSVM为胆囊炎发病率的最佳预测模型。

5 结术语

时间序列受到众多因子的影响，呈现高度非线性变化规律，难以建立精确的数学模型，利用LSSVM模型本身的优点，将PCA引入到时间序列建模中，建立了一种时间序列组合模型（PCA－LSSVM模型），并应用于胆囊炎的预测中。实例结果表明，PCA－LSSVM模型简单、容易实现，提高了胆囊炎发病率预测准确率，较好地揭示了胆囊炎发病率的变化规律。

［1］ 马亮亮，田富鹏．基于非对称ARCH模型的海西州地区胆结石发病情况研究［J］．科技导报，2009，27（24）：51－55．

［2］ 马亮亮，田富鹏．ARMA模型在胆结石发病率预测中的应用［J］．军事医学科学院院刊，2010，34（5）：1－4．

［3］ 马亮亮，田富鹏．时间序列分析方法在胆囊炎发病率预测中的应用［J］．中华实验外科杂志，2010，27（6）：779．

［4］ 马亮亮，田富鹏．不同时间序列分析方法在胆结石发病率预测中的应用［J］．中国老年学杂志，2010，30（13）：1777－1780．

［5］ 向昌盛．基于支持向量机的时间序列组合预测模型［D］．长沙：湖南农业大学，2011：23－32．

［6］ 马亮亮．基于非线性分类和回归问题中的支持向量机算法［J］．天水师范学院学报，2009，29（5）：44－47．

［7］ 黄东远，陈晓云．一种新的支持向量回归机的模型选择方法［J］．福州大学学报：自然科学版，2011，39（4）：527－532．

［8］ 邓乃扬，田英杰．数据挖掘中的新方法——支持向量机［M］．北京：科学出版社，2004．

［9］ 马亮亮，田富鹏．基于因子RBF神经网络预测模型的脑梗塞发病率预测［J］．统计与决策，2010（10）：200－201．

［10］ 马亮亮，田富鹏．基于人工神经网络的非稳态心肌病发病率预测模型研究［J］．中国老年学杂志，2011，31（24）：4877－4878．

［11］ 罗盛健．基于人工神经网络的刚竹毒蛾发生面积的预测模型［J］．华东昆虫学报，2006，15（1）：37－39．

［12］ Salgdo R M，Pereira J J F，Ohishi T，et al．A hybrid ensemble model applied to the short－term load forecasting problem［C］．Vancouver：International Joint Conference on Neural Networks，2006：2627－2634．

［13］ Vila J P，Wagner V，Neveu P．Bayesian nonlinear model selection and neural network：A conjugate prior approach［J］．IEEE Trans on Neural Networks，2000，11（2）：265－278．

［14］ 向东进．实用多元统计分析［M］．武汉：中国地质大学出版社，2005：120－184．

［15］ 朱建平，殷瑞飞．SPSS在统计分析中的应用［M］．北京：清华大学出版社，2007：171－178．

［16］ 马亮亮，田富鹏．主成分分析与因子分析在肺心病发病情况分析中的应用［J］．四川文理学院学报，2010，20（2）：65－69．

［17］ 马亮亮，田富鹏．基于糖尿病相关因素的主成分分析［J］．长春大学学报，2009，19（4）：61－63．

［18］ Dong J X，Krzyzak A，Suen C Y．An improved handwritten Chinese character recognition system using support vector machine［J］．Pattern Recognition Letters，2005，26（12）：1849－1856．

［19］ Wan V，Renals S．Speaker verification using sequence discriminate support vector machines［J］．IEEE Transactions on Speech and Audio Processing，2005，13（2）：203－210．