一类斑块环境中的捕食－食饵模型动力学分析

孟 超，周玉元，王闯华

（湖南农业大学 理学院，长沙410128）

0 引言

对斑块环境中生态动力系统性质的研究是数学生态学的一个热点问题。许多学者对斑块环境中生态动力系统的持久性、稳定性与周期性做了大量的研究，但对各种群占有的斑块数量变化规律的研究很少。1994年，Vincent A．Jansen研究了一类斑块环境中三营养食物链模型分别在只有食饵扩散和只有捕食者扩散的情况下平衡点的存在性、稳定性［1］，2008年，Duan Hui－ling研究了斑块环境中的三营养 模型的平衡点的存在性、稳定性［2］。

本文在文献［2］的基础上提出了一类斑块环境下具HollingII型功能反应函数的捕食－食饵模型：

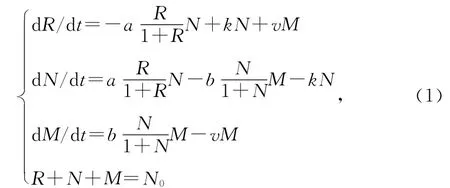
其中R表示空资源斑块的数量，N表示被食饵种群占领的资源斑块数量，M表示被食饵和捕食者同时占领的斑块数量，总资源斑块数量为N0（N0＞1），且有R＋N＋M＝N0，a＞0，b＞0，k＞0，v＞0。

本文中研究平衡点的全局稳定性，需用到如下引理。

1 主要结论

1.1 系统平衡点

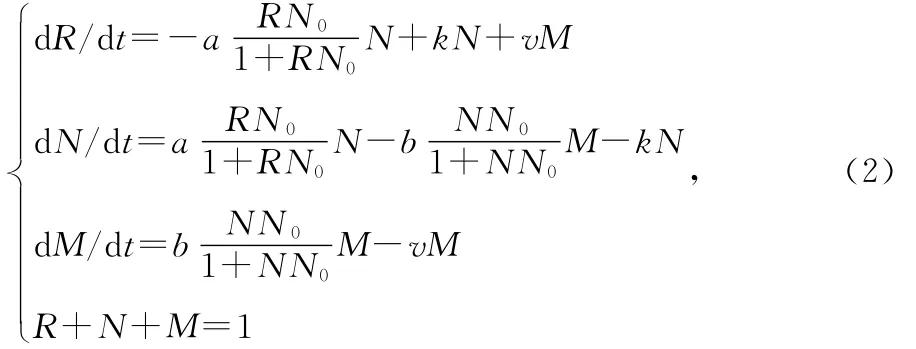
其中a＞0，b＞0，k＞0，v＞0。

通过计算可得系统（2）的3个平衡点：

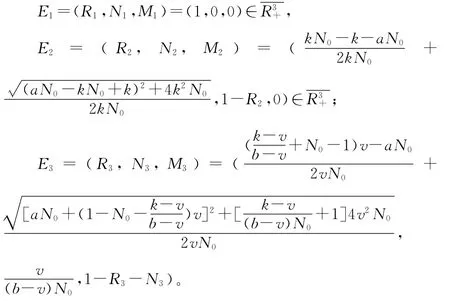
1.2 平衡点的稳定性

为研究平衡点稳定性，将R＝1－N－M代入（2），得

成本问题是高校后勤保障服务的核心问题，也是最敏感的问题之一。要明确政府、学校、服务实体在承担高校公益性服务中的责任，建立健全高校公益性服务的成本补偿机制和经营性服务的价格形成机制，发挥政府在高校公益性服务项目中的主体作用。对高校公益性服务项目，由政府明确税收优惠和经济补偿政策。根据政策，各级政府要对高校进行相应的资金投入，以减轻高校和服务实体的成本负担，为师生提供更优质的后勤保障服务。

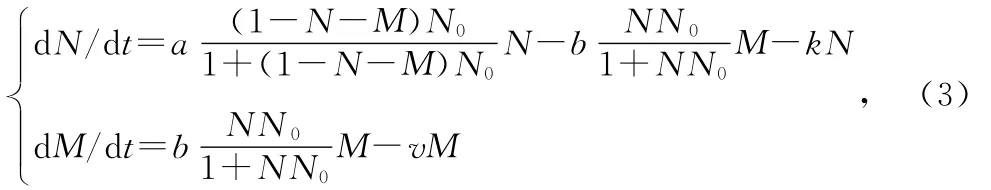
则系统（2）的平衡点就转化为系统（3）中对应的平衡点

E＊1＝（N1，M1）＝（0，0），E＊2＝（N2，M2）＝（1－R2，0），E＊3＝（N3，M3）＝（，1－R3－N3）。

其中R2＝，R3＝（＋

由前面所述可知仅在S2＝｛（N，M）｜0＜N＜1，0＜M＜1，0＜N＋M＜1｝内讨论，并记＝｛（N，M）｜0≤N≤1，0≤M≤1，0≤N＋M≤1｝。

证明 ① 在点E＊1处，易得系统（3）雅可比矩阵的特征值为，当aN0＜k时，从而E＊1是系统（3）稳定的奇点。

在点E＊2＝（N2，M2）＝（1－R2，0）处，通过计算可得系统（3）雅可比矩阵的特征值，，由定理条件显然有λ1＜0，λ2＜0，因此E＊2是系统（3）稳定的奇点。

② 参照①中E＊1的证明方法易知E＊1是系统（3）稳定的奇点；

③ 参照①中E＊1，E＊2的证明方法，易知E＊1，E＊2均为系统（3）稳定的奇点。

证明 由定理1知，当满足定理2条件时，E＊3是局部渐近稳定的。取Dulac函数［3］B（N，M）＝eMM－3，分别用P，Q表示（3）式等号右边部分，即

通过计算对（N，M）∈S2，当满足定理2的条件时恒有

系统（3）在S2内不存在极限环，再结合定理1可知，系统（3）的正平衡点E＊3是全局渐进稳定的。

2 结语

本文通过分析系统雅可比矩阵特征值，得到了系统局部稳定的一个充分条件，在此基础上，运用Dulac判据，得到了保证其正平衡点全局稳定性的充分条件。

通过分析可知：若通过人为控制，如投放食物等，使得食饵种群对资源斑块的侵占率低于消耗率，捕食者种群对食饵斑块的侵占率高于消耗率，就可保证该生物系统处于稳定状态。

［1］ Vincent A A Jansen．Effects of dispersal in a tritrophic metapopulation model［J］．Mathematical Biology，1995，34（2）：195－224．

［2］ Duan Hui－ling．Dynamics of tri－trophic models in patch environment［J］．重庆三峡学院学报，2008，24（3）：64－67．

［3］ 王冲，刘壮，刘荣辉．Dulac函数在定性理论中的构造探讨［J］．齐齐哈尔大学学报，2011，27（4）：73－75．