基于PID控制的液压伺服非正弦振动系统设计
刘 涛,程相文,高军霞
(1.河北联合大学 机械工程学院,河北 唐山063009;2.唐山盾石电气有限责任公司,河北 唐山063000;3.唐山学院 机电工程系,河北 唐山063000)
0 引言
板坯连铸技术的核心部件是结晶器,尽管各种板坯连铸机所用的结晶器构造和形状不同,但在振动形式上却越来越趋于一致,即液压振动,属高频率、小振幅的非正弦曲线振动方式。[1]采用计算机控制的电液伺服结晶器振动装置可以很方便地产生各种振动,实现控制过程监督、实时显示,并根据拉坯速度实时修改振动参数[2],提高连铸坯质量和金属收得率,从而实现连铸过程的自动化。
某钢铁公司热轧带钢板坯连铸机结晶器系统原理如图1所示。液压振动系统主要由伺服阀、液压缸等组成,液压缸的管路以并联方式连接到液压站上,液压站用于提供液压动力,管路上还配有控制伺服阀的截止阀,由压力传感器检测油压,伺服阀中有位移传感器检测阀芯的位置。另外,结晶器左、右两边分别装设位移传感器,检测结晶器的实际位移。液压缸的动作以理想的频率、行程和波形造成结晶器的振动动作。
1 结晶器液压伺服振动系统静态设计
在设计中采用德马克公司开发的非正弦振动曲线,描述为

式中:A为结晶器振动振幅;f为结晶器振动频率;t为振动时间;h为非正弦振动曲线偏斜率。
参考实际生产工况,确定结晶器负载范围为0~4 500kg。液压伺服缸端非正弦振动参数设置为:A=6mm,f=4Hz,h=0.4。结晶器预设非正弦振动曲线如图2所示。
液压缸加速度变化规律为
非正弦振动加速度曲线如图3所示。由图可看出各条曲线连续而光滑,加速度控制在5.2m/s2以内,由此产生的冲击在系统允许范围内。
在连铸结晶器振动过程中,结晶器端总负载组成分为以下几部分:结晶器装置自身重量、负载惯性力以及振动过程中结晶器内壁与铸坯间的摩擦力,包括干摩擦和粘性摩擦,对结晶器振动端到液压缸端的负载折算,总负载FL的表达式为

图1 结晶器液压振动系统原理图

图2 非正弦与正弦位置曲线对比

图3 非正弦振动加速度曲线

式中Ff为结晶器内壁与铸坯表面的干摩擦力,这里取Ff=10 000N;m为负载质量;Bp为粘性阻尼系数;g为重力加速度。
根据对液压缸一个行程周期内的50个点采集负载力F(N)及负载速度v(m/s),利用 MATLAB软件绘制出液压缸v-F负载轨迹,如图4所示。最大功率点功率Nmax=15.1kW,此时负载力F*L=37 397.79N,负载振动速度V*L=0.404 6m/s。
以最大功率点为参照选择系统压力Ps=16MPa。为了使液压动力元件能与负载做到最佳匹配,取液压缸输出最大功率时的负载压力为PL*=23Ps,则液压缸面积为

图4 负载轨迹
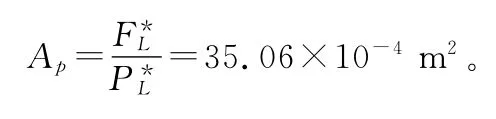

最大功率时所需的供油流量q*L=ApV*L=83.4L/min。
考虑泄漏等影响,将系统供油流量qL增大15%左右,取qL=1.15q*L=96L/min。
根据阀口总压降和所需供油流量,确定选择MOOG公司生产的电液伺服阀,型号规格为D661G45H。该阀在阀压降为1MPa时额定流量为45L/min,最大工作压力28MPa,额定电流20mA。
2 结晶器液压振动系统动态设计
伺服阀控液压缸的动态工作过程可用下面3个方程描述[3]:

式中:Kq为伺服阀流量增益;Kc为伺服阀流量系数;mt为负载质量;Bp为粘性阻尼系数;K为负载弹簧刚度;Ctp为液压缸总泄漏系数;Fg为外加干扰负载力。
由上式3个基本方程得到阀芯位移xv到液压缸输出位移xp的传递函数为

阀控缸输出位移xp对Fg的传递函数为
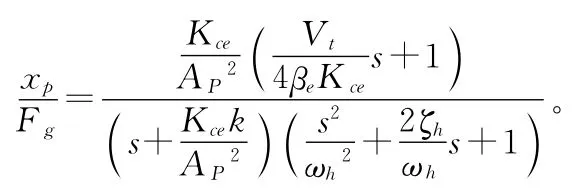
式中Kce=Kc+Ctp,指的是考虑泄漏因素后的总压力流量系数。
系统有效体积弹性模量βe=700MPa;液压缸有效面积34.34×10-4m2;液压缸活塞行程L=25mm,则液压缸最大容积Vt=LAp=8.59×10-5m3;动力元件的阻尼比一般根据实测确定,这里取ζh=0.2;忽略液压缸泄漏,总流量-压力系数Kce=Kc,由阀的零位泄漏决定,取Kce=3.73×10-12m3/(s·Pa)。
当电液伺服阀的频宽与液压动力元件的固有频率相近时,电液伺服阀的传递函数可以看成是二阶环节。设计的液压动力元件的固有频率
则液压动力元件的固有频率ω0=292rad/s。
查MOOGD661G45H伺服阀样本得出,伺服阀的固有频率ωsv=571.2rad/s,阻尼比ζsv=0.7。由于该阀在阀压降1MPa时额定流量为45L/min,因此其最大空载流量为

阀的额定电流为in=20mA=0.02A,则伺服阀的增益为。
电液伺服阀的传递函数为

伺服放大器、位移传感器的响应很快,因此一般忽略它们对系统的动态影响,看成比例环节,位移传感器的传递函数可表示为;伺服放大器的传递函数可以表示为。
结合以上分析,得出系统传递函数方块示意图如图5所示。

图5 系统传递函数方块图
3 仿真分析
为了对系统输出性能进行预估,利用如图6所示的系统方框图,采用MATLAB仿真软件对系统进行仿真[4]。仿真时代入有关数据,可直接得出系统在时域的输入、输出曲线,如图7所示。系统的输出基本能跟随输入信号的变化,但是存在幅值超调,振幅最大误差值为1×10-5m,位置控制精度达不到设计要求。

图6 仿真模型图

图7 输入、输出曲线
利用Simulink模块强大的功能,构建加入PID控制器后的仿真模型如图8所示。
不同PID控制参数下的伺服控制系统输入输出性能仿真曲线如图9-11所示。通过研究仿真曲线,以求确定最佳PID控制参数。
根据图9-11,综合考虑系统的响应速度与位置控制精度,确定最佳PID控制参数为Kp=1,Ki=1,Kd=0。
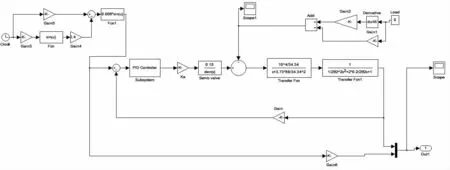
图8 加入PID控制器后的仿真模型(非正弦输入)

图9 仿真曲线(Kp=0.6,Ki=0.2,Kd=0)

图10 仿真曲线(Kp=0.6,Ki=1,Kd=0)

图11 仿真曲线(Kp=1,Ki=1,Kd=0)
4 结论
本文对结晶器的液压伺服非正弦振动系统的设计、仿真优化、控制等进行了详细地阐述说明,并利用 MATLAB/Simulink软件确定了最佳PID控制参数。仿真结果表明,在非正弦振动控制系统中增加PID控制器可大大改善系统的控制精度,本文可为类似带弹性负载的液压伺服非正弦振动设计和PID控制性能仿真分析提供借鉴和参考。
[1] 孔德才.结晶器振动系统在连铸中的应用与研究[J].连铸,2007(3):23-25.
[2] 吴晓明.板坯连铸结晶器液压伺服振动装置控制策略的研究[D].秦皇岛:燕山大学,2007.
[3] 高军霞,杨国权.基于 MATLAB/SIMULINK的篦式冷却机液压系统改造[J].液压与气动,2011(9):101-103.
[4] 高军霞,杨国权.房屋液压减震装置的设计与研究[J].机床与液压,2011,30(12):54-56.

