混合图像降噪技术研究

张银蒲

（唐山学院 信息工程系，河北 唐山063000）

图像传输是现代通信的重要内容之一，但是图像中常常不可避免地混杂着一定的噪声干扰，这些噪声又一定程度上影响着图像的质量，从而不利于图像的进一步分析和传输。评价图像质量好坏的性能指标有两个：一是图像逼真度，即被噪声污染的图像与原图像相比的近似度；一是图像读懂度，即通过被噪声干扰的图像而获取到的信息量。

对图像进行去噪处理可以进一步提高图像的质量，图像降噪的过程就是在抑制噪声和保留原始图像之间作权衡。因图像的非平稳性特性，在图像降噪技术中小波变换比傅立叶变换更有优势，所以在混合傅立叶——小波降噪算法中，一般是以小波变换为主，傅立叶变换技术为辅。

1 降噪算法原理

混合图像降噪技术原理［1］：（1）在傅立叶域中小幅度降噪，在原始图像扭曲较小的情况下，使噪声的水平降低。（2）在小波域中进一步去除在傅立叶域中未能清除的噪声。

在傅立叶域中进行维纳滤波器滤波，然后在小波域中，滤除掉傅立叶域中未能清除的有色噪声。混合图像降噪技术的核心，即研究有色噪声小波变换系数的特征。

1.1 小波变换系数［2］

由于小波是很多运算的近似特征函数，因此有色噪声的小波变换系数特点如下：（1）有色噪声在每一子带中的小波系数相关性很快消失。（2）小波系数在不同的子带之间相关性很小。

第二个特点还可以这样来解释：图像信号经时域向小波域的映射过程相当于通过了带通滤波器，不同子带中的小波系数与不同频率段的信号相对应，因此小波变换系数在不同子带之间的相关性很弱，有色噪声的小波变换系数，在每一个子带中几乎是白噪声。不同子带上的小波变换系数互不相关，而且噪声的方差也不同，因此可知，他们的互相关性很弱。以上结论不仅可以分析一维信号，也可以应用于二维信号分析。

1.2 混合图像降噪算法分析

假设含有噪声的图像为y，则

其中x为原始图像，n为高斯白噪声，且当高斯白噪声均值为零时，其方差为σn2。

而维纳滤波器是基于最小平均平方误差的滤波器，需事先知道原始图像以及噪声的功率谱密度。维纳滤波器在傅立叶变换域中进行降噪，传递函数为［1］：

2011年5月，天津农垦积极响应国家农业“走出去”号召，在保加利亚投资成立全资子公司——天津农垦集团保加利亚公司（以下简称“保加利亚公司”），主要从事国际贸易并租赁土地进行农产品种植项目。2014年1月，在习近平总书记“一带一路”倡议指引下，天津食品集团再次投资，以保加利亚公司收购100%股权的形式，接收了保加利亚一农场。农场拥有自有土地5.1万亩，租赁土地8.6万亩，以及与之配套的仓储、农机和运输设备。

其中，S（ω）为原始图像的功率谱密度，N（ω）为噪声的功率谱密度。假设干扰噪声是均值为零的高斯白噪声，因此其功率谱密度N（ω）为常数σn2。掺杂了噪声的图像y的傅立叶变换为Y（ω）。假设功率谱密度S（ω）在每一个频率点处的和邻近频率点处的相等，则对单个数据点Y（ω），可以在一个局部方形区域W（ω）上按下式估计S（ω）：

W（ω）作为方形窗口区域，傅立叶系数共M个，将x的最小功率谱密度设为a。为了原始图像不扭曲，则保守维纳滤波器公式如下［2］：

经傅立叶反变换，就可以得到傅立叶变换域中的滤波结果：

其中x′为不含噪声的图像，n′是未去除掉的有色噪声，x′的正交小波系数用X′（k）表示，z的小波变换系数可表示为［1］：

其中n′的小波系数为N′（k），因为 N′，N′（k）均为有色噪声，而N′（k）的自相关性会很快消失掉，同时在不同的子带之间，小波变换系数的相关性很小或基本不相关。在任何子带中，小波变换系数N′（k）基本为白噪声，其方差σn2可根据下式计算得出：

其中子带中位于k的小波函数为Ψk，有色噪声n′的自相关函数为r，这是｜H（ω）｜2σ2的傅立叶反变换，所以σ能够通过数值Ψ来计算得到。

假设小波系数X′（k）是方差为σ2（k）的独立高斯变量，并且相邻小波系数间方差的相关性很高，则可以构建线性最小均方误差估计器（Minimum Mean Square Error，简称MMSE），如下：

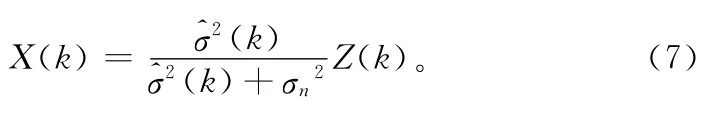
式中＾σ2（k）是σ2（k）的估计，则

由此可以总结出混合图像降噪技术的方法。

在傅立叶域中：1）估计原图像的功率谱密度可通过公式（3）来进行；2）降噪处理可通过应用公式（4）的维纳滤波器来进行。

在小波域中：1）σn2可通过表达式（6）在每一个子带中进行计算；2）应用公式（8）估计子＾σ2（k）；3）应用公式（7）估计＾X′（k）；4）重构降噪后的图像可以通过处理后的小波变换系数再进行小波反变换而得到。

实践中发现，在表达式（3）与表达式（4）中有两个参数a和b需要进行选择，对傅立叶变换域中7×7，小波变换域中3×3的窗口，选择a＝0．1σn2和b＝5能获得较好的效果，而且降噪效果对需要进行选择的两个参数的微小变化欠灵敏［1］。

2 实现混合图像降噪技术的流程

混合傅立叶－小波降噪技术需分别在傅立叶变换域和小波变换域对图像做相应处理。在傅立叶变换域中，为了不扭曲原始图像，先估计图像的功率谱密度，并通过维纳滤波器进行降噪，然后在小波域中，计算有色噪声在每一个子带中的方差，用处理后的小波变换系数通过小波反变换重构降噪后的图像。程序实现的流程图如图1。

图1 混合图像降噪技术流程图

3 混合图像降噪和傅立叶变换及小波变换降噪的对比分析

3.1 定性评价

通过对比来验证混合图像降噪技术是否有效。详见图2。

图2 不同降噪方法的效果图

图2（a）为原始图像，图2（b）为掺杂有色噪声图片，图2（c）为经过傅立叶变换降噪的图像，图2（d）为经过混合降噪后的图像。从图2中可对比得出，混合降噪效果要比单纯的傅立叶降噪效果好。混合图像降噪和小波图像降噪的对比如图3所示。

图3 混合图像降噪法和小波降噪法的对比

在这次图像处理中，用小波图像降噪方法对图像进行两次降噪，并和傅立叶－小波混合降噪图像进行对比。经分析得出，混合傅立叶－小波图像降噪的效果相比单独使用小波降噪法较好。

3.2 量化评价

峰值信噪比（Peak Signal to Noise Ratio，简称PSNR）是最为普遍和广泛使用的评价画面质量的客观量测方法。实践结果表明，峰值信噪比的大小与人眼观测到的视觉品质无法完全一致，存在峰值信噪比高的画面质量感觉比峰值信噪比较低者还差的现象。由于人眼的视觉对误差的敏感度并不是绝对的，使得视觉的感知结论与客观量测方法的结论不同。

通过定性评价可以用肉眼观察，混合傅立叶－小波降噪方法要优于单纯的傅立叶降噪或小波图像降噪。进一步量化地评价混合傅立叶－小波图像降噪的效果可通过对比图像的峰值信噪比来进行。

在上面的程序代码中，用out代表经过混合图像降噪后的图像，xF则为经傅立叶域变换降噪后的图像，X2为经过两次小波降噪处理后的图像，X为原始图像。通过计算，得出PSNR＝2536443，PSNR1＝23．1272，PSNR2＝20．8981。由于PSNR值越大，说明图像失真越少，所以量化评价上，混合傅立叶－小波图像降噪的效果要优于其他两种算法。

4 小结

通过使用小波技术对图像进行降噪，分别使用傅立叶变换和小波变换对图像进行处理，并针对两种算法的不同特性，提出了混合傅立叶——小波图像降噪的方法，这种算法综合了以上两种算法的优点，同时对降噪效果进行了定性和量化的评价，证明混合降噪方法有着较为理想的降噪效果。

［1］ 姜三平，郝晓剑．应用小波系数GSM统计模型的混合傅里叶－小波图像降噪［J］．2009，14（3）：448－451．

［2］ 姜三平．混合傅立叶－小波图像降噪及激光测速靶信号处理［D］．太原：中北大学，2008．