基于ANSYS数控铣削刀柄的模态分析

孙永吉 邹雪娟

(①兰州工业学院，甘肃兰州 730050;②中国石油兰州石化公司甘肃兰州 730060)

现代数控机床的设计趋于信息化、人性化、绿色化和数字化，机床的操作日趋简便。但大多设计者只将机床作为一个整体进行分析，而没有考虑机床装上刀柄系统后在加工中这个整体的性能，以及机床设计中选定的额定参数、丝杠螺距等在机床加工过程中产生的激励频率是否避开刀柄固有频率，这种机床应该选择哪种刀柄比较合理等因素。因为机床离不开刀柄系统，它不仅影响数控机床的生产效率，而且直接影响工件的加工质量，要根据刀柄的性能和特点来优化设计机床的结构，科学合理设计机床各项运动额定参数值，避免盲目追求速度而影响机床的使用性能。

1 常用刀柄的结构

现代数控铣床和加工中心使用的刀柄已标准化［1］，刀柄分为模块式和整体式。刀柄通过拉钉和主轴内的拉刀装置固定在机床主轴上，其作用是夹持刀具，传递速度和扭矩。刀柄与主轴孔的配合锥面一般采用7∶24的锥度，这种锥柄不自锁，换刀方便，与直柄相比有较高的定心精度和刚度。在我国应用最广泛的是整体式BT40和JT40刀柄，其结构如图1所示。

2 刀柄模型的建立

2.1 刀柄实体模型的建立

在建模时，针对刀柄的结构特点做了合理简化，刀柄尾部拉钉与刀柄的螺栓联接部分，联接螺栓和被联接件材料一样时，作为一体来处理。利用设计软件SolidWorks，按实际尺寸建立其结构模型，如图2所示。

2.2 有限元模型的建立

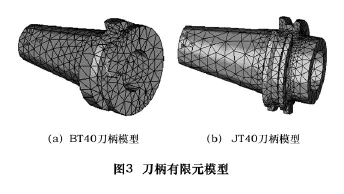
利用上述建立的三维实体模型，通过ANSYS与SolidWorks软件的接口，将模型导入 ANSYS中［2］，选择单元类型为Solid92，刀柄的材料为40Cr，其特性为:弹性模量E为2.06×1011Pa，泊松比μ为0.28，密度ρ为7 850 kg/m3。有限元模型如图3所示。

3 模态分析理论方程的建立

模态分析用于确定设计机构或机器部件的振动特性［3－4］，即结构的固有频率和振型，它们是承受动载荷结构设计中的重要参数。对于一个N自由度线性定常系统，其基本振动方程可写为:

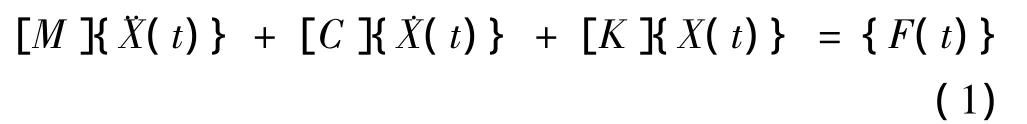
式中:［M］、［C］和［K］分别为弹性系统的质量矩阵、阻尼矩阵和刚度矩阵;{¨X(t)}、{˙X(t)}、{X(t)}分别为加速度向量、速度向量和位移向量;{F(t)}为动激励载荷向量。在进行模态分析时，因结构阻尼较小，对固有频率和振型影响甚微，故通常忽略不计。在这种情况下，分析结构的固有频率与振型问题转化为求解特征值与特征向量问题。对于无阻尼的自由振动，其动力学方程为:

任何弹性体的自由振动都可以分解为一系列简谐振动的叠加。上述方程有如下的简谐振动解:

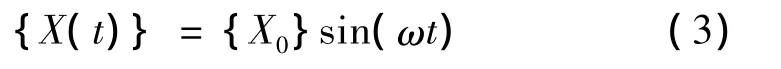
将式(3)代入式(2)得:

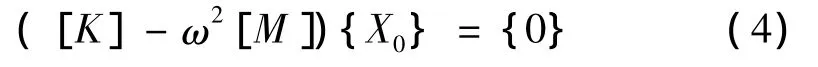
自由振动时，结构中各节点的振幅{X0}不全为零，所以式(4)中{X0}的系数矩阵行列式的值必须为零:

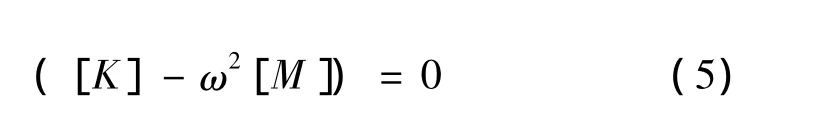
结构的刚度矩阵［K］和质量矩阵［M］都是n阶方阵，n是节点自由度数目，所以式(5)是关于ω2的n次方程，可以求出结构的n个固有频率，对每个固有频率，可以根据式(5)确定各节点的振幅值{X0}，称为结构的振型。

4 模态分析结果

为较全面地了解刀柄的动态特性，设定刀柄的额定角速度为8 000 r/min，铣床在铣削加工时振源频率属低频范围，刀柄指定模态提取数为4，模态扩展数为4，利用Lanczos法进行模态提取，得到BT40前4阶固有频率及振型如图4所示，JT40刀柄前4阶固有频率及振型如图5所示，两种刀柄计算结果如表1所示。

在实际应用中，以华中XK714数控铣床为例来说明，其机床整机前10阶固有振动频率如表2所示。

从表1和表2数据可看出，BT40刀柄前3阶固有频率均在机床前10阶固有频率范围内，且BT40刀柄1阶固有频率266.2 Hz和机床5阶固有频率262.96Hz接近，BT40刀柄3阶固有频率437.3 Hz和机床10阶固有频率438.54 Hz接近;JT40刀柄前2阶固有频率均在机床前10阶固有频率范围内，JT40刀柄381.8 Hz和机床9阶固有频率384.30 Hz接近。

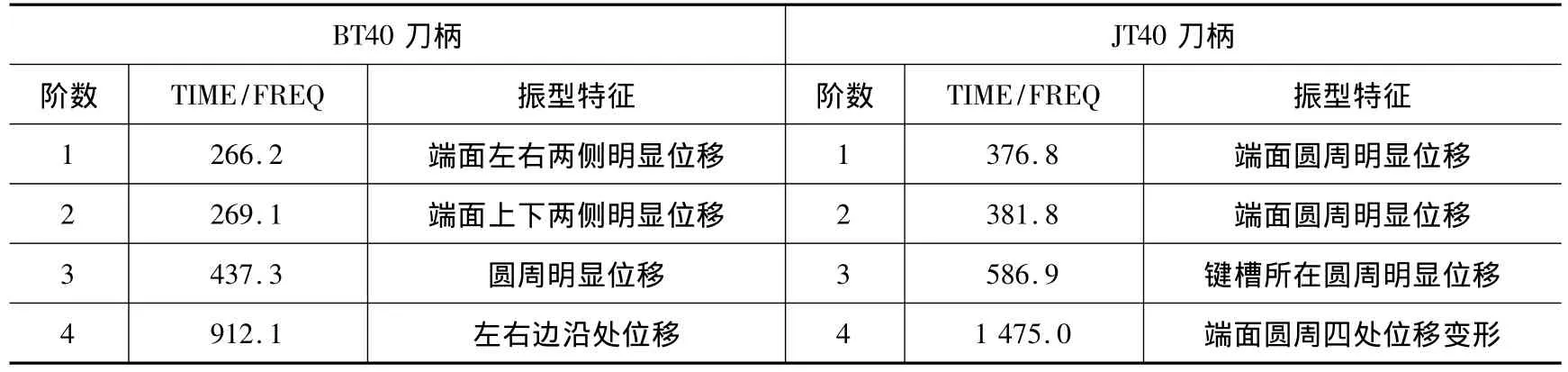
表1 刀柄计算结果 Hz

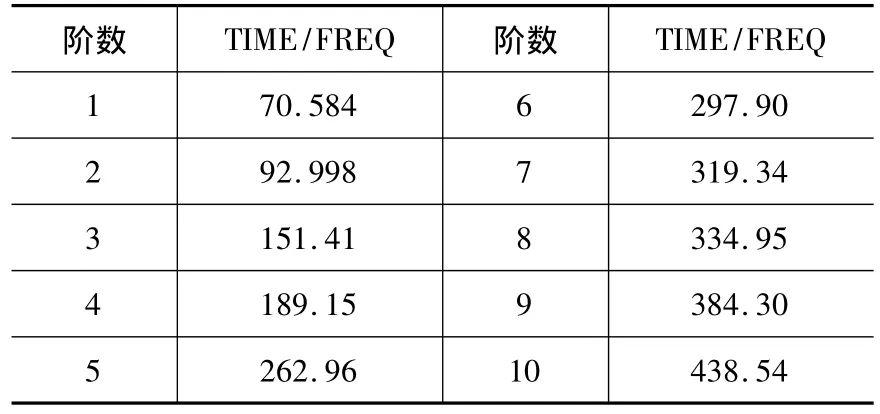
表2 XK714数控铣床前10阶固有振动频率 Hz

从上述数据比对可知，刀柄固有频率和机床固有频率接近易产生共振，故需要对机床进行优化来避开刀柄固有频率，或该机床在主轴结构设计中应选择JT40刀柄结构易避开机床固有频率。

在实用中，除高速切削机床(配备专门高速刀柄HSK)外，一般数控铣床的主轴额定转速不超过8 000 r/min，其产生的最大激励频率为8 000/60=133.3 Hz，根据表1可知BT40和JT40刀柄的固有频率均远远大于激励频率，故不会产生共振。

常用数控铣床的X/Y/Z进给速度最大为80 m/min，丝杠螺距为5 mm，其产生的最大激励频率为80×1 000/60/5=266.667 Hz，根据表1可知BT40刀柄1、2阶固有频率和该激励频率接近，若选择BT40刀柄易产生共振，根据分析结果该机床应设计成配备JT40刀柄的主轴结构形式。

5 结语

本文基于ANSYS软件对生产中常用的BT40和JT40两种整体式刀柄进行了分析，得出了其结构相关模态参数，其价值如下:

(1)为机床厂家对数控铣削机床的主轴结构设计、主轴额定转速设计、X/Y/Z三向最大进给速度设计、丝杠螺距选择、刀柄配备形式等提供重要依据，促使现代数控机床的设计更加完善合理，提升机床的综合切削性能。

(2)为操作人员选择切削用量提供一个考虑因素，避免选择的主轴转速、进给速度等参数产生的激励频率和刀柄固有频率接近，最大限度地发挥机床的切削性能，提高加工效率。

［1］林朝平，郭国林.数控机床刀柄系统的选择［J］.工具技术，2005，39(11):86－87.

［2］张朝晖.ANSYS8.0结构分析及实例解析［M］.北京:机械工业出版社，2005.

［3］刘延柱，陈文良，陈立群，等.振动力学［M］.北京:高等教育出版社，1998.

［4］贾启芬.机械与结构振动［M］.天津:天津大学出版社，2006.