磁悬浮永磁直线电动机非脆弱鲁棒H∞控制器设计**1

蓝益鹏 贺 伟

(沈阳工业大学电气工程学院，辽宁沈阳 110870)

由于磁悬浮永磁直线同步电动机兼有永磁电动机和直线电动机的双重优点，并具有非接触 、无摩擦、无磨损、环保等特点，省掉了机械传动机构，以零传动方式，极大地提高了进给系统的快速反应能力的运动精度，直线磁悬浮驱动技术在数控机床领域中存在着广泛的应用空间［1－2］。

针对控制对象的不确定性，鲁棒H∞控制作为较为成熟的方法，对抑制扰动具有良好的效果。随着求解凸优化问题的内点法的提出，LMI受到越来越多的关注，许多控制问题可以转化成一个LMI系统的可行性问题［3－5］。由于鲁棒控制器在实现中不可避免存在不确定因素，即控制器参数不可能精确实现，控制器本身参数也可能发生变化，由此可能导致闭环系统的性能下降，甚至稳定性遭到破坏，这就是控制器的脆弱性［6］。研究表明，对常规的鲁棒控制器而言，不管是用H∞，还是μ综合方法，都有可能出现控制器脆弱问题［7］。这样控制器在实际应用中对于对象和干扰的不确定性是鲁棒的，但本身却是脆弱的，不可靠的。

根据磁悬浮永磁直线电动机线性数学模型，利用LMI理论提出一种简化的非脆弱鲁棒控制器设计方法来求解控制器在参数摄动下的鲁棒H∞控制问题。

1 磁悬浮永磁直线同步电动机状态空间模型

磁悬浮永磁直线电动机的动子上有两套电气上相互独立的绕组，一套绕组是用于产生电磁推力的推力绕组，另一套绕组是用于调节磁悬浮力的悬浮绕组，专门用于对气隙磁场进行调节，从而改变磁拉力的大小，使永磁直线电动机靠自身产生的磁悬浮力来运行。使数控机床进给平台在直接驱动的同时能够从根本上消除摩擦，实现无摩擦进给［8］。

推力绕组中通入三相对称的正弦交流电流，采用id=0的控制策略，使推力绕组产生最大推力。在悬浮绕组中通入三相对称的正弦交流电流，采用iq=0的控制策略，以使悬浮绕组产生可控悬浮力。

假定d、q轴电感Ld=Lq=L。此时动子的电磁推力表达式为

磁悬浮永磁直线电动机的动子处于悬浮状态，与导轨之间无摩擦，其机械运动方程为［9］

式中:Fl为负载阻力;G为动子质量;Fd为端部效应力;Kf为电磁推力系数;v为动子线速度。由分析和实验得到端部效应力简化数学模型为

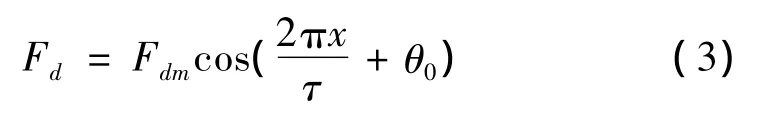
式中:Fdm为端部效应力波动的幅值;τ为极距;x为动子的直线位移;θ0为与直线电动机、定子电磁结构有关的常数。

在此情况下，磁悬浮永磁直线同步电动机的数学模型可描述为

其中:uq、iq分别为q轴动子电压和电流;ψf为永磁体基波励磁磁链;Rs为动子电阻;np为极对数。

2 非脆弱H∞鲁棒控制器设计和H∞性能分析

2.1 非脆弱H∞鲁棒控制器设计

用H∞控制理论设计控制系统，不论是鲁棒稳定还是干扰抑制问题，都可以归结为求解反馈控制器，使闭环系统稳定，并且从扰动输入w到被调输出z的闭环传递函数阵的H∞范数最小或者小于某一给定值［10］。

为此，将以上的线性系统控制归结为标准的H∞控制问题，考虑广义被控对象的状态空间实现为

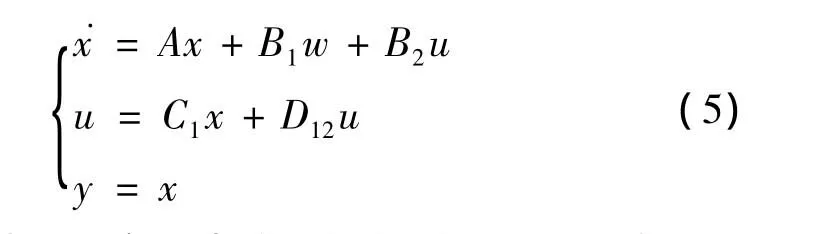
引理1:对于任意适当维数的矩阵M，N，E和FTF≤I的F，满足下列不等式:对任意实数ε≥0，

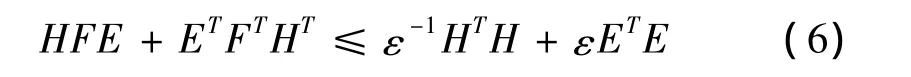
引理2:设A、X、Y、F为适维矩阵且‖F‖≤1，如存在 ε＞0，使得(I－εDDT)＞0，则:

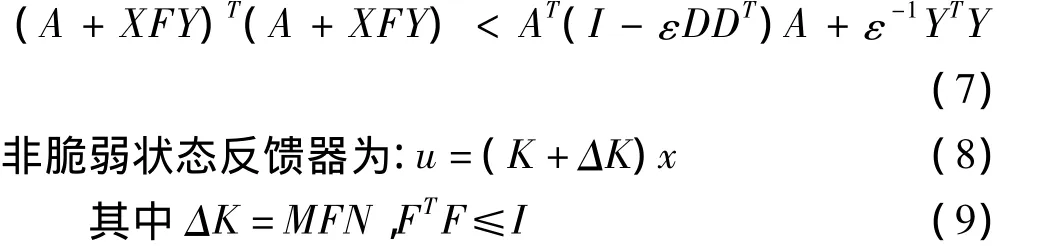
则相应的闭环系统为

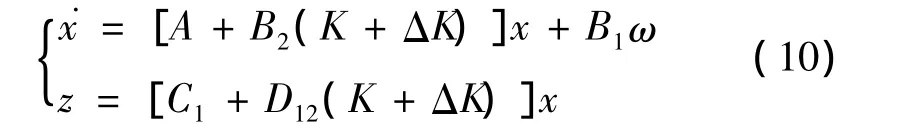
是渐近稳定的，且外界干扰ω到可控输出z的闭环传递函数满足以下不等式:

定理1假设干扰输入作用为零，如果存在对称矩阵P和矩阵M、N满足下列不等式:

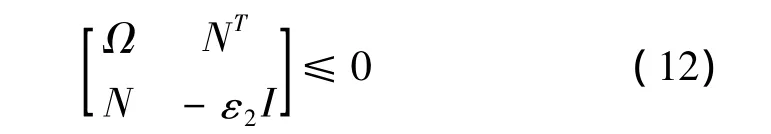
则系统式(10)在式(8)作用下是渐近稳定的。式中:Ω =P(A+B2K)T+(A+B2K)TP+ε1－1PB2M(B2M)TP

证明:构造如下的Lyapunov函数，P为正定对称矩阵，对V(X(t))求导同时考虑引理1得:V(X(t))=X(t)TPX(t)

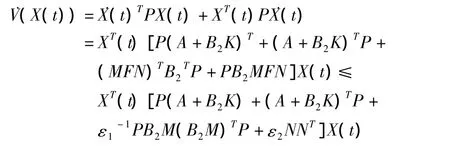
利用Schur补引理将上式进行矩阵分解，并且根据定理1可以得到V(t)＜0。

因此系统式(10)在状态反馈器式(8)的作用下是渐近稳定的。

2.2 H∞性能分析

定理2如果存在常数γ＞0，存在正定对称矩阵X和矩阵M，N，Y满足下列不等式:其中:X=P－1，Y=KP－1。

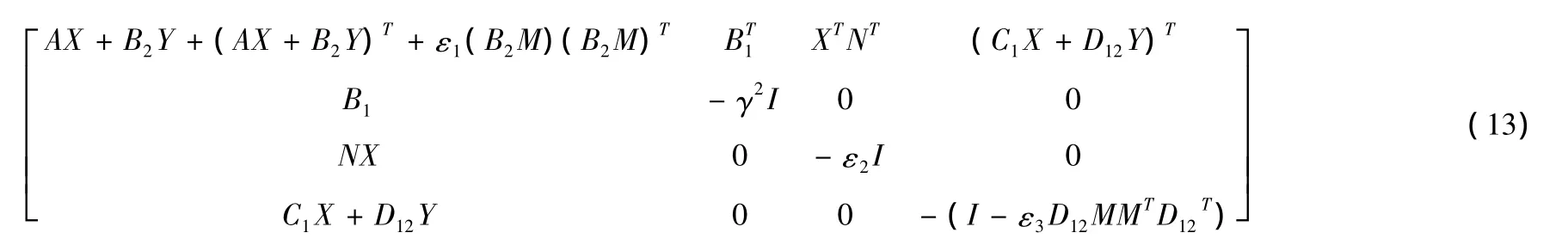
则被控输出Z(t)满足H∞性能约束:‖Z(t)‖2≤γ2‖ω(t)‖2

进而控制器:K=YX－1

证明考虑如下性能指标:

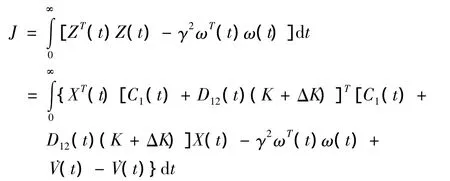
由引理2可得:

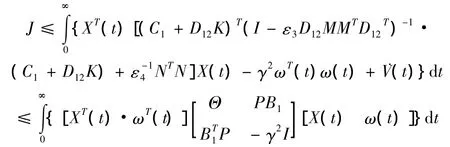
式中

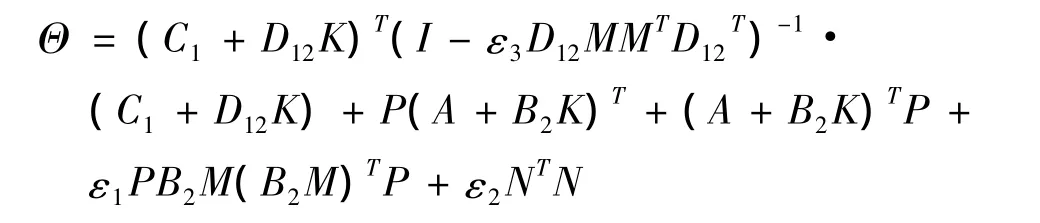
由Schur补引理将矩阵不等式分解，并且左右两端同时乘以 diag(P－1，P－1，I，I，I)得到式(13)。

根据定理2得到:J≤0

3 仿真研究

系统的额定参数如下:

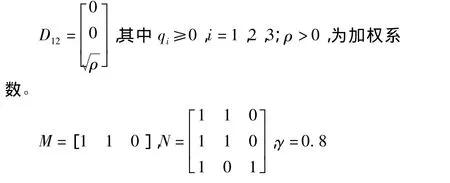
常规鲁棒控制器为

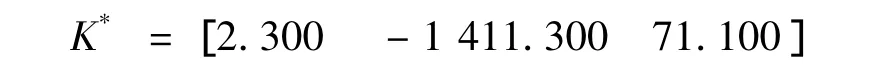
用MATLAB的LMI工具箱求得:

则非脆弱鲁棒H∞控制器为

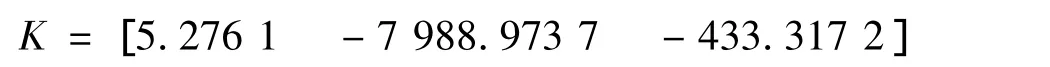
通过对系统进行仿真，在有扰动信号为阶跃信号情况下分别对状态变量:电流iq，速度v，位移s进行跟踪。t=0.6 s时突加载幅值为F=25 N的负载扰动，在t=0.7 s卸去扰动，

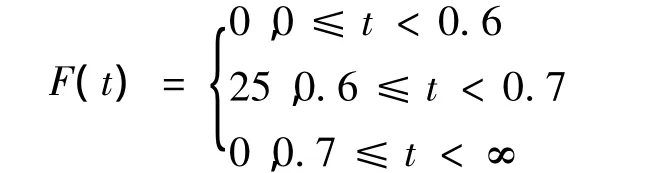
取3种满足式(9)增益摄动形式的F矩阵分别为

所分别对应的增益摄动为:

ΔK1=［1.1 0.6 0.5］(图 1 ～3 中曲线2 为有ΔK1增益摄动)

ΔK2=［2.3 1.2 1.1］(图 1 ～3 中曲线 3 为有ΔK2增益摄动)

ΔK3=［5.4 3.6 1.8］(图1 ～3中曲线4 为有ΔK3增益摄动)

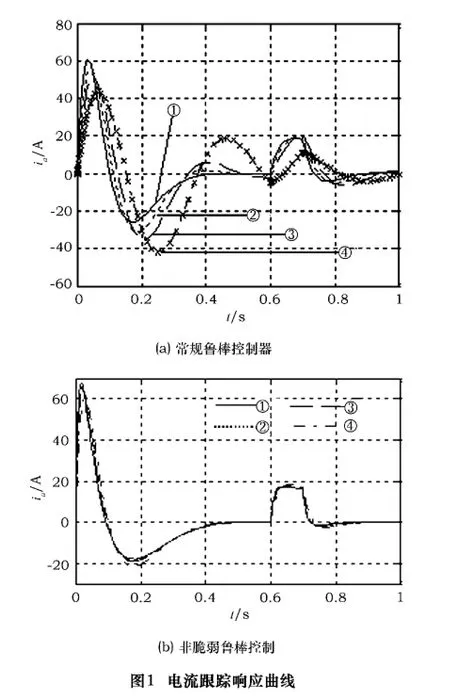
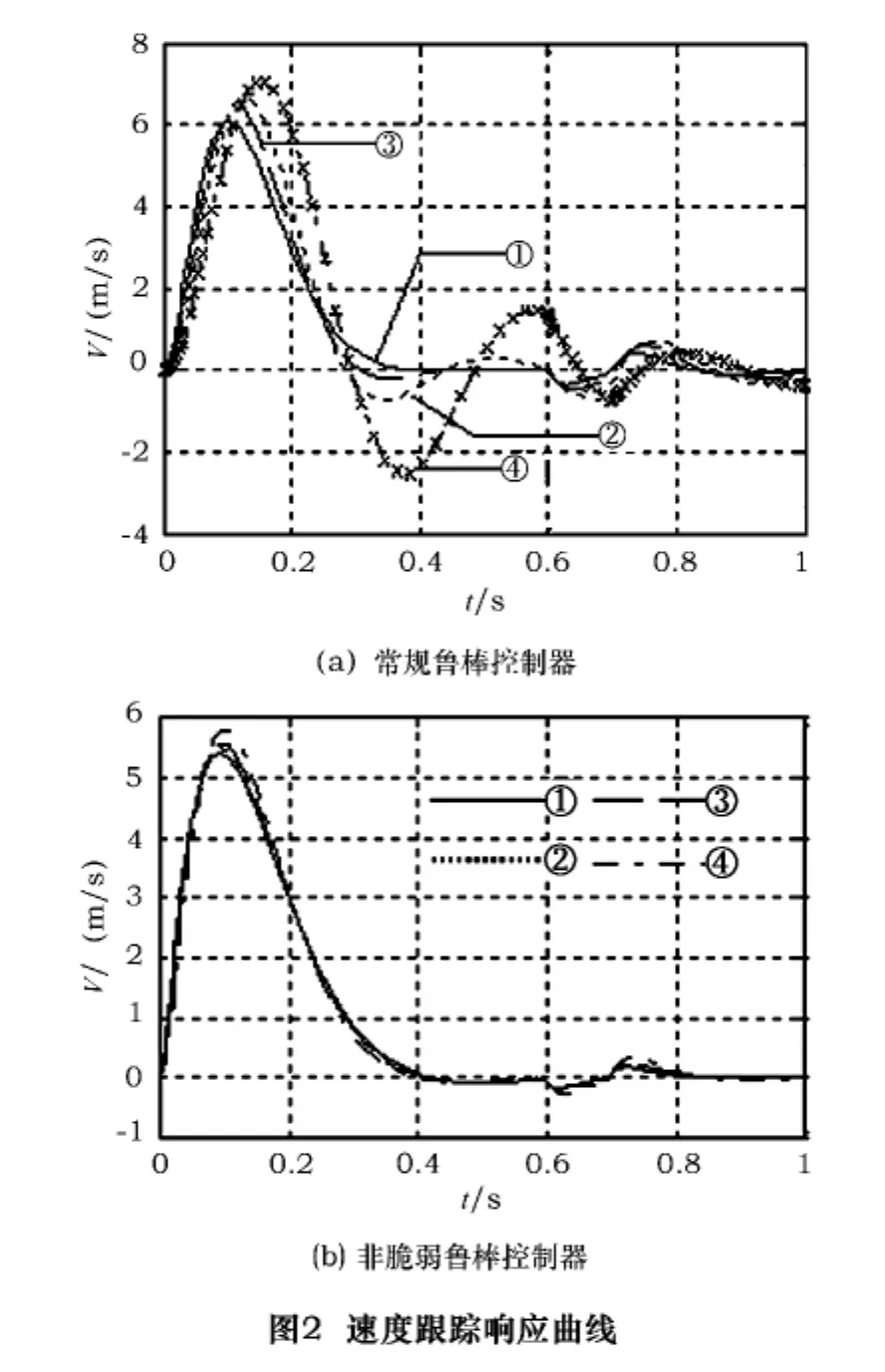
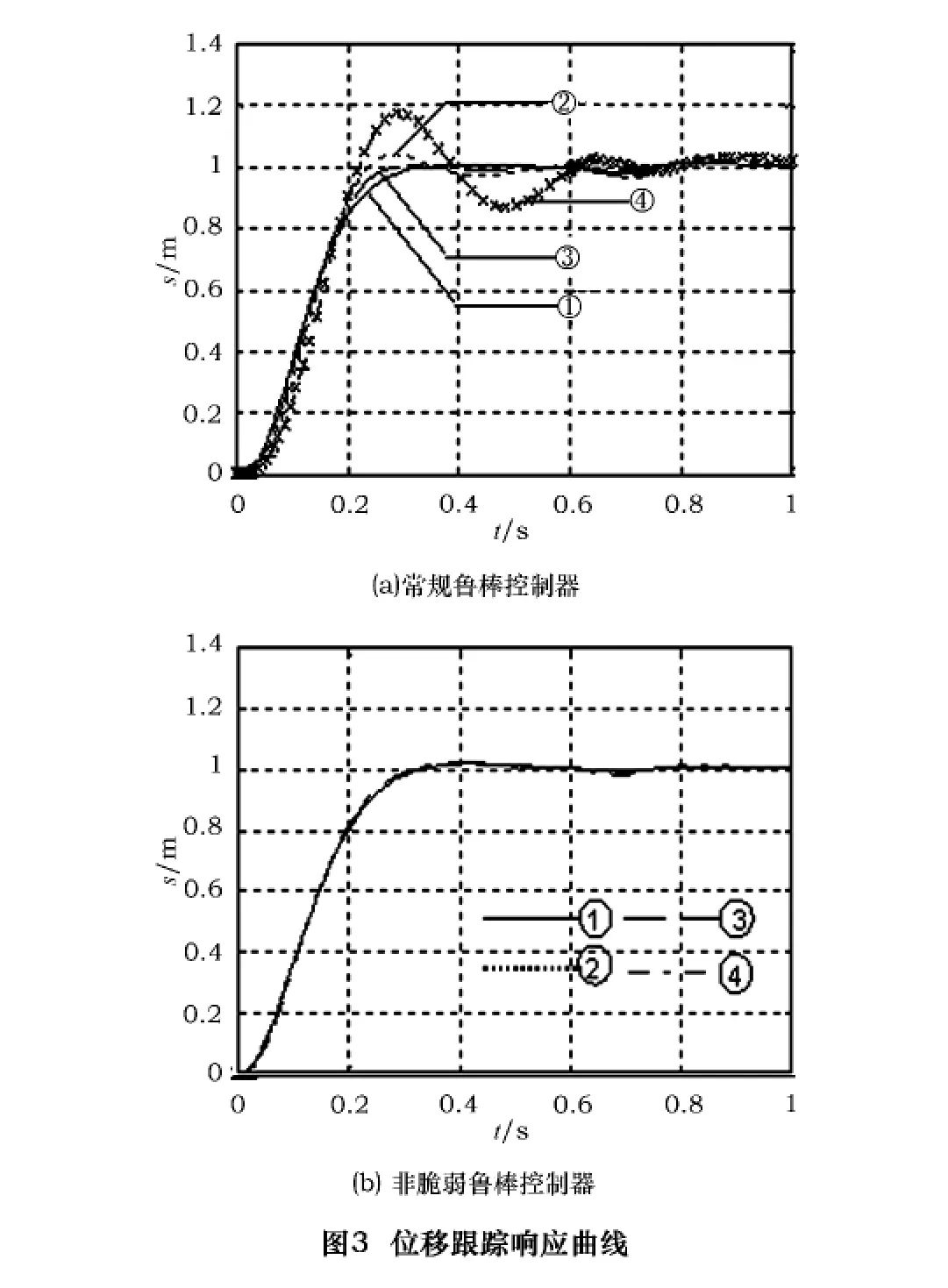
在外部扰动作用下将常规鲁棒控制器与本文设计的非脆弱状态反馈控制器做仿真比较，如图1～3。图1～3中曲线1为无摄动情况。可以看出本文的非脆弱鲁棒控制器具有良好的干扰抑制作用。由图知，在增益摄动影响下，常规鲁棒控制器对于增益摄动比较敏感，超调量增大，调节时间变长，性能下降，显示出脆弱性。非脆弱控制器的状态曲线是否存在增益摄动，无明显变化，曲线基本吻合。说明本文设计的控制器既是鲁棒的，又是非脆弱的。

4 结语

在磁悬浮永磁直线电动机状态空间模型基础上，研究了非脆弱鲁棒控制器可行的充分条件。根据H∞性能指标与线性矩阵不等式的等价性，将设计问题转化为对LMI的求解，得到磁悬浮永磁直线电动机系统的非脆弱鲁棒H∞控制器。通过与常规鲁棒控制器仿真比较，表明该方法的有效性。

［1］曹杨，祝长生.磁悬浮列车用永磁直线同步电动机特性的有限元分析［J］.电气应用，2006，25(12):25 －28.

［2］夏加宽，王成元，李皥东，等.高精度数控机床用直线电动机端部效应分析及神经网络补偿技术研究［J］.中国电动机工程学报，2003，23(8):100－104.

［3］徐月同，傅建中，陈子辰.永磁直线同步电动机进给系统H∞控制策略的研究［J］.浙江大学学报:工学版，2005，39(6):789 －794.

［4］石颉，王成山.基于线性矩阵不等式理论的广域电力系统状态反馈控制器设计［J］.电网技术，2008，32(6):36 －41.

［5］安海云，贾宏杰，余晓丹.基于LMI理论的时滞电力系统无记忆状态反馈控制器设计［J］.电力系统自动化，2010，34(19):6 －10.

［6］姚成法，侯明善，杨常伟，等.LMI方法非脆弱鲁棒H∞控制器设计［J］.电光与控制，2007，14(6):85 －88.

［7］Keel L H，Bhattacharyya S P.Robust，fragile ，or optimal［J］.IEEE Trans .on Automatic Control，1997，42(8):1098 －1105.

［8］唐任远.现代永磁电动机理论与设计［M］.北京:机械工业出版社，1997.

［9］杨俊友，刘江华，邱桂林，等.基于预测电压调制与 T－S模糊PMLSM 推力控制［J］.沈阳工业大学学报，2012，34(4):361 －365.

［10］申铁龙.H∞控制理论及应用［M］.北京:清华大学出版社，1996.