关于一个初等数论问题的解答与推广

刘春辉

（赤峰学院 教务处,内蒙古 赤峰 024000）

1 问题的引入

《初等数论》是数学及其相关专业的一门重要的基础性课程，数论问题的解答在培养学生的逻辑思维能力和提高学生的数学素养方面都发挥着至关重要的作用.因此，在教学实践的过程中，教师都十分重视对学生解题能力的训练.由此，也大大提升了广大教师和学生对许多有趣的数论问题进行解答和深入思考的浓厚兴趣.由王进明[1]主编的《初等数论》一书的习题1.3中有如下一道很有趣的习题：

某位同学没有注意写在两个七位数之间的乘号，将其误认为是一个14位数，有趣的是此14位数正好是原来两个七位数乘积的三倍，试求出这三个数.

本文将给出该问题的一个完整的解答，并结合在教学实践中对该问题的进一步思考，对其作一般性推广，在获得了一般性结论的同时，还得到了一个十分有趣的计算结果.

2 问题的解答

上述问题完整的解答过程如下：

设乘积中的两个七位数分别为A和B，14位数为C，则由题意可得

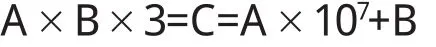
从而可得

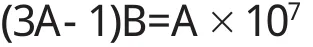
又因为

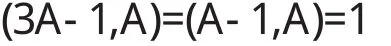
所以由[1]中定理1.3.13可得

又因为A和B都是七位数，所以可设

故由3整除一个正整数的特征得

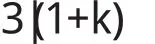
从而k的所有可能的取值为

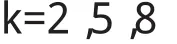
（I）当 k=2时，有 6A=107+2，解得 A=1666667，此时B=2A=3333334，于是C=16666673333334；

（II）当k=5时，有15A=107+5，因为最小的七位数为106，而15×106>107+5，所以A无解.

（III）当 k=8时，有 24A=107+8，因为最小的七位数为106，而24×106>107+8，所以A亦无解.

综上所述，所求的两个七位数分别为

3 问题的推广

以上是关于一个14位数恰好等于两个七位数乘积的三倍问题的求解过程.事实上，这个问题可以推广为关于两个n位数与一个2n位数的关系的一般性问题，具体讨论如下：

是否存在两个n位整数

以及一个2n位整数

使得3AB=C.

解 假设满足条件的整数A，B和C存在.则由题意可得

又因为A和B均为n位数，所以可设

故由3整除一个正整数的特征得

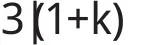
从而k的所有可能的取值为

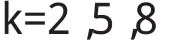
（I）当 k=5时，有6A=10n+2

若 n=1，则

A=2，B=2A=4，C=10A+B=24

若 n≥2，则

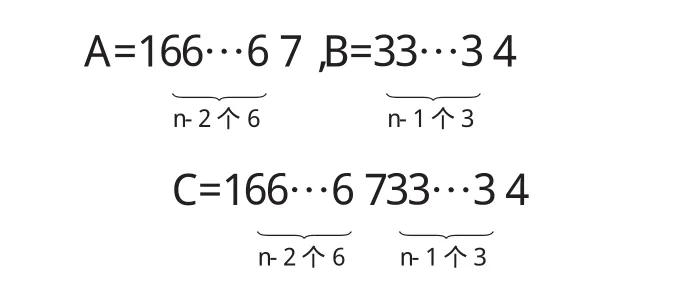
（II）当 k=5时，有 15A=10n+5

若 n=1，则

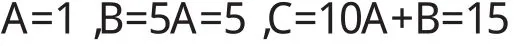
若n≥2，因为最小的n位整数为10n-1，而15×10n-1>10n-1+5，所以此时A无解.

（III）当k=8时，有24A=10n+8.因为最小的n位整数为10n-1(n≥1)，而24×10n-1>10n+8，所以此时A亦无解.

综上所述，可得结论如下：

至此，我们对推广后的问题给出了一个完满的回答.此外，如果对上述解答过程再做进一步的深入思考，不难发现如下的一系列有趣的计算规律：

〔1〕王进明.初等数论[M].北京:人民教育出版社,2002.