基于Crank-Nicolson格式的输运方程的数值求解方法

魏丙涛

（文山学院 数理系，云南 文山 663000）

输运方程是数学物理方程中比较重要的方程之一，能够描述一些输运的物理过程，比如：制作半导体器件就常用到扩散法，把含有所需杂质的物质涂敷在硅片表面，把硅片放在扩散炉里，杂质就向硅片里面扩散，扩散运动的方向基本上是垂直于硅片表面而指向硅片深处[1]，这种只沿某一方向进行的扩散就可以用一个一维的输运方程来描述这一物理过程.输运方程的解法很多，一般的输运方程是可以用解析的解法求解的，对于复杂的方程、边界条件及初始条件，解析解就变的比较困难了，于是需要寻求数值解法.对于偏微分方程，数值解法一般采用有限差分法，在此介绍一种基于Crank-Nicolson格式的差分方法的数值求解.

本文第一部分将对Crank-Nicolson格式做个简单的介绍，第二部分将给出数值结果，第三部分则是本文的结论.

1 Crank-Nicolson格式简介

考虑如下的定解问题：

上述方程是一个输运方程，该方程的最基本差分格式为向前差分和向后差分格式，向前差分格式可以写为[2]：

可以将这个差分格式改写为：

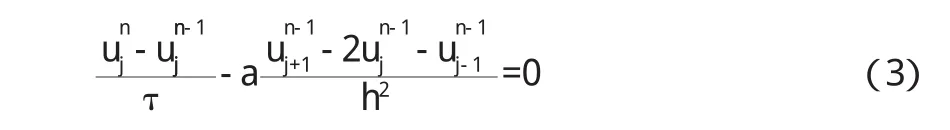
向后差分的的格式可以写为[3]：

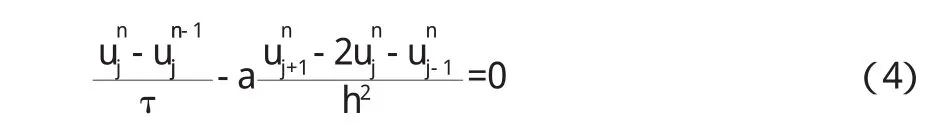
在（4）式的等式左右两边同乘θ，在（3）式的两边同乘(1-θ)，并将两式相加得到[4]：

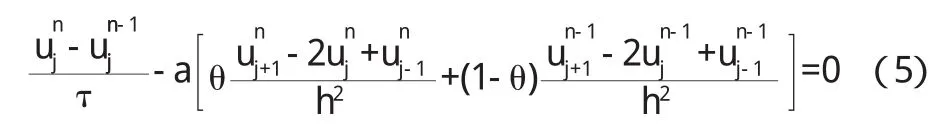
上式为加权隐格式的差分格式，在上面的式子中，λ表示时间步长，h表示空间步长，θ是一个大于0小于1的数，当θ=0时上式成为向前差分格式，当θ=1时上式变成向后差分格式.

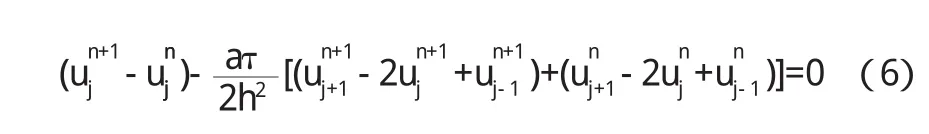
这个格式一般称作Crank-Nicolson格式，这个差分格式是无条件稳定的，这会给数值解法带来很多方便.

2 数值结果

定解问题（1）能够给出解析解，在此取a=1，其解析解为：

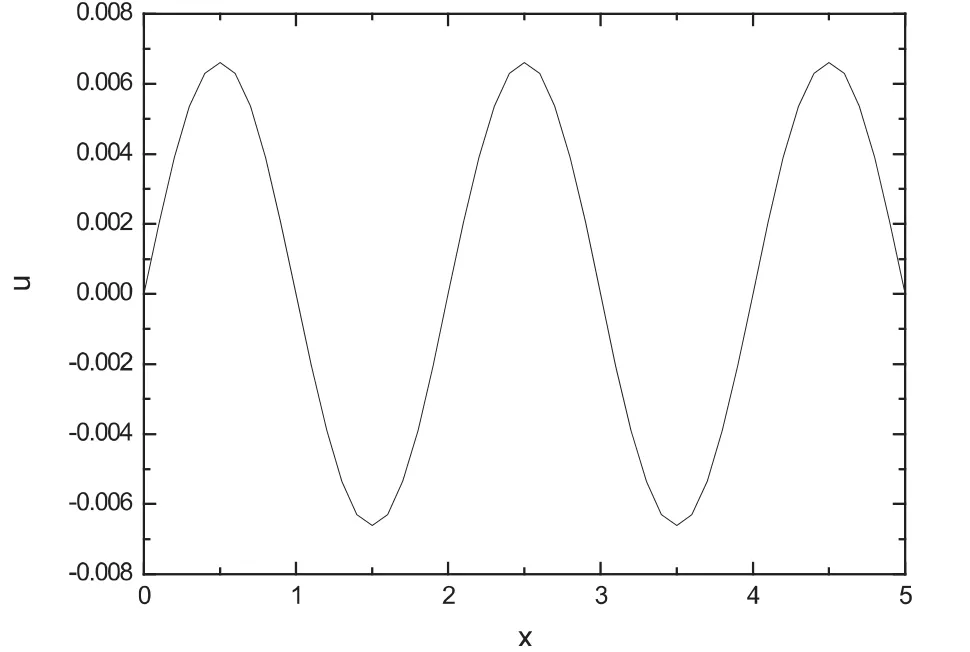
图1 t=0.5时Crank-Nicolson格式下的数值解

图2 t=0.5时定解问题的解析解的函数图像

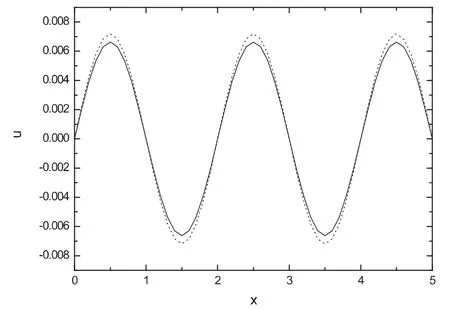
图3 t=0.5时Crank-Nicolson格式的数值解与解析解之间的差别，虚线是解析解的函数图像，实线为Crank-Nicolson格式下的数值解

图1给出了t=0.5定解问题的数值解，图2给出了t=0.5时的解析解的函数图像，图3给出了t=0.5两种解法之间的比较，图4给出了函数值u随时间t及坐标x变化的函数关系图.从图中可以出，数值解与解析解之间的误差很小，数值解也是稳定的，并且Crank-Nicolson格式是绝对稳定的，这对于数值解是很有用的.

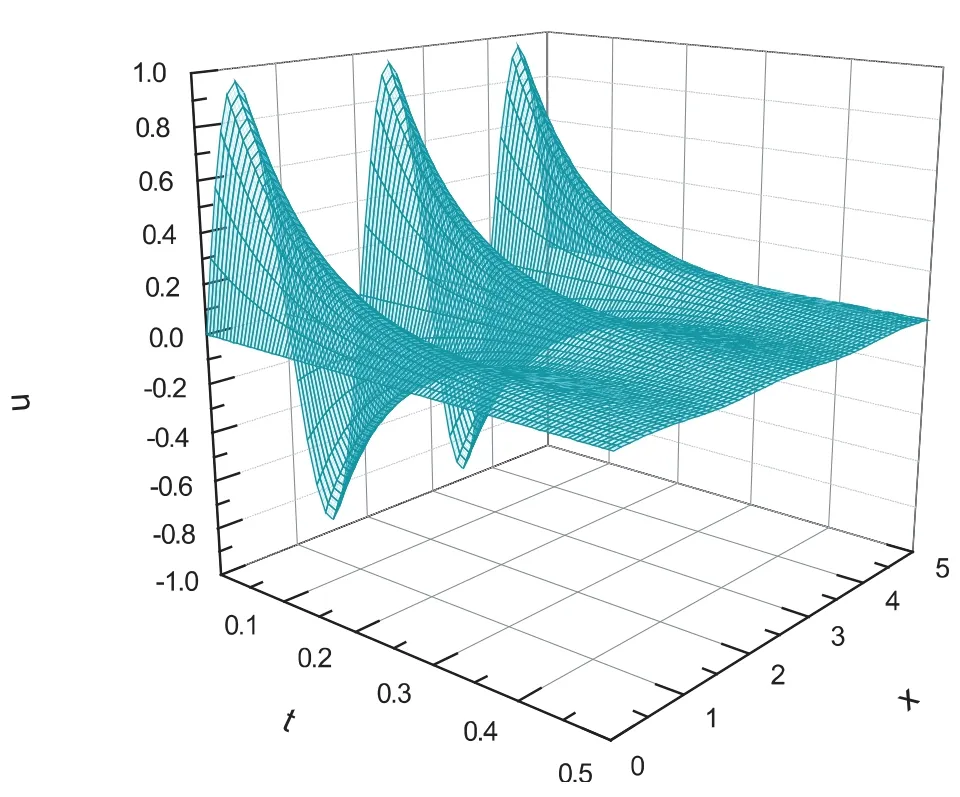
图4 函数值u随时间t及坐标x变化的函数关系图

3 结论与讨论

通过上面的计算可知，Crank-Nicolson格式是一个觉得稳定的格式，并且这种算法的精度比较高，在实际的数值求解过程中非常有用.这个差分格式适用于输运方程的数值求解中，虽然有很多输运方程很容易得到解析解，但数值解法在很多时候很多方面是具有优越性和适用价值的.

〔1〕梁昆淼.数学物理方法[M].北京：高等教育出版社，1998.

〔2〕Ames W F.Numerical Metheds for Partial Differential Equations.2nd ed.New York:Academ ic Press,1977.

〔3〕徐长发,李红.偏微分方程数值解法[M].武汉:华中科技大学出版社,2000.

〔4〕陆金甫,关治.偏微分方程数值解法[M].北京:清华大学出版社,2004.