概率在日常生活和工作中的应用

郑艳霞

（中国青年政治学院 经济系，北京 100089）

和经典数学分支相比，概率是一门“年轻”的学科，这门学科到目前还有许多不完善的地方，但就它已得到的成果，已经给人类活动的诸多领域带来了一场革命.这场革命也改变了人们的思维方法，如果我们运用概率的知识来重新分析和认识自己生活和工作中的问题，不但能对以往的经验找到数学的理论依据，而且会得到与以往思维模式不同的答案，而理性的思维方式会让我们变得更聪明，更有智慧.

1 只要功夫深，铁杵磨成针——概率告诉我们持之以恒的力量

某人英语基础薄弱，目前只有高中生的英语水平，工作需要他5年之后必须去英国，并且需要运用英语开展工作.可是他现在的工作十分繁忙，无法抽出大量的时间来集中学习英语，于是他制定了一份特殊的学习计划——每天抽出30分钟时间来学习英语.我们帮他分析一下，他5年后能够运用英语工作的可能性有多大？

按照北京语言大学出国留学人员英语培训的科目资料显示：英语听说读写全能业余班培训初级班共需要120小时，中级班120小时，高级班120小时.按照该人需要达到中级班培训合格的水平计算，每天30分钟的时间学习英语知识对于实现目标的可能性非常小，仅仅为p=0.002083左右.设Ai={第i天学习成功}且Ai相互独立,i=1,…,n.再设A={五年后能够运用英语工作}，5年有 1825天，当 n=1825时，P(A)

若该人想要达到高级班培训合格的水平，p=0.0014，P(A)=1-(1-p)n=92.24%.

由计算结果可以看出，只要此人每天坚持花30分钟时间努力学习英语，这个人5年后能够运用英语工作的可能性为97.84%，这几乎说只要他每天坚持努力，5年后能运用英语工作是自然而然的事情；就是自如运用英语进行工作也有九成以上的把握.因此人要是想增加一件事情成功的把握，一个方面是增加事情本身成功的胜算，也就是增大p值.如果本身事情成功的胜算不大甚至于很小，只要坚持不懈的努力，也就是增大n的取值依然可以增大成功的可能性，而且长时间坚持不懈的努力，会把一件希望渺茫的事情变成必然.这也是对“只要功夫深，铁杵磨成针”的最好诠释.

2 三个臭皮匠，顶一个诸葛亮——概率告诉我们团队合作的力量

常言道：“三个臭皮匠，顶一个诸葛亮”.这是对人多办法多，集体力量大的一种赞誉，这也可以由概率的计算得到证实.假设三个臭皮匠能独立解决某问题的概率分别为0.45，0.55，0.60,问三人合力能解决该问题的可能性是多少？

将三人编号为1,2,3,记Ai={第i个人能解决该问题}，i=1,2,3.解决上述问题关键是求P(A1∪A2∪A3).已知P(A1)=0.45，P(A2)=0.55，P(A3)=0.60，且 A1，A2，A3相互独立，因此

看！三个并不聪明的臭皮匠，能以90%以上的概率解决问题，聪明的诸葛亮也不过如此嘛.可见团队合作是非常重要的.由此可见，在一个团队中，只要能够集思广益，把大家的优势都发挥出来，力量比拥有几个“智者”大得多.

3 未雨绸缪——概率指导我们科学看待体检，防病治病

一项血液化验有95%的把握将患者某种癌症鉴别出来.但是，这项化验用于检测健康人也会有5%的人呈现阳性（即把健康人误诊为患癌症的概率为5%）.如果该种癌症的患者实际占人口的0.5%，而某人化验结果是阳性，问此人患该种癌症的概率是多少？如果某人化验结果是阳性，该怎么办？

我们首先分析如果某人的体检结果呈阳性，他患有癌症的风险有多大.假设A={化验结果为阳性}，B={此人患该种癌症}，B={此人健康}，由贝叶斯公式有

计算结果表明，若该人进行试验且结果为阳性，则此人确实患癌症的概率为P(B1|A)=0.087.也就是说即使检查的结果呈阳性也不必过早下结论该人患有癌症，这种可能性只有8.7%，即平均每1000人中大约只有87人确患有该种癌症.但是这种试验对于诊断一个人是否患有癌症是有很大意义的.如果不做试验抽查一人，他是患者的概率P(B1)=0.005；若作试验且是阳性结果，则他是患者的概率为P(B1|A)=0.087，患癌症的风险提高十七倍多，起到了很好的警示作用.

如果某人体检结果显示为阳性，在保持乐观精神的同时提高对该种癌症监测力度是必要的.下面用贝叶斯公式计算监测的用处.设 Ai={第 i次化验结果为阳性，i=1，2，3}，B={此人患该种癌症}，B={此人健康}，由贝叶斯公式有

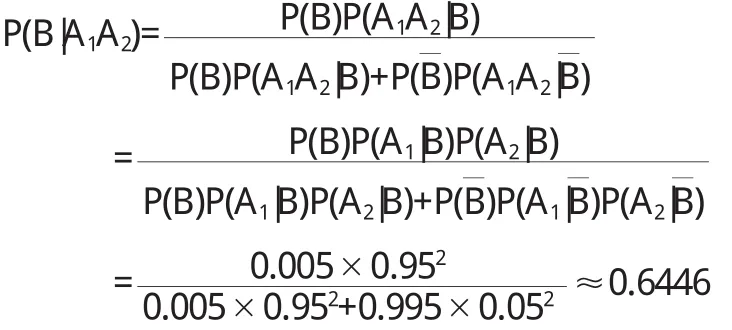
这说明体检结果呈现阳性，隔一段时间再去监测，如果监测结果仍然是呈阳性的，此时患癌症的风险已经过半，必须提高警惕了，应该在积极就医的情况下保持良好心态并继续进行监测.

再过一段时间再去监测，假如结果仍然呈阳性，几乎可以肯定该人是患了癌症，因为

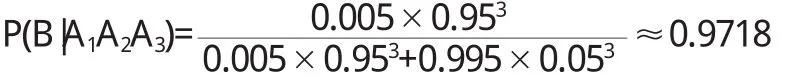
运用概率的知识让我们能够更加客观的看待医学检查，既不是悲观失望，被检查结果吓倒，同时又采取科学的态度进一步监测，用正确的方法指导就医.

4 抓住真凶——概率给我们一双“慧眼”，认清嫌疑犯

1981年3月30日，美国大学退学学生Hinckley企图对里根总统行刺，他打伤了里根总统、里根总统的新闻秘书以及两个保安人员.1982年，Hinckley因为犯有谋杀总统的罪名而被起诉，审判他时，Hinckley以精神病为理由为自己作无罪的辩护.Hinckley的辩护律师拿出Hinckley的CAT扫描作为证据争辩说，因为Hinckley的扫描展示了脑萎缩，因而他患有精神病的可能性更大些.作证的医师是Daniel R.Weinberger告诉法院当被诊断为精神分裂症的人进行CAT扫描(计算机辅助层析扫描)时，扫描结果有30%的案例显示为脑萎缩，而只有2%的正常人扫描显示脑萎缩.最后在辩护人的有力辩护下，Hinckley被判无罪.那么辩护律师提供的关于脑萎缩证据足以说明Hinckley患有精神病吗？

从表面上看，Hinckley辩护律师的辩护似乎很有说服力，能够证实Hinckley是精神病患者.下面我们用概率的方法验证一下辩护律师的结论.通过收集医学资料可以知道，在美国精神分裂症的发病率大约为1.5%.设事件A={脑萎缩}，B={患有精神病}，由贝叶斯公式有

计算结果表明，在Hinckley的CAT扫描结果是脑萎缩的前提下，他患有精神病的可能性只有18.6%，显然辩护律师仅仅用CAT扫描结果是脑萎缩来证明Hinckley患有精神病，证据的说服力很弱，如果想证明Hinckley确实患有精神病，还应该提供其他更有力的证据才行.

由此可见，我们通常得到的一些结论在表面上看似乎很有道理，但是运用概率知识进行分析和计算，就会发现其实有些结果与我们的直觉是不一样的.甚至可以得出截然相反的答案来.

5 “3σ原则”助力高考作文阅卷——概率让感性的工作增加客观公正的筹码

“3σ原则”指的是，若随机变量X服从参数为μ和σ2的正态分布，则P(|X-μ|<3σ)=0.9974.也就是说，如果随机变量是服从参数为μ和σ2的正态分布，则随机变量的1000个取值平均有997个以上分布在以μ为中心以3σ为半径的区间内.也就是说，随机变量取值非常大或者非常小都是很少的.

“3σ原则”在工业上普遍使用，现在其他行业也开始使用该原则，比如现在高考语文的作文评分中就使用了该原则.大家都知道，语文作文的评分很难，有的老师觉得这篇作文结构紧凑，文字优美就给出高分，甚至给出满分，而同样一篇作文假如换另外一位老师判卷，可能就是另外的分数，中间的分数差异可能很大，这就给考生的成绩带来不小的变化，而高考成绩是决定人命运的大事，因此如何建立相对公平的给分体系，是教育专家们考虑的一个重要问题.由概率知识可知高考语文作文成绩服从正态分布，于是引入概率统计中的“3σ原则”，来干预高考的语文作文阅卷工作.大致的作法是：请一批包括大学教授在内的最有声望的作文老师团队来判分，发现他们的分数判的比较准确、稳定，分数相差不多，因此用他们的分数作为统计数据来确定当年的作文分数的期望μ和方差σ2，给出当年高考作文的平均值及分数的波动的上下限来.在高考语文作文阅卷过程中，不断检查每位阅卷教师所给出的作文分数，如果阅卷老师给出的分数在允许的范围之内就通过，认为阅卷老师给出的是合理的分数，否则马上警告这一小组要小心，如果再出现一个奇异分数，就将该组试卷全部重判，甚至请专家组介入判卷过程，只有经过多人重复确定的奇异分数才会有效，以此保证给出的作文分数更加合理.“3σ原则”在高考语文作文判卷中的使用，对于极高或者极低分数的作文成绩起到警戒作用，对于高考语文作文判卷这项主观性很强的工作增加理性的衡量，对于判分的公平性起到了很好的作用.

6 免费抽奖问题——概率让我们认清商家的促销活动

某电子产品公司推出了一个非常有吸引力的抽奖活动：“本公司为了答谢广大用户长期以来的支持与厚爱，特别推出免费抽奖活动.抽奖方式为：箱子里有20张卡片，10张上标有数字10，另外的10个上标有数字5.从箱子里摸出10张卡片，把各卡片上的数字相加，按数字之和设置奖项如下：

?

“抽奖结果共有 11个，即 50、55、60、65、70、75、80、85、90、95、100分.其中有10个分数可免费得到奖品，中奖率超过90%”.

这样的宣传从直觉上非常有诱惑力，但是如果我们仔细观察，就会发现实际上情况与我们想象的有很大的差异，顾客参加抽奖活动即便中奖也几乎都是非常小的奖项，能够中六等奖以上的奖项非常稀少，大部分中奖的顾客都是DVD盘盒，或者可以购买5折U盘.下面我们运用概率知识，详细解读商家的抽奖活动.

分析可知，这是一个超几何分布，设Ai={抽出10张卡片中含有数字 10的个数}，i=0，1，2，……，10，则 P(Ai)=.经过计算可以得到中各种奖的概率如下

?

再进一步调查各种奖项的成本，得到下面的信息：

?

计算商家的平均收益为：

由此可见，这场看似热闹的抽奖活动，其实是商家促销的一种手段.实际上商家在扩大自己的知名度、免费进行了广告宣传的同时还是稳赚不赔的.而商家宣传的中奖率超过90%的概率只是迷惑顾客的方法.这11种情况出现的概率大小差别非常大，而通常我们会认为各种情况出现的可能性是均等的，商家借此概念的混淆来迷惑顾客.

由于随机现象在现实世界中大量存在,概率越来越显示出它巨大的威力.其实，我们日常生活中到处都有概率的影子，小到每天的天气预报，大到航空母舰的制造，都离不开概率统计，在经济活动和实际的生活中，有许多问题尤其是决策问题可以直接或间接地利用概率结论来解决，或者可以应用概率给出有价值的参考意见.

〔1〕郑艳霞，邓艳娟.高等数学基础教程[M].北京：清华大学出版社，2010.

〔2〕中央电视台《百家讲坛》栏目组.相识数学[M].北京：中国人民大学出版社，2006.

〔3〕林志兴.概率与直觉[J].数理统计与管理,2006(2)：240-243.