高采样率下GPS卫星轨道坐标插值方法比较*
王青平 陈 光 陈超贤 赵文波
(福建省地震局,福州 350003)
高采样率下GPS卫星轨道坐标插值方法比较*
王青平 陈 光 陈超贤 赵文波
(福建省地震局,福州 350003)
比较拉格朗日、牛顿与内维尔3种插值算法的运算量、精度和运行时间。结果表明:在精度要求范围内各算法均是可取的,但拉格朗日插值在插值节点两端易产生龙格现象;在50 Hz采样率插值实验中,多项式系数求解法的运行时间仅为拉格朗日插值的1/45,为牛顿和内维尔插值的1/15。
GPS精密星历;拉格朗日插值;牛顿插值;内维尔插值;多项式系数求解法
1 引言
GPS定位是在GPS卫星的空间坐标已知的情况下,通过测量卫星至天线的距离来计算天线的空间坐标。因此快速而准确地获取卫星的空间坐标是GPS定位首要解决的关键问题。
获取GPS卫星的轨道坐标通常有两种途径[1]:一种是根据广播星历计算出星历参数,进而求出卫星的空间坐标,另一种是根据精密星历计算卫星轨道坐标。广播星历每两小时更新一次,实时发送给用户,精度为2 m;精密星历由IGS等国际组织发布,包括最终精密星历(igs)、快速精密星历(igr)以及预报精密星历(igu)[2],目前最终精密星历有12~18天的延迟,GPS最终精密星历标称精度为2.5 cm、GLONASS标称精度为5 cm,被广泛应用于事后高精度定位。特别是近些年兴起的非差精密单点定位技术(PPP,Precise Point Positioning),它利用 IGS提供的精密星历获得单台测站厘米级的定位精度[3]。精密星历的插值精度以及计算效率将直接影响到PPP等事后高精度数据处理的精度和效率。
精密星历文件每15分钟更新一次卫星的坐标,而GPS接收机的采样率一般为30秒、1秒甚至更高,需要用插值的方法得到所需历元的卫星位置。快速而准确地对精密星历进行插值成为GPS数据处理中的一项重要工作,特别是高频采样[4]。
在实际应用中,选用何种插值算法、选用几次多项式可满足实际的精度要求,时常成为困扰众多用户的问题。为此,本文将给出各插值算法的理论乘/除法运算量,以精密星历给出的卫星轨道坐标为原始数据,比较三种不同采样率下各种插值程序算法的实际运行时间,并对其插值结果进行分析。
2 插值算法
2.1 常用的插值算法
常用的插值算法有拉格朗日多项式插值[1,5-11]、牛顿多项式插值[6,7,10]、内维尔逐次线性插值[1,5,9,10]以及三角函数插值[8]等。
拉格朗日插值模型简单,形式对称,是经典的插值方法,但是当精度不满足要求而需要增加插值节点时,原来的插值多项式不能使用,需重新构造新的插值多项式;而牛顿插值和内维尔逐次线性插值在增加新的插值节点时,可以重新利用前面的计算结果,常用于给定精度的变阶次多项式插值;三角函数插值基于GPS卫星轨道的准周期性,选用三角函数作为基函数,物理涵义清晰,但过程中涉及到大量三角函数运算,运算量较大。
2.2 插值多项式的阶次
选用几次多项式对GPS卫星的空间坐标进行插值,使得插值的精度最高,许多学者对此做了研究:张守建[8]认为10阶拉格朗日多项式内插精度最高,11阶的三角函数多项式插值内插精度最好;邱蕾[9]认为当插值点位于节点中央时,9阶以上拉格朗日和内维尔插值可获得与精密星历相当的精度,同时多项式的次数最好为奇数,待插值的时刻位于节点的中间,插值的误差也最小;马俊[10]认为拉格朗日、牛顿以及内维尔插值在16阶精度最高;何玉晶[11]认为9阶拉格朗日插值的精度最高;王晓明[1]则提出一种高阶插值与低阶插值相结合的插值算法来提高插值精度。虽说众学者的看法不尽相同,但均认为在进行多项式插值时,适当提高多项式的次数,可以提高插值的精度,但在插值节点两端附近高次多项式插值,容易产生龙格(Runge)现象[6,7],特别是拉格朗日多项式插值[10],因而会影响整个插值的精度,故盲目地提高插值多项式的次数是不可取的。为简单起见,本文只考察13次多项式的各种插值算法。
2.3 多项式系数求解法
对于n次多项式:
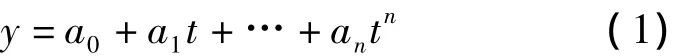
把t0,t1,…,tn卫星的空间坐标y0,y1,…,yn代入后,可得n+1个关于多项式系数a0,a1,…,an线性方程组,可通过高斯消去法可求解得多项式系数a0,a1,…,an,再利用秦九韶算法[6]可求出插值区间内任意时刻卫星的空间坐标。
多项式系数求解法[6]需解线性方程组,计算量稍大,早期的采样率较低,故没有得到广泛的应用。
3 插值算法的比较
3.1 理论运算量的比较
表1为不同几种插值算法对m个插值点进行插值的理论乘/除法运算量[5-7]。拉格朗日插值、牛顿插值以及内维尔插值的时间复杂度均为O(mn2)。多项式系数求解法先用O(n3)的运算量计算出多项式的系数,后续使用秦九韶算法对m个插值点求值仅需O(mn)的运算量,总运算量为O(n3+mn)。
牛顿插值的乘/除法运算量仅为拉格朗日插值的1/4,为内维尔插值的1/3,是一种比较理想的插值方法。但是当GPS接收机采样率较高时,所需要的插值点m也越多,特别是当m≫n时,多项式系数求解法占有绝对的优势。

表1 各插值方法理论乘/除法运算量的比较Tab.1 Comparison of computation of different interpolation methods
3.2 理论曲线计算结果的比较
考虑到GPS卫星运行的周期性,选用下列函数作为理论曲线进行比较:
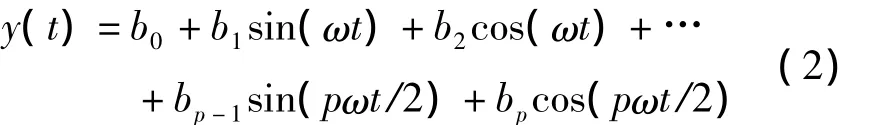
式中b0,b1,…,bp为系数,ω 为圆频率。张守建[8]认为11阶的三角函数多项式与卫星空间坐标拟合较好。随机产生一组b0,b1,…,b11进而产生14个插值节点(图1中的红色标记),进行各种多项式插值(n=13),并将插值结果与式(2)的理论值进行比较,误差分布如图2所示。不难看出:
1)各算法的绝对误差量级都是很小的。在精度要求范围内,各种算法均是可行的;
2)各算法在中央区域的绝对误差都很小。在实际插值过程中,待插值的时刻最好位于插值节点中央区域附近,使得插值的误差最小;
3)拉格朗日多项式插值在插值区间两端附近绝对误差较大,出现剧烈的龙格震荡现象。
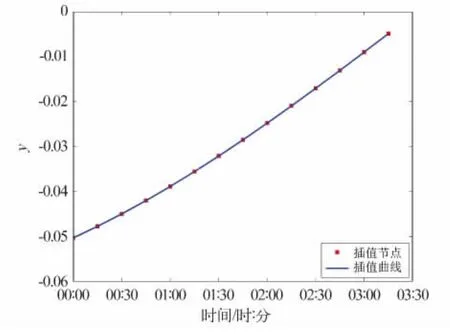
图1 插值节点和插值曲线Fig.1 Interpolation nodes and interpolation curve
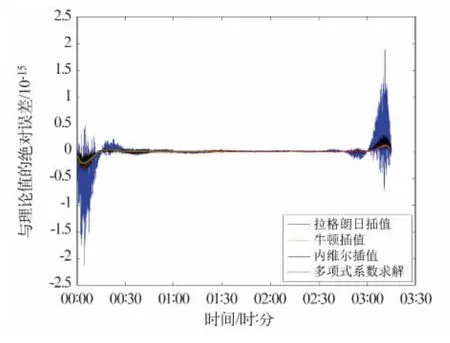
图2 不同插值算法与理论值的绝对误差Fig.2 Absolute error of different interpolation algorithms with the theoretical value
3.3 实际卫星空间坐标计算结果的比较
从 IGS 网站(ftp://garner.ucsd.edu/pub/products/1721/igs17212.sp3.Z)下载 igs17212.sp3 精密星历文件:历元始于 2013-01-01T00:00:00,止于2013-01-01T23:45:00。选用前14个历元序号为1的卫星的横坐标作为插值节点,对中央区域(1时30分至1时45分,图3中蓝色区域)进行1 Hz的采样插值。
因无法悉知非插值节点处卫星的真实坐标,只能通过比较四种插值算法间的离散程度。图4给出四种插值算法的计算结果间的最大误差分布,很明显四种插值算法在该区间中差异都很小,并且分布均匀。表明待插值的时刻位于插值节点的中央时,无论使用何种算法,计算结果均可取。
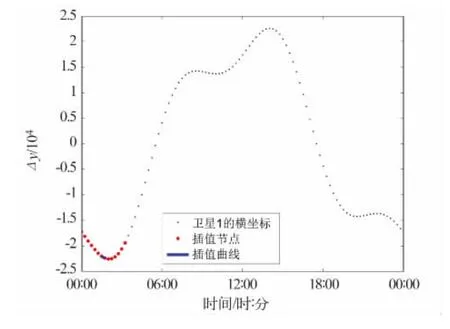
图3 卫星的精密星历以及插值节点分布Fig.3 IGS precise ephemeris and interpolation nodes distribution
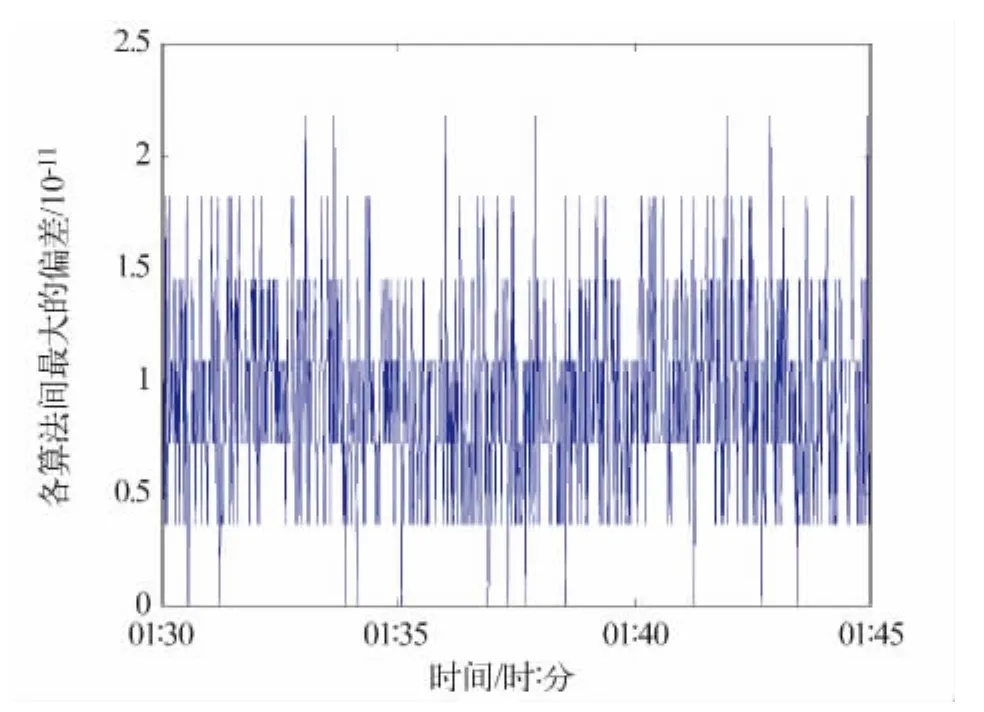
图4 各算法间的最大偏差分布Fig.4 Maximum error distribution among the interpolation algorithms
3.4 计算时间的比较
使用各插值算法分别对30 s、1 Hz以及50 Hz采样率的插值点进行插值,表2给出四种算法的运行时间(代码通过MinGW GCC编译,运行环境为I5的CPU、4G内存、Win7操作系统),不难看出:
1)拉格朗日多项式插值算法的运行效率很低;
2)牛顿插值与内维尔插值的运行时间相当,运行时间约为拉格朗日插值的1/3;
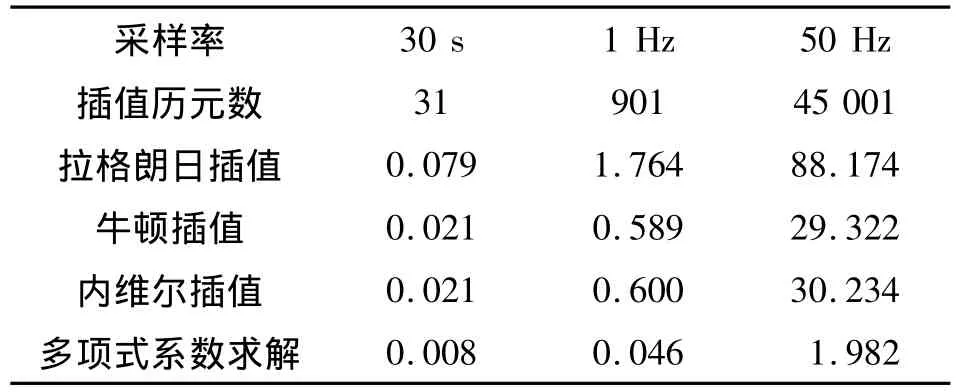
表2 各插值方法的运行时间(ms)Tab.2 Running time of different interpolation algorithms(unit:ms)
3)多项式系数求解法的效率相当高,与其他三种算法相比均有一个量级的提升,且采样率越高性能提升得明显。特别是50 Hz采样率运行时间仅为拉格朗日插值的1/45,为牛顿插值以及内维尔插值的1/15;
4 结论
1)拉格朗日插值、牛顿插值和内维尔插值算法的时间复杂度均为O(mn2),而多项式系数求解法的时间复杂度为O(n3+mn)。
2)当待插值的历元位于插值节点中央时,无论采用哪种算法进行插值,都能取得满意的结果。当待插值的历元插值节点区间两端附近时,牛顿插值和多项式系数求解法最为稳定,而拉格朗日插值极易产生龙格现象;
3)多项式系数求解法的运行效率最高。50 Hz采样率下,其效率约为牛顿插值和内维尔插值的15倍;约为拉格朗日插值的45倍。
由于早期接收机的采样率较低,多项式系数求解法并没有得到广泛的使用。随着科技的发展,主流接收机均朝着高采样率方向发展,相信不久的将来多项式系数求解法将得到广泛的应用。
1 王晓明,成英燕,刘立.基于阶次组合的GPS精密星历插值研究[J].大地测量与地球动力学,2011,(4):103-106.(Wang Xiaoming,Cheng Yingyan and Liu Li.Research on GPS precise ephemeris interpolation based on high/low order integrated[J].Journal of Geodesy and Geodynamics,2011,(4):103 -106)
2 刘伟平,等.GPS轨道实时预报对比研究[J].大地测量与地球动力学,2012,(1):94 -96.(Liu Weiping,et al.Comparison and study on real-time prediction of GPS orbit[J].Journal of Geodesy and Geodynamics,2012,(1):94 -96)
3 郝明,王庆良,崔笃信.GPS精密单点定位快速收敛方法研究[J].大地测量与地球动力学,2009,(2):88-91.(Hao Ming,Wang Qingliang and Cui Duxin.Study on fast convergence method in precise point positioning[J].Journal of Geodesy and Geodynamics,2009,(2):88 -91)
4 吴继忠,吴文坛.利用高频GPS进行地震动态变形分析及地震定位[J].大地测量与地球动力学,2012,(2):20-23.(Wu Jizhong and Wu Wentan.Kinematic analysis of coseismic deformation and seismic location using high-rate GPS[J].Journal of Geodesy and Geodynamics,2012,(2):20-23)
5 William H Press,et al.Numerical recipes:The art of scientific computing(3rd edition)[M]:New York:Cambridge University Press.2007.
6 王世儒,等.计算方法[M].西安:西安电子科技大学出版社,1996.(Wang Shiru,et al.Calculation method[M].Xi’an:Xidian University Publishing House,1996)
7 徐萃薇,孙绳武.计算方法引论[M].北京:高等教育出版社,2002.(Xu Cuiwei and Sun Shengwu.Introduction to computational methods[M].Beijing:Higher Education Press,2002)
8 张守建,等.两种IGS精密星历插值方法的比较分析[J].大地测量与地球动力学,2007,(2):80-83.(Zhang Shoujian,et al.Comparative analysis on two methods for igs precise ephemeris interpolation[J].Journal of Geodesy and Geodynamics,2007,(2):80 -83)
9 邱蕾,廖远琴,花向红.基于IGS精密星历的卫星坐标插值[J].测绘工程,2008,17(4):15 - 18.(Qiu Lei,Liao Yuanqin and Hua Xianghong.Interpolation methods for precision ephemeris based on IGS[J].Engineering of Surveying and Mapping,2008,17(4):15 -18)
10 马俊,等.基于IGS精密星历的卫星位置内插方法比较[J].城市勘测,2011,5:89 - 93.(Ma Jun,et al.IGS precise ephemeris based on the comparison of the ways for the satellite position interpolation[J].Urban Geotechnical Investigation & Surveying,2011,5:89 -93)
11 何玉晶,杨力.基于拉格朗日插值方法的GPS IGS精密星历插值分析[J].测绘工程,2011,20(5):60- 62.(He Yujing and Yang Li.Analysis of interpolation results on GPS IGS precise ephemeris based on Lagrange interpolation[J].Engineering of Surveying and Mapping,2011,20(5):60-62)
COMPARISON ON INTERPOLATION METHOD FOR HIGH SAMPLING RATE OF GPS SATELLITE ORBIT
Wang Qingping,Chen Guang,Chen Chaoxian and Zhao Wenbo
(Earthquake Administration of Fujian Province,Fuzhou350003)
The computation and the accuracy and running time of Lagrange interpolation,Newton interpolation,Neville successive linear interpolation are compared.The result indicates that each algorithm is feasible within the required accuracy range,but it is easy to produce Runge phenomenon in Lagrange interpolation.Coefficients of the interpolating polynomial algorithm is about 45 times faster than Lagrange interpolation and 15 times faster than Newton and Neville interpolations at 50 Hz sampling rate interpolation experiments.
GPS precise ephemeris;Lagrange polynomial interpolation;Newton polynomial interpolation;Neville successive linear interpolation;polynomial coefficients solving method
P207
A
1671-5942(2013)05-0049-04
2013-02-09
福建省地震局青年科技基金(Y201201、Y201003);中国地震局地震科技星火计划项目(XH13011Y)
王青平,男,1984年生,博士,工程师,主要从事GPS形变监测研究.E-mail:wacs5@126.com

