信息系统下弹性需求随机用户均衡演化模型

度 巍，黄崇超，肖海燕，王先甲

(1.南通大学交通学院，江苏南通226019;2.武汉大学数学与统计学院，武汉430072;3.湖北第二师范学院数学与数量经济学院，武汉430205;4.武汉大学系统工程研究所，武汉430072)

1 引 言

交通网络流量作为研究交通问题的基本因素，其形成机理一直是交通规划学者的研究热点，交通流量分布可以看成是众多交通出行者长期相互博弈，选择出行线路及出行方式的结果［1，2］.近年来，由于先进交通信息系统ATIS(Advanced Traveler Information Systems)的普及，越来越多的学者考虑动态交通系统演化中，出行者在日常出行中的信息学习与更新过程，在宏观视角下刻画交通网络流分布的状态演化过程，以及在信息影响下用户均衡分布状态是否达到［3-7］.在实际交通出行中，不同出行者的时间价值(VOT)［3］、接受ATIS系统提供交通信息的程度往往不同，从而在建立模型时需要考虑将出行者分成不同类型，在文献［7，8］中，根据出行者接受交通信息的信任程度，将出行者分为保守与乐观两种类型，推导出总的期望路径出行费用.本文在此基础上，得到考虑弹性交通需求的随机用户均衡演化模型，分析了两种类型的出行者比例对交通流演化的影响，并在算例中进行了仿真实验，进一步验证了保守型出行者在总出行者中所占比例对交通流演化的影响结果.

2 基本交通网络描述

定义一般交通网络G=(N，A)，其中N为节点集合;A为有向路段的集合.定义a为G中任意一条路段;xa(t)为路段 a在 t时期的流量;Ta(xa(t))为路段a的出行费用函数;W为G中的OD对集合;w为W中的任意一条OD对;Pw表示属于w的所有路径集合;为t时期w的交通需求;p为属于Pw的任意一条路径(t)为属于w的路径p在t时期的流量;令(t)为t时期交通信息系统提供OD对w中路径p的客观路径出行费用;当路段a在OD对w中路径p上时为1，否则为0，则有

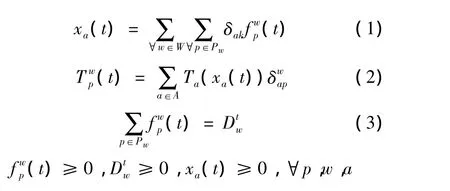
3 交通出行者期望路径费用更新机制

交通路网中的出行者路线选择过程是一个经验积累的过程，出行者会根据交通信息系统提供的交通状况信息和以往的经验调整自己的出行路线.本文假定交通路网中的所有出行者均能接受交通信息系统提供的路况信息，根据出行者对交通信息的信任和接受程度，将出行者分为信任乐观和保守两种类型.根据文献［7，8］中的表述，定义D0为初始时期的交通信息集合;Dt为t时期初的交通信息集合，假定交通信息就是该时期所能获得的各种路径出行费用数据.令为t时期对由交通信息系统提供的客观路径出行费用的感知值，作为随机变量.与之间的误差εt为t时期由各种交通状况所导致的波动，其期望为零，则有

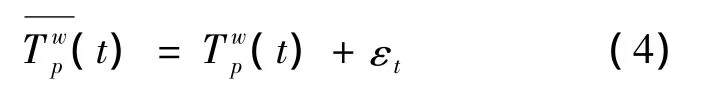
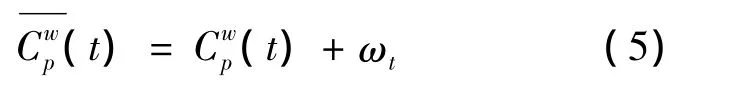
在t+1时期，交通信息集合Dt+1包括1)和时期的信任乐观者判断的路径费用为

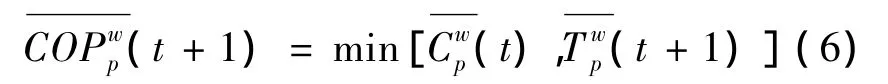
其对t+1时期路径费用的期望值为

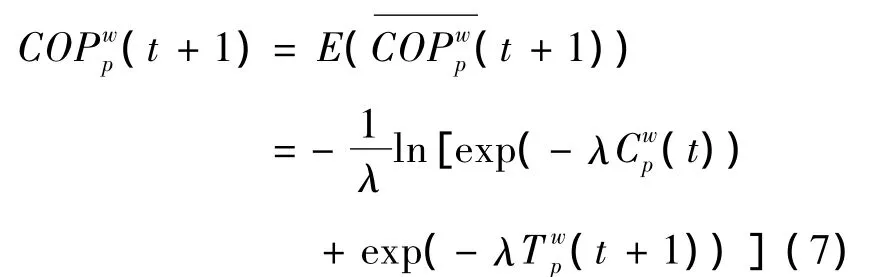
t+1时期保守者判断的路径费用为

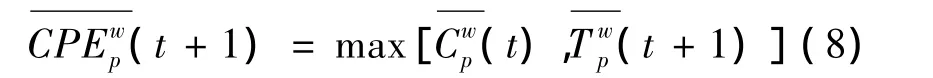
其对t+1时期路径费用的期望值为

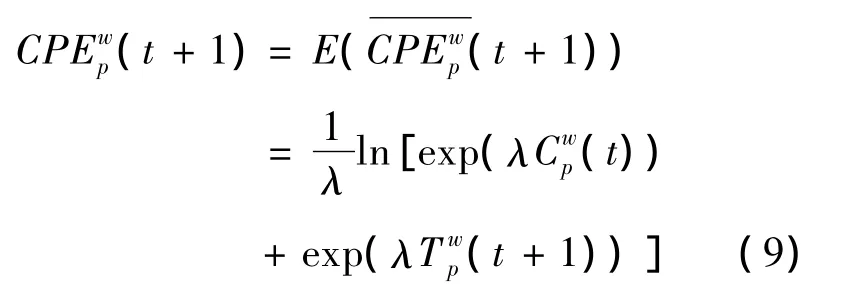
假设系统中没有既乐观又悲观的人，则全部出行者在t+1时期的期望理解路径出行费用为

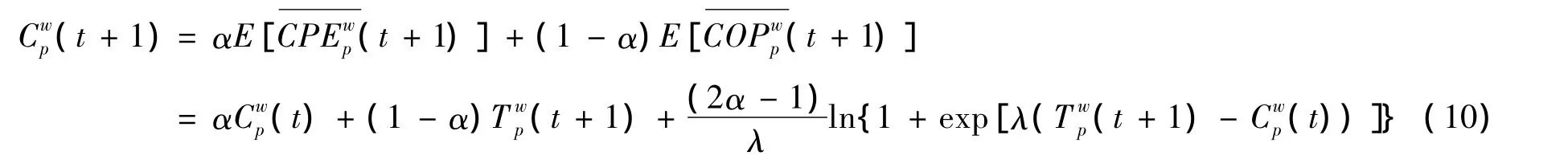
式中 α∈(0，1)表示保守者在总出行人数中的百分比，也可视为任意一个出行者对交通信息持怀疑保守态度的概率.

4 演化模型

当对路径费用感知误差不随时期改变时，根据离散选择理论，OD对w的路径p在t+1时期被选中的概率为

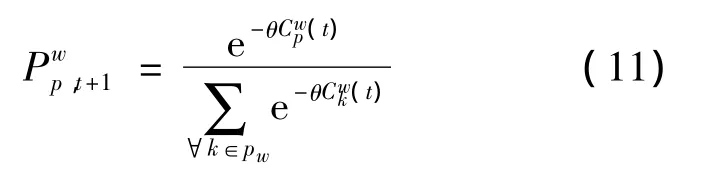
在随机用户配流中，各个路径被选中的概率和路径流量循环相依［9］.在最终的均衡状态下，各参量与时期t不再有关，有

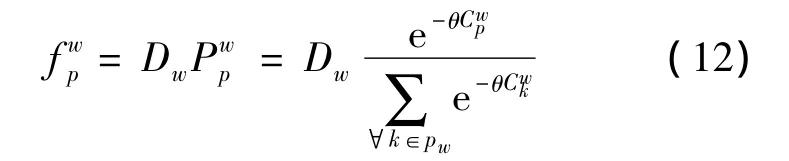
根据由刻画离散随机用户均衡状态的Logit动态［10］，路网流量演化到随机用户均衡的Logit动态方程为

由于在长期的交通流演化中，各个OD对的交通需求量与出行费用存在相互作用，因此在模型中考虑需求弹性更为合理，此时有

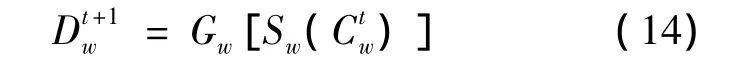
5 保守型出行者比例对演化模型的影响

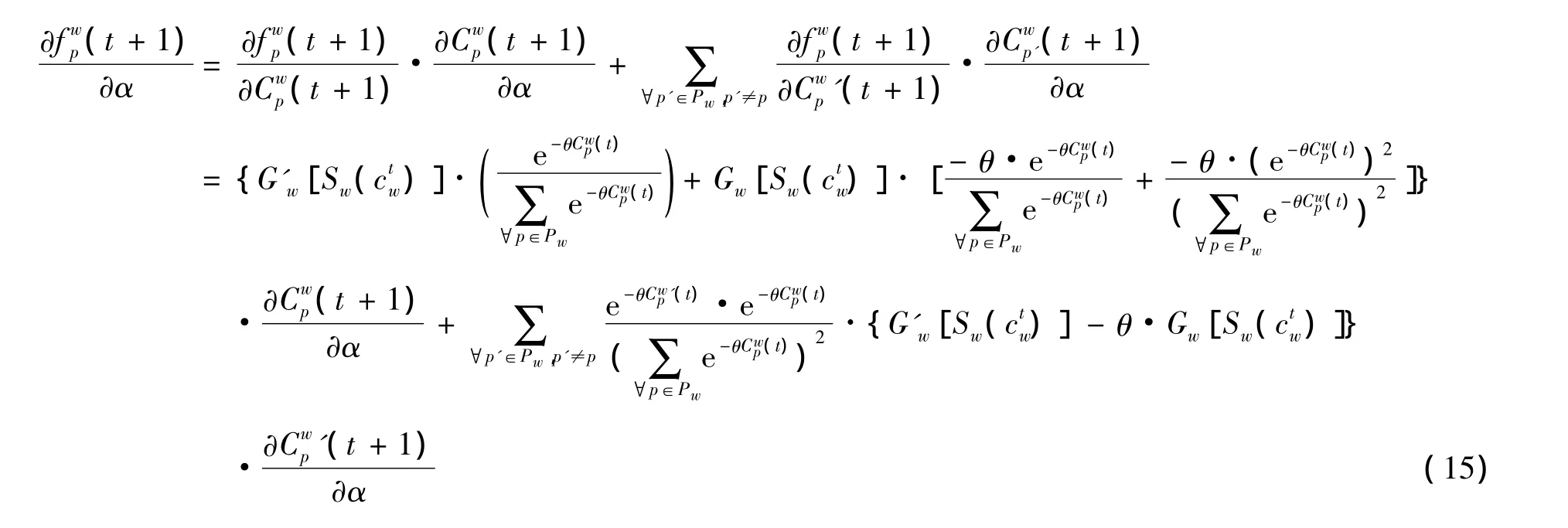
根据Gw(·)是单调递减函数知＜0，分析式(15)知，即随着保守者比例的增加，各个OD对路径流量将减少，下面通过一个算例进一步验证分析的结论.

6 数值试验

本文采用文献［2］中的网络进行交通信息作用下的弹性需求随机用户均衡演化仿真.如图1所示，网络有13个节点，19个路段，4个OD对和25个路径，弹性需求函数采用指数形式 ，即为各个OD对的最大交通需求量，四个OD对的最大需求量设为［1 200 900 1 100 1 000］，参数βw的值分别为［0.02 0.022 0.019 0.018］.

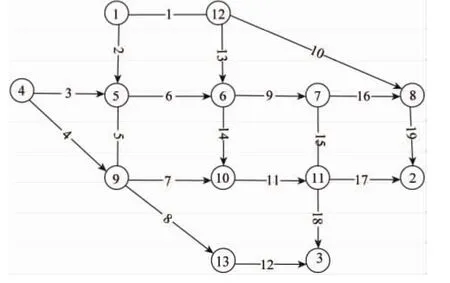
图1 算例网络Fig.1 Example network

仿真中路段费用函数设为

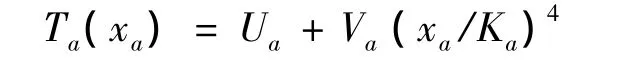
式中 参数Ua是路段 a的自由流时间，Va＞0，Ka＞0.图1中各个路段对应的参数值如表1所示.

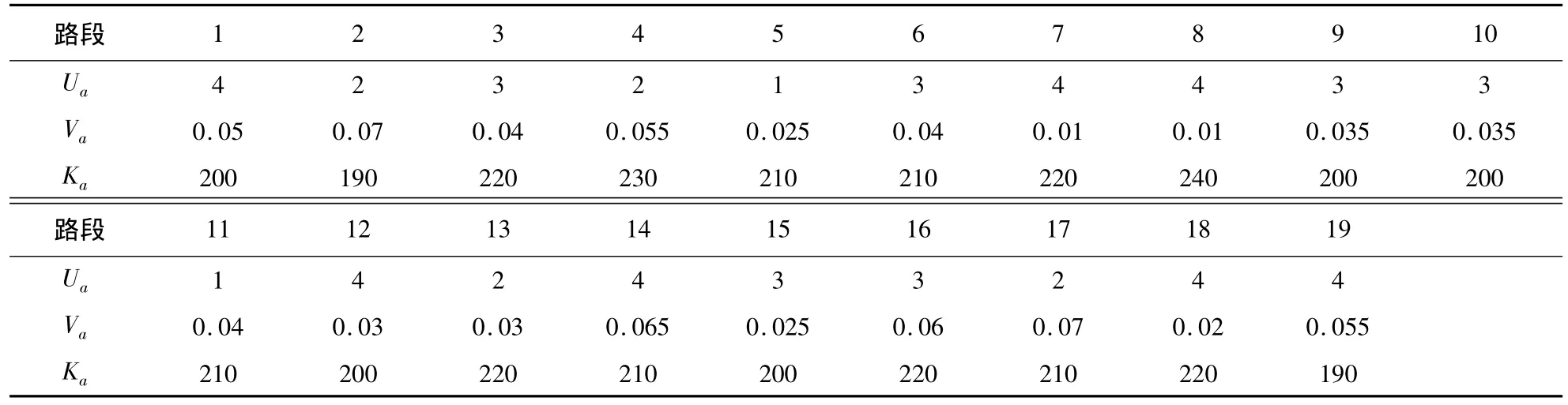
表1 路段费用函数的参数Table 1 Parameters of the link performance fuctions

取迭代次数为50，各个路径的初始流量均为20，参数λ设置为0.437 9，θ设置为0.3.数值试验结果表明对于任意的α∈(0，1)，交通流均能收敛到弹性需求下的随机用户均衡状态，图2-图5分别给出了当α设置为0.2和0.8时，各OD对路径费用和流量的演化过程.表2、表3给出了两种取值下对应的最终均衡状态下的具体路径费用和流量值.

当α的取值从0.2向0.8变化过程中，图6、图7给出在α不同取值下，演化均衡状态的路径费用和流量的变化情况.

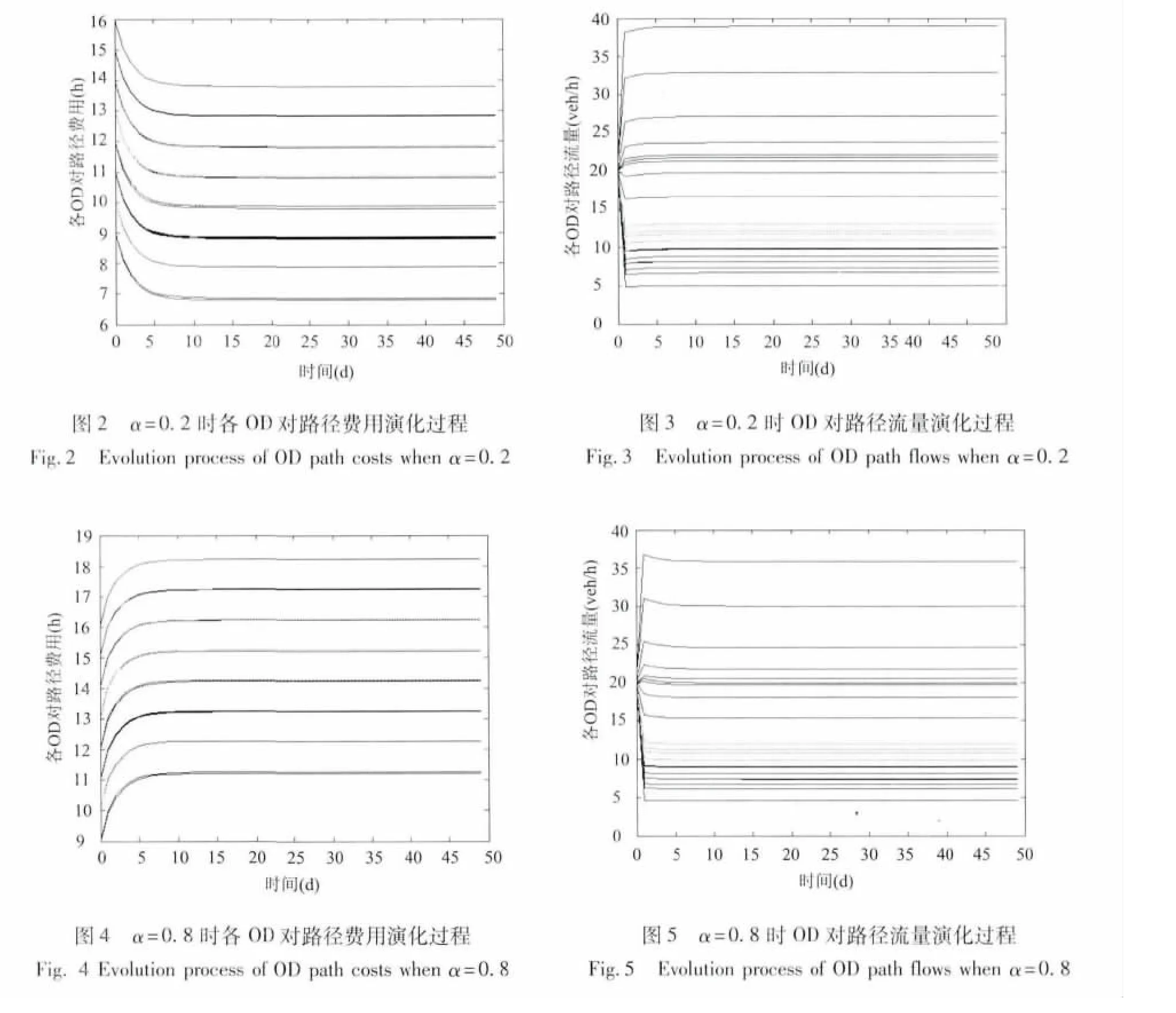
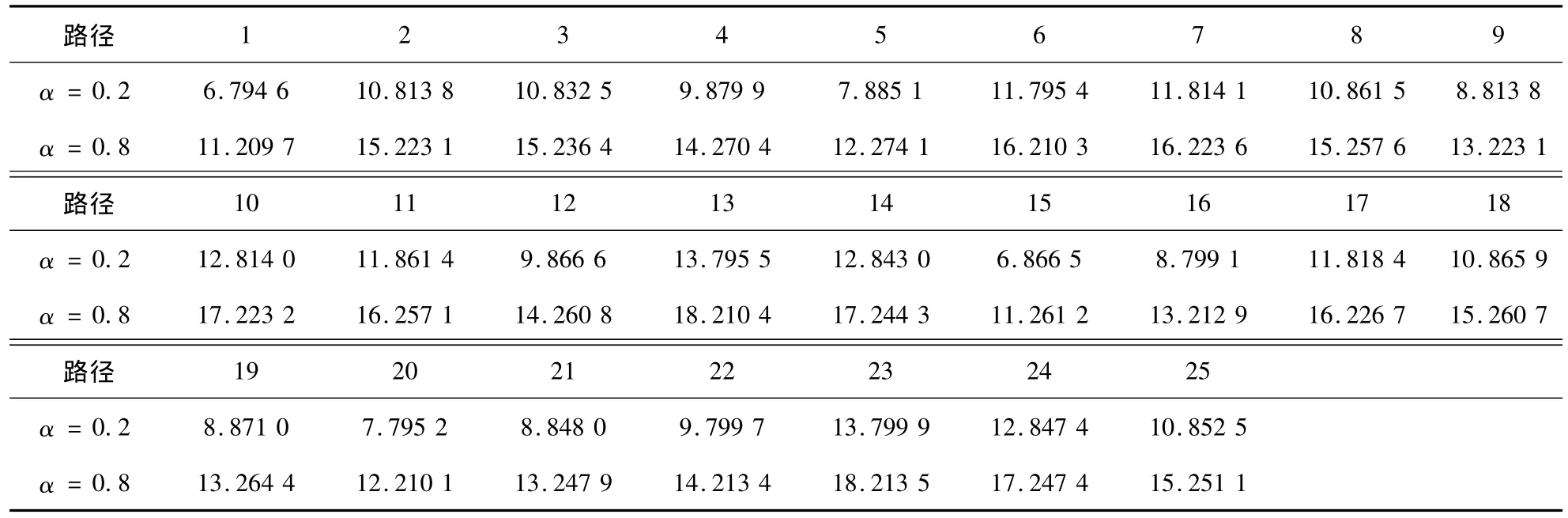
表2 各OD对路径费用值Table 2 Equalization OD path costs

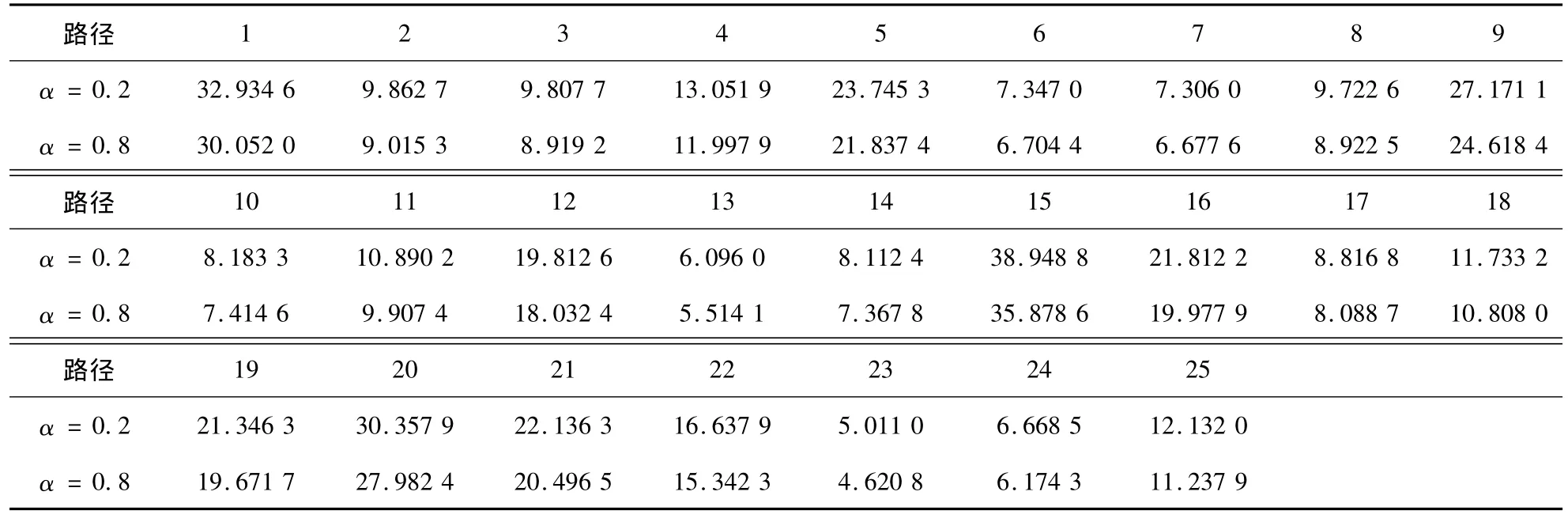
表3 各OD对路径流量值Table 3 Equalization OD path flow

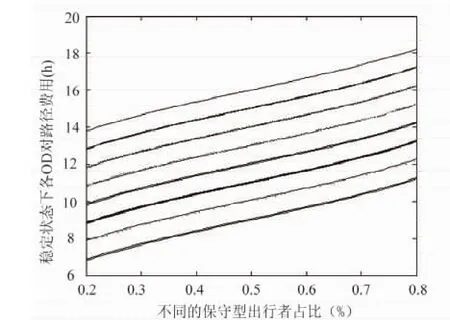
图6 不同保守型出行者占比下各OD对路径均衡费用Fig.6 OD path costs in different α

从算例仿真结果可以看出，当保守型出行者在出行人群中所占比例较小和较大时，交通流均能朝着Logit动态的零点即随机用户均衡态发展，而随着保守型出行者比例系数α的增大，各OD对路径均衡费用均单调递增，各OD对路径均衡流量均单调递减，进一步验证了对模型分析结论.

7 研究结论

本文通过考虑出行者对于ATIS提供的路网信息的接受程度，将出行者分成乐观和保守两种类型，在相应得出的各条交通路径出行费用的基础上，建立起弹性需求随机用户均衡演化模型，并通过算例仿真，得出网络交通流在该模型下的演化轨迹.从仿真结果可以看出，保守型出行者比例较大时交通流流量减小，而运行费用增大，这显然与降低交通运行费用、提高城市交通网络利用效率的管理原则相悖.从而在普及ATIS系统的过程中，要提高ATIS的信赖度，使更多的出行者相信ATIS提供的交通信息，愿意服从ATIS引导出行，促使保守型出行者逐渐改变习惯，朝乐观型出行者转变，减少保守型出行者的比例，有利于改善ATLS的使用效果，促进网络交通流的稳定.本文对交通部门分析ATIS对交通流的影响，以及进一步采取各种管理控制措施具有一定程度的指导意义.

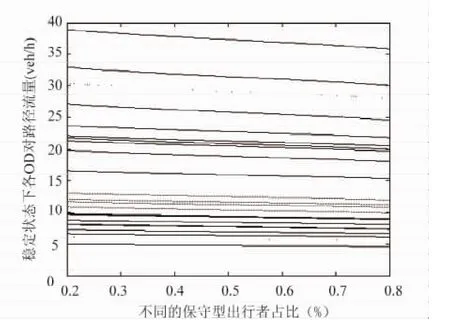
图7 不同保守型出行者占比下各OD对路径均衡流量Fig.7 OD path flows in different α

［1］郭仁拥，黄海军.ATIS环境下交通配流的动态演化模型［J］.管理科学学报，2008，11(2):12-19.［GUO R Y，HUANG H J.Dynamical evolutionary model of traffic assignment under ATIS［J］.Journal of Management Sciences in China，2008，11(2):12-19.］

［2］Guo R Y，Huang Hai-Jun.Chaos and bifurcation in dynamical evolution process of traffic assignment with flow mutation［J］.Chaos Solitons＆ Fractals，2009，41(3):1150-1157.

［3］郭仁拥，黄海军.基于ATIS的多用户多准则随机均衡交通配流演化模型［J］.中国公路学报，2008，21(5):87-90.［GUO R Y，HUANG H J.Evolution modelof multiclass and multicriteria stochastic equilibrium traffic assignment based on ATIS［J］.China Journal of Highway and Transport，2008，21(5):87-90.］

［4］Huang Hai-Jun，Lam W H K.A multi-class dynamic user equilibrium model for queuing networks with advanced traveler information systems［J］.Journal of Mathematical Modeling and Algorithms，2003，2(4):349-377.

［5］Lo H，Szeto W Y.Modeling advanced travller information services:State versus dynamic paradigms［J］.Transportation Research B，2004，38(6):495-515.

［6］Huang Hai-Jun，Liu Tian-Liang，Yang Hai.Modeling the evolutions of day-to-day route choice and year-toyear ATIS adoption with stochastic user equilibrium［J］.Journal of Advanced Transportation，2008，42(2):111-127.

［7］Toshihiko Miyagi.The stability of stochastic user equilibrium with a given set of route information［M］.Transportation Network: Recent Methodological Advances，Elsevier Science，1998.

［8］熊轶，黄海军，李志纯.交通信息系统作用下的随机用户均衡模型与演进［J］.交通运输系统工程与信息，2003，3(1):28-32.［XIONG Y，HUANG H J，LI Z C.A stochastic user equilibrium model under ATIS and its evolutionary implementation［J］.Journal of Transportation Systems Engineering and Information Technology，2003，3(1):28-32.］

［9］周晶.随机交通均衡配流模型及其等价的变分不等式问题［J］.系统科学与数学，2003，23(1):120-127. ［ZHOU J. Stochastic user equilibrium assignmentmodelwith its equivalentvariational inequality problem［J］.Journal of Systems Science and Mathematical Science，2003，23(1):120-127.］

［10］Yang F.An evolutionary game theory approach to the day-to-day traffic dynamics［D］. Dissertation:University of Wisconsim-Madision，2005.