考虑列车容量的轨道交通客流分配模型

朱宇婷，毛保华*，李明高，甘恬甜，赵宇刚

(1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044;2.铁道部经济规划研究院，北京100038)

1 引 言

客流不仅是规划轨道交通网络、安排工程项目建设顺序、设计车站规模和选择车站设备容量的依据，也是轨道交通系统合理安排行车组织的基础.目前，国内外的专家学者在城市道路交通网络流量分配方面取得了大量研究成果.然而，轨道交通网络与道路交通网络的流量分配有着明显的不同，其不仅要考虑起讫点间的运行时间，还要考虑站台等待时间(包括因车辆满载而造成的滞留等待时间).部分学者采用罚函数近似替代列车容量，间接计算乘客等待时间［1，2］;部分学者采用有效服务频率近似计算乘客等待时间［3，4］;还有部分学者采用未上车概率反映乘客滞留现象［5-7］.上述方法都是基于频率的静态客流分配方法，虽然能够在一定程度上反映轨道交通拥挤现象，但依旧难以准确描述每趟车的满载情况.

面对这一问题，Tian［8］建立了多起点单讫点的高峰期公交均衡模型，并研究了不同站点地理位置的差异对高峰流量分布的影响;Hamdouch［9］采用改进的时间扩展网络描述公共交通网络，提出了考虑列车容量的客流分配模型.上述文献虽然能够严格控制每辆车的满载情况，较为真实地重现乘客选择行为，但一些关键问题还没有得到很好地解决，如乘客站台滞留过程，拥挤状态下各站乘客到达规律，以及服务水平对客流分布的影响等.

本文对轨道交通网络的客流分配问题进行了理论建模，构建了基于时刻表的拟动态分配模型，并设计了求解算法.最后，采用了一个多起点单讫点的轨道交通线路对模型及算法进行了验证.

2 网络描述及基本假设

2.1 问题描述

考虑有一条轨道交通线路由始发站Oa出发，经Ob…Ok等站开往工作区W，如图1所示.每天早晨分别有qa、qb…qk个乘客从各站上车去W上班.

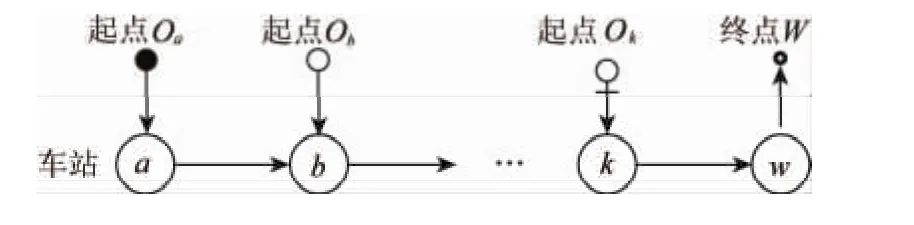
图1 多起点单讫点城市轨道交通网络示意图Fig.1 A route network with many-to-one mass transit system

根据国内外轨道交通运营实践，不失一般性，做出如下假设:

(1)所有列车的编组辆数一致，即列车具有相同的载客能力，用N0表示列车最大载客量，当某一班次列车达到最大容量，则该站剩余乘客将不能搭乘该班列车，需要排队等待下一次列车，从而产生车站滞留时间.

(2)列车运行速度恒定，即所有列车在同一区间具有相同的运行时间.

(3)所有出行者具有相同属性，即有相同的上班时间，相同的时间价值及相同的拥挤敏感度，且出行者对轨道交通的发车时间具有完全信息.

(4)轨道交通严格按照列车时刻表运行，根据到达工作地W的先后顺序对各班次进行编号:Γ ={…，-2，-1，0，1，2，…}，其中 0 表示唯一能够准时到达的列车.

(5)不考虑乘客在起讫点发生的站外消耗时间.

2.2 时间拓展网络

任何一条轨道交通都拥有既定的运行方案，为准确描述这一信息，本文采用列车班次代替具体时间，对既有网络图进行时间拓展，生成单线轨道交通时间拓展网络，从而将乘客出行时间选择问题转化成为路径选择问题，如图2所示.

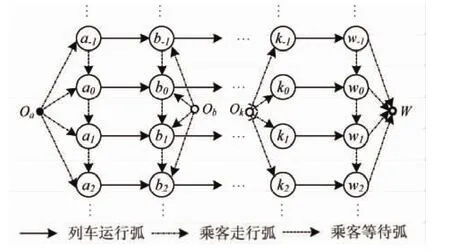
图2 图1的时间拓展网络示意图Fig.2 The time-expanded network of the route network in Fig.1

用赋权有向图G=(O，W，N，A)表示该拓展网络图.O为乘客居住地集合;W为工作区;N为带时间属性的车站节点集，即每个车站i被拓展成为多个分节点iτ(τ∈Γ);A为弧集合.

为方便描述，首先定义数学符号如下:

cij—— 节点i和j的时间差，当i≠j，i∈N 时，cij表示列车运行，当i=j，i∈N时，cij表示乘客滞留等待时间，当i∈O或j∈W时，cij表示起、终点站乘客站外消耗时间，根据假设5，取其值为0;

s——乘客出发时刻，其与列车班次相对应，即选择乘坐该班次列车出发的乘客，其出发时刻s=τ;

S——乘客出发时刻集合(∀s=S)，用“出发时刻数”表示该集合元素的个数;

fij(X)—— 进入弧(i，j)的乘客数;

gij(fij(X))——弧(i，j)上产生的拥挤费用，令gij(fij(X))=0.05fij(X);

Δτ——第τ次列车与第0次列车的发车时间差;

pij——到达终点时乘客所承担的迟到/早到惩罚，当且仅当j∈W时，该费用发生，假设节点i所带时间属性值为 τ，则有 pij=

β——早到时间惩罚;

γ——迟到时间惩罚;

α——时间价值系数.

3 轨道交通客流分配模型

乘客选择路径ρ的出行成本主要包含:路径出行时间、站台滞留等待时间、票价及出行惩罚(迟到/早到惩罚、拥挤惩罚等).其表达式为

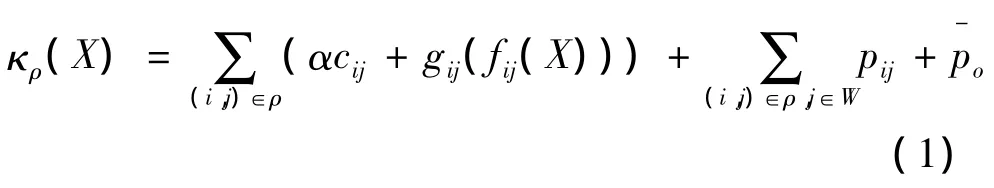
由于列车最大载客量的存在，各出发时刻将对应多个可能的径路，即s时刻从起点O出发的乘客进入路径ρ的概率为［10］

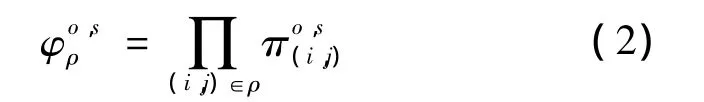
则s时刻从起点O出发乘客的出行总成本为

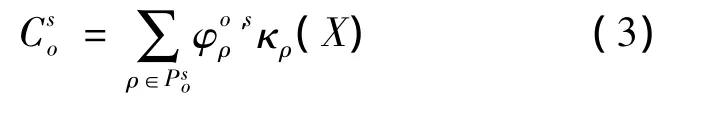
轨道交通网络的客流分布是一种相互反馈的动态平衡机制.根据Wardrop第一原理，轨道交通网络客流分布的平衡状态可描述为:在OD之间所有可供选择的路径中，乘客所选择的各条路径上的广义费用期望值全都相等，且不大于未被选择路径的广义费用期望值.即寻找X*满足以下变分不等式［11，12］:

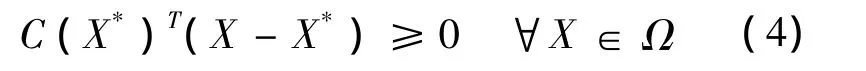
式中 C(X)表示流量分配向量X对应的费用向量.

本文采用MSA算法求解城市轨道交通网络客流分配问题.具体步骤如下:

Step 1 令 X［0］=0，计算 C(X［0］)，得到每个OD 对 (q，r)的初始出发时刻s*［1］，令k=k+1，赋值=d(q，r)，得到向量X［1］.

Step 2 计算C(X［k］).重新选择各OD对的最优出发时刻s*［k］，并赋值

4 数值试验

4.1 算例

我们选用一个拥有7站点的简单网络进行实验，如图3所示，横线上的数字为运营时间(单位:h).输入参数如下:α=20元/h，β=10元/h，γ=30元/h，列车均匀发车，发车间隔H=0.1h，各站出行需求均为900人，列车最大容量为330人.图4为各站乘客到达分布情况.

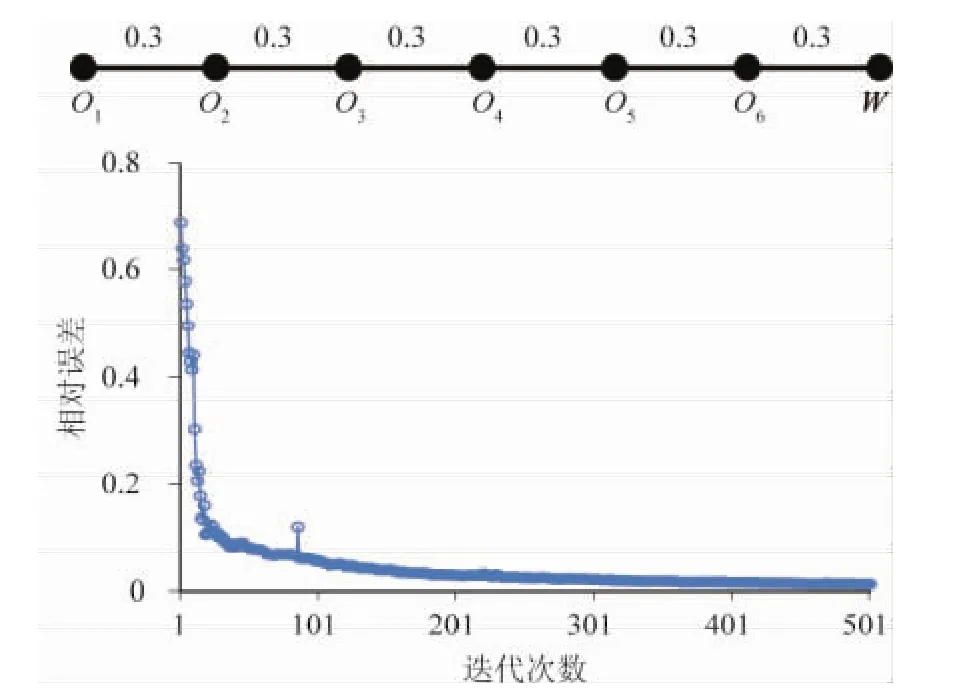
图3 单线网络及收敛结果图Fig.3 Single line network and convergence result

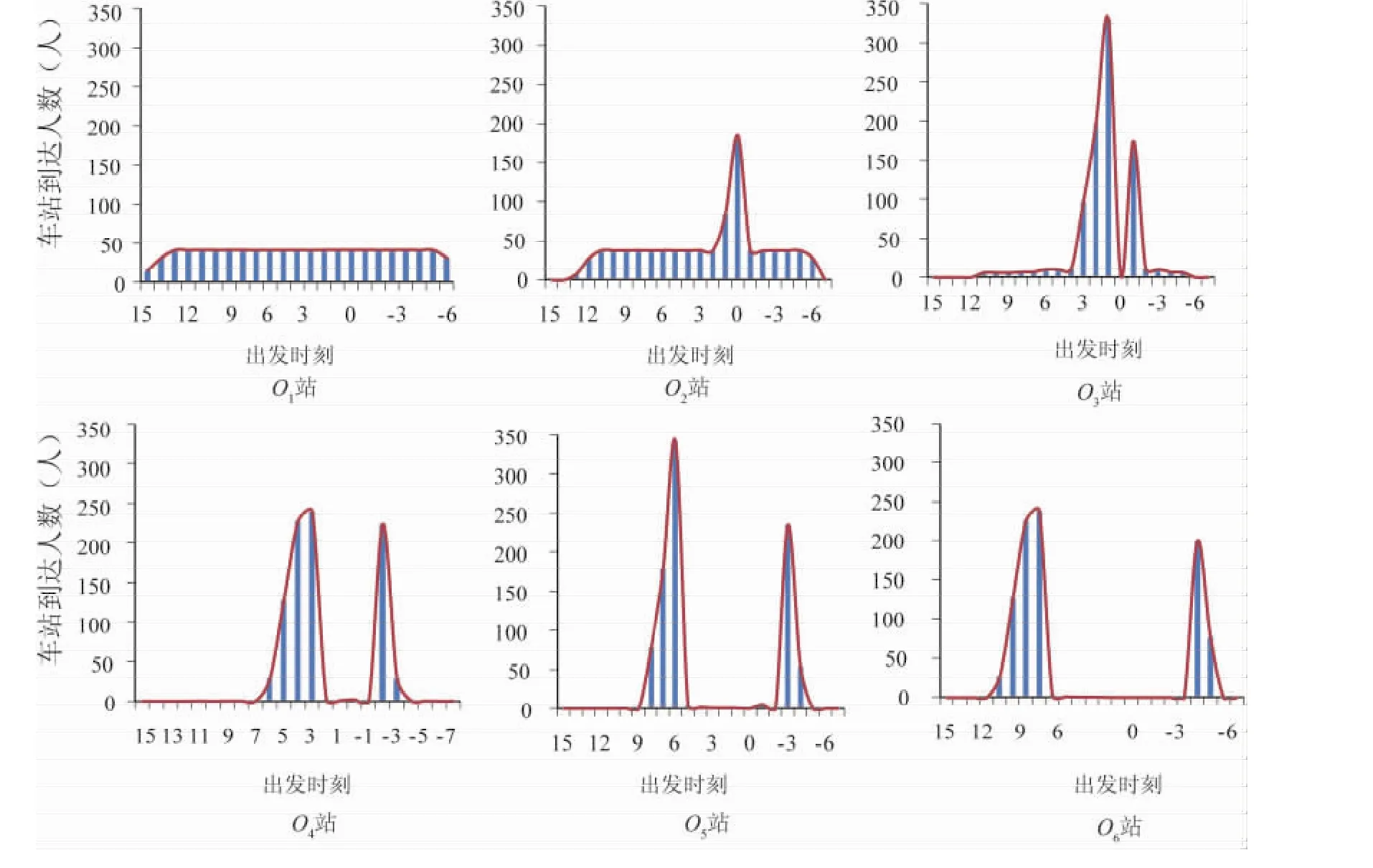
图4 各站乘客到达分布图Fig.4 The distribution of passenge in each station

从图4可以发现，单线轨道交通客流到达分布规律主要可分为三种类型:

①双峰型.该类客流到达规律出现在O3、O4、O5、O6四个车站，受列车容量的限制，这些车站上的乘客乘坐准点列车的机会较小，他们必须在早到与晚到中做出选择，从而在分布规律上呈现出2个明显的波峰，且随着车站与终点距离的缩短，波峰间的距离增大.

②单峰型.该类客流到达规律出现在O2站，该站乘客虽未直接面对满员列车，但受后续4个车站的影响，非正点列车的拥挤度产生了不同程度的提高，对乘客的吸引力减弱，从而在第0时刻周围形成客流高峰.

③均峰型.该类客流到达规律出现在O1站，该站乘客不仅不受列车容量的影响，且在O2站乘客的调节下，所能感知到的列车拥挤度也没有产生明显变化，因此，其在时间上没有明显的高峰时段，客流到达满足Tian［8］中提到的均衡现象.

4.2 灵敏度分析

由于模型和算法中涉及变量较多，这些数据作为已知条件，对乘客出行选择行为会产生影响.为了更好地把握乘客出行选择行为的变化规律，本节将针对服务水平(列车发车间隔及列车容量两部分)进行灵敏度分析.不同服务水平下的客流分配结果如图5、图6所示.

从图5、图6可以得到以下结论:

(1)随着服务水平的提高，客流分布由双峰型向单峰型，最后再向均峰型过渡，且越靠近始发站起点的车站越早进入均峰期，越靠近终到站的车站越晚离开双峰期，这说明越靠近终到站的车站越先摆脱列车容量的干扰.

(2)随着列车容量的提高，各站乘客的出发时刻数逐步脱离双峰期的稳定状态，并在单峰期呈现逐步上升的趋势，最后在均峰期再次出行稳定值.这说明乘客的拥挤感知与遭遇满载列车的概率呈反比，当在站乘客确实遭遇满载列车时，拥挤成本对乘客出行选择行为的影响几乎没有，出行行为集中在较为准时的几趟车上.

(3)随着发车间隔的减小，均峰期乘客出发时刻数增大，这说明乘客的拥挤感知强度与服务水平成正比，服务水平越高，乘客对拥挤成本越敏感.

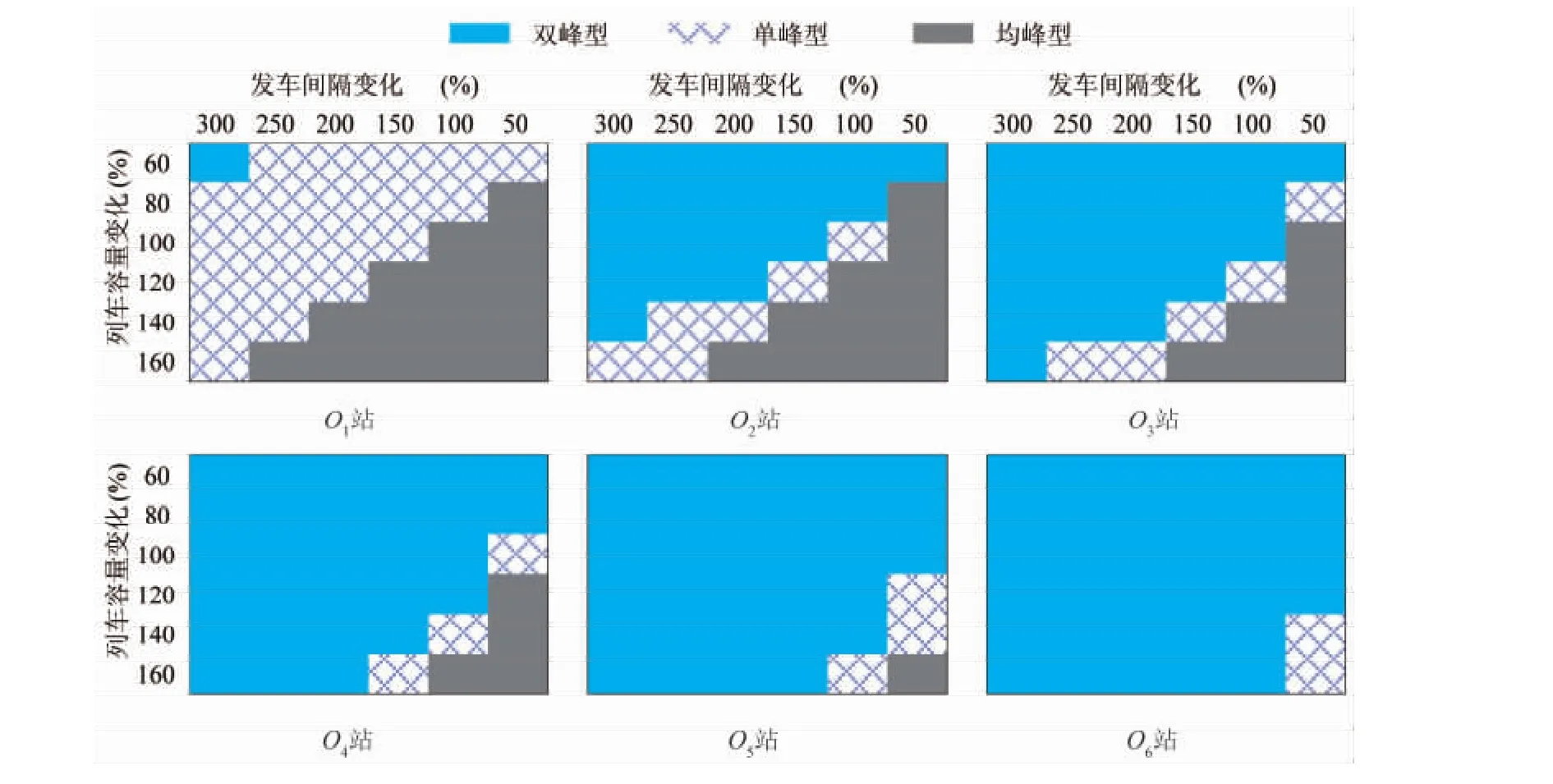
图5 各站客流到达规律变化Fig.5 Thevariation of flow distribution in each station

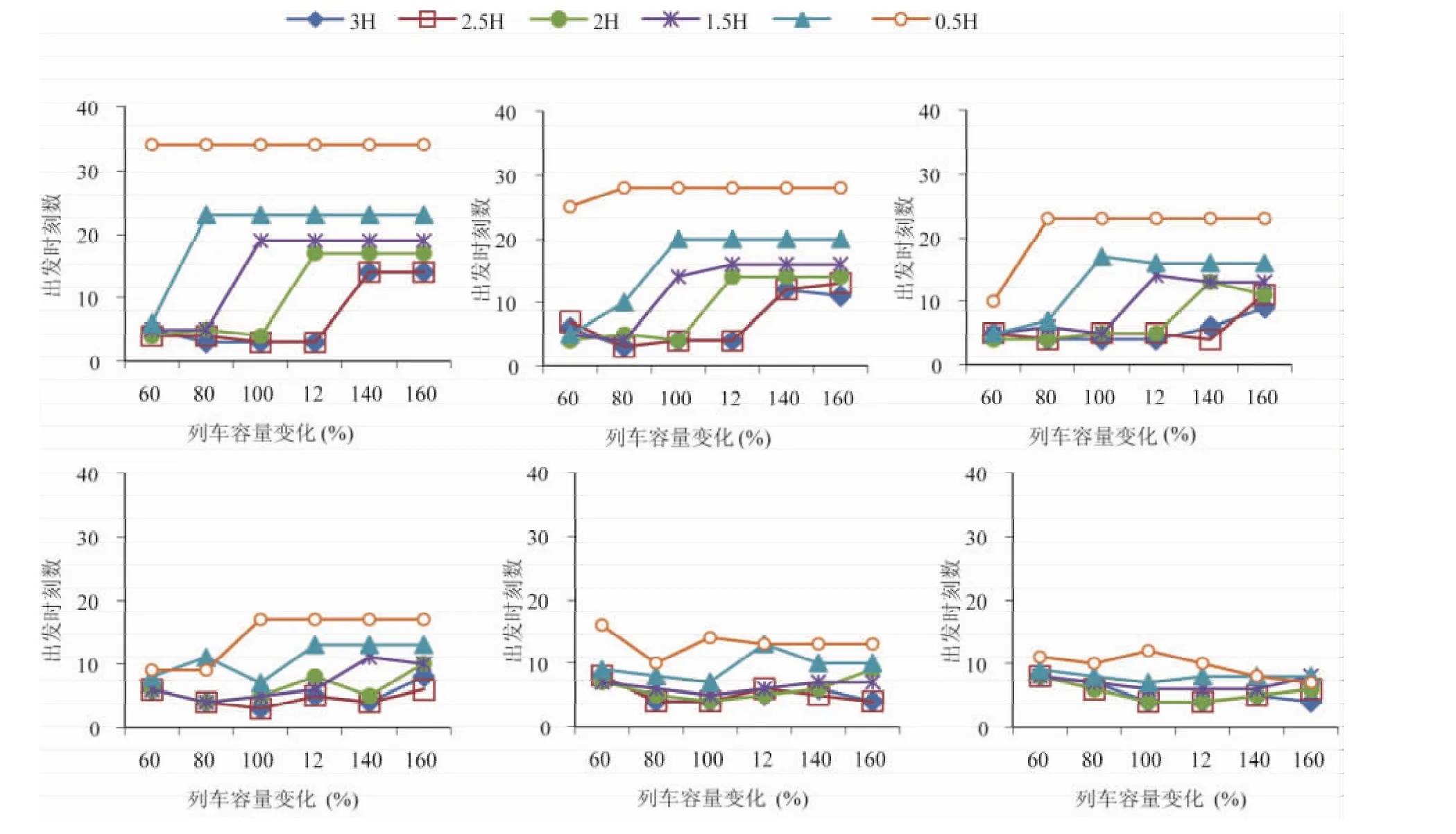
图6 各站乘客出发时刻数变化Fig.6 The variation of the number passengers’departure time in each station

(4)随着车站与终点距离的缩小，均峰期乘客出发时刻数减小，即各站均峰期出发时刻数由多至少依次为:O1、O2、O3、O4、O5、O6.这说明随着旅行时间的增加，乘客对拥挤越发敏感，这一结果与Alfa和Tian相一致.

5 研究结论

本文提出了一种基于时间拓扑网络的轨道交通拟动态客流分配模型，将乘客出行时间选择问题转化成路径选择问题.该模型假设所有乘客具有相同的属性，且按照先到先服务的原则进入轨道交通网络;通过设定连接弧的通过能力，对各次列车的满载率进行控制;能够较好地反映各站乘客间序贯博弈的特性.

为验证模型的有效性，本文选用了一个7个站点的城市轨道交通线网进行数值试验.实验结果表明，单线轨道交通客流到达规律主要呈现出双峰型、单峰型和均峰型三种类型，且随着服务水平的提高，乘客对拥挤成本越发敏感，出发时刻数逐渐增加，客流到达分布规律向均峰型变化.本研究并未考虑弹性需求方面的问题，这也是作者下一步研究的重点.

［1］Lam W H K，Gao Z Y，Chan K S，et al.A stochastic user equilibrium assignment model for congested transit networks［J］. Transportation Research PartB:Methodological，1999，33(5):351-368.

［2］Nguyen S，Pallottino S，Malucelli F.A modeling framework for passenger assignment on a transport network with timetables［J］.Transportation Science，2001，35(3):238-249.

［3］四兵锋，毛保华，刘智丽.无缝换乘条件下城市轨道交通网络客流分配模型及算法［J］.铁道学报，2007，29(6):12-18.［SI B F，MAO B H，LIU Z L.Passenger flow assignment model and algorithm for urban railway traffic network under the condition of aeamless transfer［J］.Journal of the China Railway Society，2007，29(6):12-18.］

［4］Cepeda M，Cominetti R，Florian M.A frequency-based assignment model for congested transit networks with strict capacity constraints:characterization and computation of equilibria［J］.Transportation Research Part B:Methodological，2006，40(6):437-459.

［5］Schmöcker J D，Bell M G H，Kurauchi F.A quasidynamic capacity constrained frequency-based transit assignment model［J］.Transportation Research Part B:Methodological，2008，42(10):925-945.

［6］Kurauchi F，Bell M G H，Schmöcker J D.Capacity constrained transit assignment with common lines［J］.Journal of Mathematical Modelling and Algorithms，2003，2(4):309-327.

［7］田琼，黄海军.一个考虑早到惩罚的高峰期地铁乘车均衡模型［J］.交通运输系统工程与信息，2004，4(4):108-112.［TIAN Q，HUANG H J.An equilibrium ride model for subway passengers with arrival early penalty［J］.Journal of Transportation SystemsEngineering and Information Technology，2004，4(4):108-112.］

［8］Tian Q，Huang H J，Yang H.Equilibrium properties of the morning peak-period commuting in a many-toone mass transit system［J］.Transportation Research Part B:Methodological，2007，41(6):616-631.

［9］Hamdouch Y，Marcotte P，Nguyen S.A strategic model for dynamic traffic assignment［J］.Networks and Spatial Economics，2004，4:291–315.

［10］Spiess H，Florian M.Optimal strategies:a new assignment modelfor transitnetworks［J］. Transportation Research Part B:Methodological，1989，23(2):83-102.

［11］Dafermos S.Traffic equilibrium and variational inequalities［J］.Transportation Science，1980，14(1):42-54.

［12］Smith M J.The existence，uniqueness and stability of traffic equilibria［J］.Transportation Research Part B:Methodological，1979，13(4):295-304.