基于K-近邻的自由飞行冲突探测研究

赵元棣，孙 禾，王洁宁

(中国民航大学a.天津市空管运行规划与安全技术重点实验室;b.空中交通管理研究基地，天津 300300)

1 引 言

随着空中交通需求的不断增加，导致空域资源紧张，空中交通异常拥挤，为民航业的发展带来了巨大的挑战.为解决此问题，美国人威廉·克顿在1965年首次提出了“自由飞行”的概念，并在近些年受到越来越多的重视.美国航空无线电委员会(Radio Technical Commission for Aeronautics，RTCA)在1995年给出了“自由飞行”的定义［1］:自由飞行是在仪表飞行规则下的一种安全有效的飞行体系.在该体系中，飞行员可以更加灵活地选择适合自己的航路和速度.

在自由飞行的条件下，航空器的飞行距离大幅度减少，不仅为航空公司节约了燃油消耗，还可以提高空域的利用率.与此同时，自由飞行也必然导致管制员的工作负荷增大.飞行航路和速度的不确定性使得管制员难以像固定航路飞行那样事先判断航空器之间是否存在冲突，只能通过实时计算航空器之间的距离来进行冲突探测.因此，研究自由飞行条件下的冲突探测问题对于保障飞行安全、提高运行效率起到了至关重要的作用［2］.近些年，国内外已经有许多学者对此问题进行了研究，并取得了一些成果.Alliot等［3］讨论了如何利用遗传算法来解决空中交通管制中的冲突探测与解脱问题;Krozel等［4］采用最优控制理论提出了一种针对两架航空器在自由飞行条件下的冲突探测与解脱方法;Versteegt等［5］将动态密度的概念引入冲突探测与解脱的研究领域，并提出了航空器冲突解脱次数最少(Minimised number of Aircraft Solve Conflicts，MASC)的方法.在国内，靳学梅［6］针对两架航空器的冲突探测问题，使用矢量法构建了基于距离探测和时间探测的数学模型，并以此为基础进一步提出了针对多架航空器的冲突探测方法，用实例进行了仿真验证.程丽媛［7］在靳学梅的研究基础上，以航空器的质心空间运动轨迹为模型，对多架航空器之间冲突群的探测进行研究，并建立了数学模型.刘星等［8］应用遗传算法有效地解决了自由飞行条件下的飞行冲突探测与解脱问题，并且能尽量使航线接近理论上最省油的直线航线.

刘星等［9］和刘昕［10］均考虑到民用航空器在大部分时间内都是在固定高度飞行，从而将三维立体问题简化为二维平面问题，应用二维Delaunay剖分方法从数据处理效率角度对自由飞行冲突探测问题进行了研究.本文试图将航空器的飞行冲突探测问题推广到三维空间中进行研究，然而三维Delaunay剖分方法具有计算复杂度高、易退化、对于非均匀分布数据较敏感等缺点，并不适合于本文研究内容［9］.航空器在自由飞行条件下会呈现出位置不易确定、数量规模动态变化等特点，对于冲突探测方法的计算效率和稳定性的要求较高.本文将计算几何中的K-近邻方法引入自由飞行冲突探测问题，可以实时、快速、准确地计算出每架航空器与其距离最近的K架航空器之间是否存在冲突，并通过仿真实验证明了本文方法的有效性和鲁棒性.

2 K-近邻方法

K-近邻(K-Nearest Neighbor，KNN)方法最早是由Cover和Hart在1967年首次提出的一种非参数分类方法［11］.由于其具有简单直观、易于实现、对数据的噪声和采样密度不敏感等优点，现已成为数据挖掘和机器学习中的经典方法之一.K-近邻方法在原理上依赖于极限定理，其基本思想是:对于已知对象x，在度量空间内搜索距离x最近的K个目标对象，若这K个近邻大多数属于某一类别，则x也属于该类别.当K趋于无穷大时，K-近邻方法逼近于 Bayes最优分类方法［12］.由于 K-近邻方法兼顾了计算效率与稳定性，特别适合于在动态环境下连续搜索K个距离最近的目标对象，因此目前已被广泛应用于模式识别［13，14］、文本分类［15，16］、交通流预测［17］等领域.

由于本文所研究的冲突探测问题是假定在自由飞行条件下进行的，航空器的数量及其空间位置均呈现出动态不确定性，需要冲突探测方法具有较高的计算效率和较强的稳定性.本文利用兼备这两种特点的K-近邻方法较好地解决了自由飞行条件下的冲突探测问题.设三维空间点集为P={P1，…，Pn}，对于其中每一点Pi，计算与其欧氏距离最近的K个点Pi，1，…，Pi，K，称为Pi的 K-近邻，图1所示为K=5时的情况.

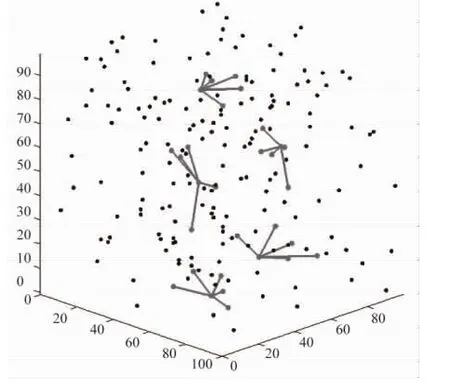
图1 三维点集K-近邻Fig.1 KNN of 3D point set

3 基于K-近邻的冲突探测方法

3.1 基本思想

假设在某指定空域内，所有航空器在某时刻的空间位置坐标构成三维空间点集P，本文利用其中每个点的K-近邻对未来一段时间内的冲突及潜在冲突进行快速、有效地探测.其基本思想是:将二次雷达实时获得的航空器空间位置坐标按照不同时段存储起来，并计算各时段内每架航空器的K-近邻，根据冲突判定规则搜索每架航空器与其K-近邻之间的距离即可判断当前时段内是否存在冲突或潜在冲突.

这种方法避免了对整个空域内的每对航空器进行距离探测，只需探测每架航空器与其周围的有限架航空器之间的距离是否满足冲突判定规则，从而大幅度节省了计算时间.此外，在不同时段内，当空域内的部分航空器位置发生改变时，无需针对整个空域内所有航空器进行距离数据更新，只需更新与其相关联的航空器的距离信息即可，在提高冲突探测效率的同时，增加了算法的可延续性.

3.2 方法描述

基于K-近邻的思想，本文方法的具体步骤如下:

(1)在某时段内，利用二次雷达记录整个空域内所有航空器的空间位置坐标，生成三维空间点集P={P1，…，Pn}，其中Pi=(xi，yi，zi)，i=1，…，n.

(2)对每一个点Pi∈P，计算与其欧式距离最近的K个点Pi，1，…，Pi，K∈P，并根据距离按照升序排列.当对P中的所有点均完成上述K-近邻计算后，即可通过全部欧式距离生成一个n×K维的距离矩阵D={dij}，其中第i行第j列元素dij表示第i架航空器与距其第j位近的航空器之间的欧氏距离.

(3)根据事先给定的冲突判定规则，将其中所定义的冲突间隔与潜在冲突间隔作为阈值，搜索距离矩阵D中所有满足上述规则的距离，进而判断出存在冲突或潜在冲突的航空器对.

3.3 与传统方法的比较分析

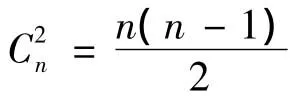
在实际运行中，空域内航空器的空间位置会随着时间推移而发生变化，因此为了实现对航空器进行全程飞行冲突探测，需将飞行全程所需的时间划分为若干个时间段，在每个时间段内实时更新航空器的三维空间坐标，直至该航空器飞出此空域.在此动态情况下，利用全空间计算方法和三维Delaunay剖分方法需在每个时间段均对全部航空器进行重新计算，效率较低且可延续性较差，而本文方法只需局部更新距离矩阵中的部分信息即可完成冲突的重新探测.

此外，若空域内的航空器数量规模较大，利用全空间计算方法和三维Delaunay剖分方法的计算复杂度较高，而且其中有相当规模的计算对冲突探测结果是没有影响的(如距离较远的航空器对之间的距离)，本文通过自适应地计算K值可以尽量避免对结果“无影响”的距离计算，从而提高了计算效率和稳定性.

4 算例

利用Matlab软件实现本文方法，并对自由飞行条件下的冲突探测进行模拟仿真实验.假设空域范围为100 km×100 km，随机生成25架航空器的空间位置、航向和速度等信息.本文判定两架航空器是否存在冲突或潜在冲突的规则是:当它们的水平距离小于最低水平间隔标准10 km，且垂直距离小于最低垂直间隔标准0.3 km时，意味着它们已经发生冲突;当水平间隔大于10 km而小于15 km时，表示两架航空器存在潜在冲突.

4.1 冲突及潜在冲突探测结果

首先假设某时刻空域内有25架在不同高度层飞行的航空器.在确定其空间位置坐标后，计算每架航空器的K-近邻(取K=5)，结果如表1所示.其中，每个单元格括号中的第一个数字代表航空器序号，第二个数字代表它们之间的距离.例如，第1行第1列的单元格中(22，12.3)表示A1航空器与A22航空器之间的距离为12.3 km.对于每架航空器，其K-近邻是按照距离由小到大排列的，以方便飞行冲突的探测.

利用前面提到的冲突判定规则对表1进行搜索，可以得到存在冲突以及潜在冲突的航空器对，具体结果为:

存在冲突的航空器对包括(A6，A12，7.8)，(A9，A10，8.1);

存在潜在冲突的航空器对包括(A1，A22，12.3)，(A3，A23，13.1)，(A11，A13，14.6).

图2所示为从不同角度展示的冲突探测结果，其中实线段表示存在冲突的航空器对，虚线段表示存在潜在冲突的航空器对.

表1 航空器的K-近邻计算结果Table 1 KNN calculation result of aircraft

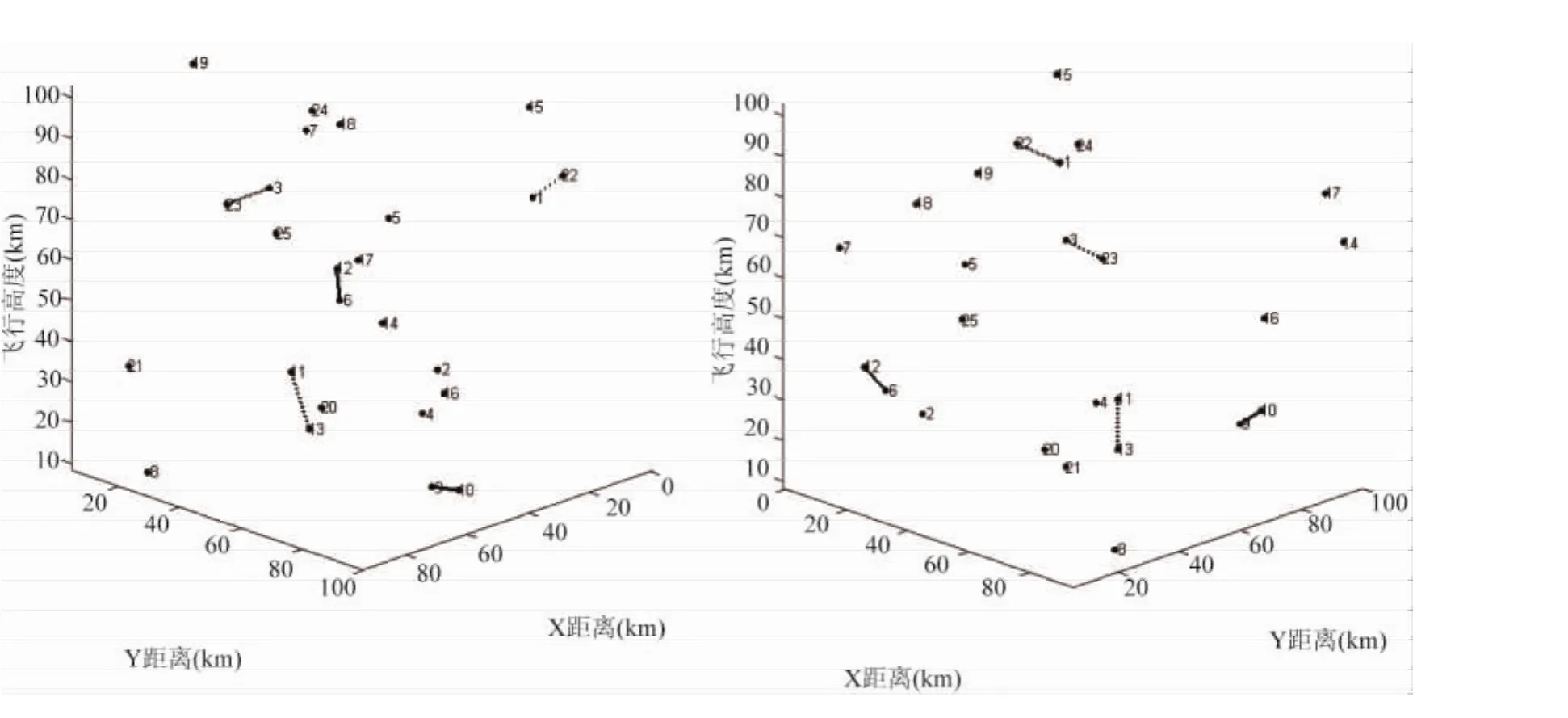
图2 航空器冲突探测结果Fig.2 Conflict detection result of aircraft

当有另外一架航空器飞出(或飞入)此空域时，只需在表1中删除(或增加)一行，并修改表1中的部分距离信息，即可快速、准确探测是否由此航空器带来冲突风险.例如，在上述算例中，假设A1航空器飞出此空域，只需删除表1中的第1行数据，清空第15行第1列以及第22行第1列的单元格，并将每行剩余的距离数据向前递补即可进行重新探测.

4.2 本文方法与传统方法的对比

针对上述算例，在实验环境为2.4 GHz CPU，4 GB内存的PC机上，分别采用全空间计算方法和三维Delaunay剖分方法进行冲突探测计算，均可得到与表1相同的计算结果.然而，三种方法的计算复杂度和速度却有较大的区别.表2所列为每种方法的计算复杂度，以及针对不同规模的航空器进行冲突探测所需的距离判断次数和计算时间.相比于两种传统的计算方法，本文方法在计算复杂度和计算速度方面均有显著的优势.而且航空器的数量规模越大，本文方法在计算效率方面的优势就越明显.

表2 实验数据统计Table 2 Experimental data statistics

对上述25架航空器进行冲突探测时，所需距离判断次数的示意图如图3所示.若两架航空器需要将它们之间的距离与冲突判定规则进行比较，则将它们用一条线段相连.由图3可以直观地看出本文方法与传统方法相比大幅度地减少了距离判断次数，从而节省了计算时间，提高了计算效率.

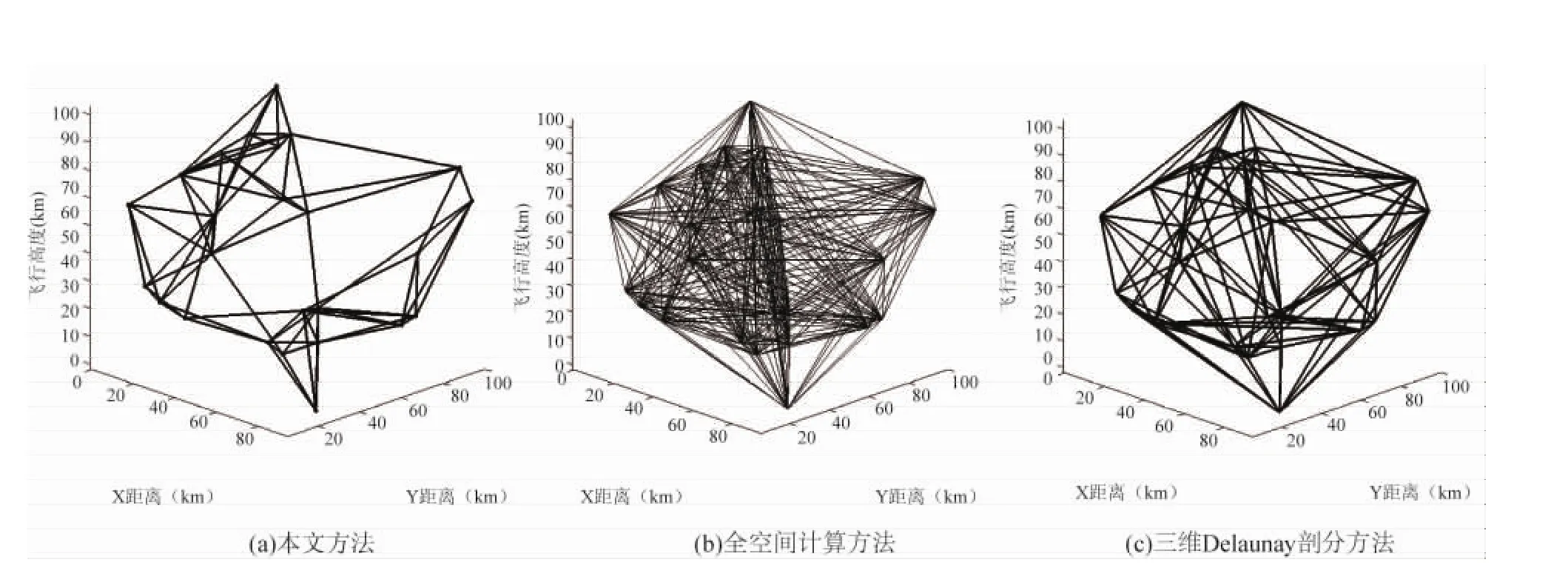
图3 与传统方法对比结果Fig.3 Comparison result with traditional methods

4.3 K值的自适应计算

如前文所述，本文方法在进行冲突探测时需要进行Kn次距离判断，因此K值的选取将直接影响计算复杂度.为了尽量减少计算时间，本文采用自适应的方法计算K值.首先，根据空域内航空器的数量将K赋值为一个较小的数值，然后利用K-近邻方法进行冲突探测.若某航空器与其第K个近邻存在冲突或潜在冲突，意味着与其存在冲突的航空器可能不止K个，因此将K值增大ΔK至K'，再通过计算该航空器的K'－近邻进行冲突探测，直至其与第K'个近邻不存在冲突为止.一般来说，利用K的初始赋值即可探测出全部的冲突;即使出现上述情况，本文方法也只需对距离矩阵进行局部调整，最大限度地节省了计算时间.例如，假设空域内有120架航空器，利用本文方法求得距离矩阵，其中A39航空器、A92航空器均与其第K(K=5)个近邻存在潜在冲突，如表3所示.将K自适应增大至K'(K'=6)，重新计算这两架航空器的K'－近邻，发现其与第K'个近邻不存在潜在冲突，则计算结束，如表4所示.

表3 K-近邻对应的距离矩阵Table 3 Distance matrix for KNN

表4 K'－近邻对应的距离矩阵Table 4 Distance matrix for K'NN

从上述仿真结果可以看出，本文所采用的K-近邻方法避免全局搜索，只在每架航空器周围进行局部搜索就能有效地探测出在自由飞行条件下的航空器群之间的飞行冲突.在不同时间段内，当航空器的位置发生变化时，只需局部修改距离矩阵，即可实时、准确地探测飞行冲突，大幅度节省了计算时间，为管制员进行冲突解脱创造条件.

5 研究结论

(1)本文采用K-近邻方法对在三维空间中自由飞行的航空器进行冲突探测，通过理论分析与仿真实验，表明本文方法能够快速、有效地探测出存在冲突或潜在冲突的航空器.此外，当航空器位置发生变化时，只需局部修改距离矩阵即可重新探测，大幅度提高了计算效率.

(2)对于K值的确定，本文提出了其自适应计算方法，当K的初始赋值不能探测到全部的冲突时，通过适当增加K值、局部调整距离矩阵即可解决该问题.

(3)本文方法只能对航空器进行冲突探测，而无法给出具体的解脱策略，这也是本文的未来发展方向.

［1］Final report of RTCA task force 3-free flight implementation［R］.Washington DC:RTCA Inc，1995.

［2］周向华.冲突探测与解脱技术在未来空中交通管理中的应用［D］.南京:南京航空航天大学.2009.［ZHOU X H.Research on technologies of the conflict detection and resolution for future air traffic management［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2009.］

［3］Alliot J M，Gruber H，Joly G，et，et al.Geneticalgorithms for solving air traffic control conflicts［C］//The Ninth Conference on Artificial Intelligence for Applications，1993:338-344.

［4］Krozel J，Mueller T，Hunter G.Free flight conflict detection and resolution analysis［C］//AIAA Guidance，Navigation and Control Conference，San Diego，California USA，July，1996.

［5］Versteegt H H，Visser H G.Traffic complexity based conflictresolution［J］.Air Traffic Control Quarterly，2003，11(2):103-122.

［6］靳学梅，自由飞行行空域中多机冲突探测与解脱技术研究［D］.南京:南京航空航天大学.2004.［JIN X M.The research of technologies on the conflict detection and resolution among multi-aircraft in free flight airspace［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2004.］

［7］程丽媛.自由飞行空域中多机冲突探测与解脱技术研究［D］.南京:南京航空航天大学.2005.［CHENG L Y.Research on technologies of the conflict detection and resolution among multi-aircraft in free flight airspace［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2005.］

［8］刘星，胡明华，韩松臣.自由飞条件下的冲突探测与解脱方法［J］.南京理工大学学报，2002，26(增刊):56-60.［LIU X，HU M H，HAN S C.The study on flight conflicts detection and solving［J］.Journal of Nanjing University of Science and Technology，2002，26(Supp):56-60.］

［9］刘星，韩松臣.用于自由飞行冲突探测的Delaunay方法［J］.数据采集与处理，2002，17(4):446-449.［LIU X，HAN S C.Delaunay method for free flightconflict detection［J］. Journal of Data Acquisition ＆ Processing，2002，17(4):446-449.］

［10］刘昕.基于计算几何方法的飞行冲突检测［J］.电子测量技术，2007，30(4):87-89.［LIU X.Conflict detection in free flight based on computational geometry method［J］. Electronic Measurement Technology，2007，30(4):87-89.］

［11］T M Cover，P E Hart.Nearest neighbor pattern classification［J］.IEEE Transactions on Information Theory，1967，13(1):21-27.

［12］刘晓红.基于支持向量机和K近邻的联合分类研究［D］.哈尔滨:哈尔滨工程大学.2011.［LIU X H.Research on the joint classification based on support vector machine and K-nearest neighbor［D］.Harbin:Harbin Engineering University，2011.］

［13］周而重，逄玉俊.一种改进的K近邻法在模式识别中的应用［J］.沈阳师范大学学报(自然科学版)，2007，25(4):475-478.［ZHOU E Z，PANG Y J.Application of an improved K-nearest neighbor approach in pattern recognition［J］. Journalof Shenyang NormalUniversity(NaturalScience)，2007，25(4):475-478.］

［14］V Vaidehi，S Vasuhi，R Kayalvizhi，et al.Person authentication using face recognition［C］//Proceedings of the World Congress on Engineering and Computer Science，2008.

［15］徐晓艳.基于K近邻算法的中文文本分类研究［D］.合肥:安徽大学.2012.［XU X Y.Research of Chinese text classification based on K neighbor algorithm［D］.Hefei:Anhui University，2012.］

［16］鲁婷.K-近邻中文文本分类方法的研究［D］.合肥:合肥工业大学.2010.［LU T.The research on K-nearest neighbor Chinese text categorization algorithm［D］. Hefei:HeFei University of Technology，2012.］

［17］于滨，邬珊华，王明华，等.K近邻短时交通流预测模型［J］.交通运输工程学报，2012，12(2):105-111.［YU B，WU S H，WANG M H，et al.K-nearest neighbor model of short-term traffic flow forecast［J］.Journal of Traffic and Transportation Engineering，2012，12(2):105-111.］

［18］杨小运.约束Delaunay三角剖分算法的研究与应用［D］.武汉:武汉科技大学.2012.［YANG X Y.The research and application of the delaunay triangulations algorithm［D］. Wuhan:Wuhan University of Science and Technology，2012.］