几何相位分析法(GPA)基本原理

郭红艳

辽宁广播电视大学锦州分校(锦州 121000)

分析固体物质微观结构中的应变场，对于丰富人们对微观世界的认识有着十分重要的意义。获得该应变场的方法有两种常用方法：peak-finding(PF)法和geometric phase images(GPA)法。相比而言，材利用高分辨像处理技术分析获得位移场和应变场大小的几何相位分析方法，其精度和应用范围较peak-finding方法更高和更广泛。其精度可达0.003nm[1]，并已用于半导体材料裂纹、位错和结构合金中小的析出相周围位移场和应变场的测量[2-4]。GPA方法是M.J.Hytch教授在1998年的Ultramicroscopy杂志上首先提出。由于HRTEM像可以由经过Fourier变换后某一带轴2维的Bragg反射谱所表征。周期排列的2维强衍射斑点中蕴含晶体结构信息。选择两个非线性相关的衍射斑点就可以定义正空间的2维高分辨像，并以此为参考可以度量实验高分辨像晶格的畸变。

GPA的基本原理：

完整晶体的HRTEM像的强度可以用公式(1)来描述：

其中： )(rI 表示在位置r处像的强度，g是与布拉格反射点相关的周期性。傅里叶互相关系数gH 可以用公式(2)描述：

其中gA表示振幅，gP表示相位。

为了说明像的强度随位置的变化而改变，将gH看做位置的函数：

相关系数 )(rHg可以解释为傅里叶分量gH 的实际值。为了将上述函数用傅里叶空间表达，必须对变换后的强度定义为：

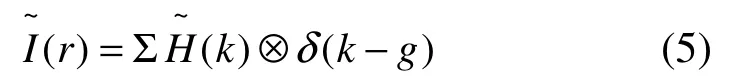
公式(3)的傅里叶变换为：用与倒易空间矢量g的卷积操作表示。对于完

算符表示卷积计算，因此公式(5)说明可以整晶体HRTEM像的傅里叶变换

位置时其值才不为零并且函数是高的δ函，只有其处于布拉格数。如果在图像某位置有变化，那么在傅里叶变换过程中布拉格衍射位置直接会变成非零。在一个布里渊区，g可以写成：

这可以引入掩模函数提取相应信息。

这样，公式(5)给出的HRTEM像强度的傅立叶变换可以用公式(9)表达出来。

完整晶体高分辨像傅里叶变换分量gH ，强度I( r)分别用来表征与衍射矢量g相对应的高分辨像的

接下来 )(rHg可以按照公式(9)进行定义振幅和相位。按照公式(2)的定义，将公式(1)写成振幅Ag和相位 Pg的形式，并用该公式用于真实图像上，考虑到傅里叶变换后图像存在共轭对称特性，因而可得公式(10)：

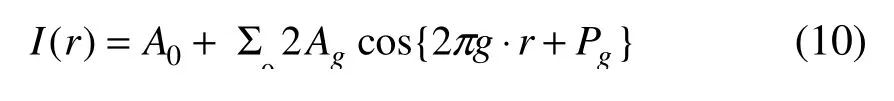
特定晶面的晶格条纹 )(rBg科研用公式(11)描述

将掩膜板放置于傅里叶变换后的±g衍射矢量位置，可以得到原图像的布拉格滤波像。在晶格条纹出现变化的时候，在傅里叶变换后的衍射图中仍保留共轭对称性：

利用公式(7)和(8)定义的布里渊掩膜板过滤得到的布拉格滤波像的强度可以表示为：

假设倒易空间晶格矢量相对于完整晶体倒易空间矢量发生了改变，既：

式中：gΔ表示在倒易空间中相对于完整晶体的改变量。这样公式(11)则可以写成

将公式(15)与公式(13)进行比较可知，相位作为位置的函数可以表示为：

忽略任意完整晶体产生的常数相位gP，那么由于倒易空间晶格矢量的变化在相位图上必定产生位移量的明显变化。

针对具体的HRTEM图像，GPA分析的过程是：首先对HRTEM像利用适当的掩膜板滤波后进行傅里叶变换得到含有强度信息的倒易空间的衍射谱；选择一个衍射斑点作参考的矢量g，利用适当的掩膜板做滤波处理；接着计算原始图像傅里叶变换后的强度于位置矢量g；进行反傅里叶变换可以计算出

按照公式(2)将 )(rHg写成振幅和相位形式：

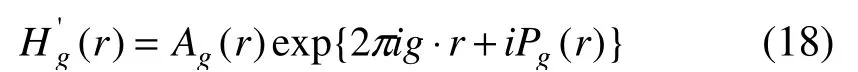
接着按下面公式计算布拉格滤波后的像强度

公式中eℜ表示实部，表示HRTEM像的原始相位，对微分可以得到可用于确定局部倒易空间矢量的改变量将原始相位减去常量)(2rgπ就可以得到)(rPg。

利用两个线性无关的倒易矢量1g和2g可以确定与之相对的相位 )(rPg。

用矩阵方式表示位移场：

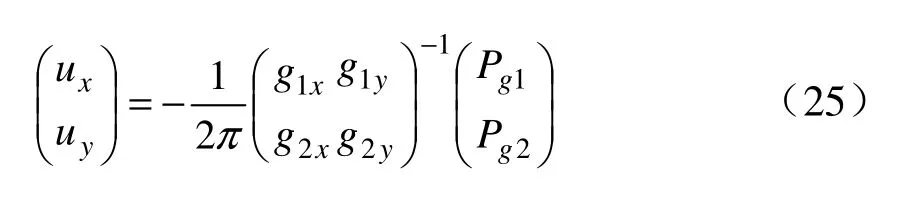
令按照线性代数原理可得T表示矩阵的转置，带入公式（25）可得：

根据弹塑性力学原理将公式（26）求导数，得到应变场大小：

[1]Hÿtch M J,Putaux J-L,Pénisson J-M.Measurement of the displacement field of dislocations to 0.03Å by electron microscopy[J].Nature,2003,423:270-273.

[2]Zhao C W,Xing Y M,Bai P C.Quantitative measurement of deformation field aroundlow-angle grain boundaries by electron microscopy[J].Physica B,2008,403(10-11):1838-1842.

[3]侯小虎,白朴存,赵春旺,邢永明.喷射沉积Al-Zn-Cu-Mg合金GP区应变场的定量测量[J].实验力学,2011,26(1):16-20.

[4]Zhao C W,Xing Y M,Bai P C.Experimental examination of displacement field in an edge dislocation core in aluminum[J].Physics Letters A,2008,372(3):312-315.

[5]Hÿtch M J,Snoeck E,Kilaas R.Quantitative measurement of displacement and strain fields from HREM micrographs[J].Ultramicroscopy,1998,74:131-146.