从DSC 曲线数据计算/确定含能材料自催化分解反应动力学参数和热爆炸临界温升速率的方法

胡荣祖 赵凤起 高红旭 姚二岗 张 海 王 尧常象宇 赵宏安

(1西安近代化学研究所燃烧与爆炸技术重点实验室,西安710065;2西北大学数学系数据分析和计算化学研究所,西安710069;3西安交通大学信息科学与系统科学研究所,西安710049;4西北大学信息科学与工程学院,西安710069)

1 引言

放热分解反应体系热爆炸的临界温升速率(dT/dt)Tb,是评价含能材料(EMs)安定性和安全性的重要参数.在表达这个参数方面,胡荣祖等从反应进度和能量变化的关系,1热分解过度到热爆炸的充分必要条件2和非等温反应的动力学方程3导出了绝热及近似绝热条件下,速率方程为dα/dt=A1exp(-Ea1/RT)(1-α)m+A2exp(-Ea2/RT)αn(1-α)p的表观经验级数和m=n=p=1的一级自催化分解反应体系(dT/dt)Tb值的估算式;3,4王耘等5导出了绝热和近似绝热条件下反应体系的dT/dt值的估算式,但对(dT/dt)Tb值的估算式未作研究.在估算这个参数方面,Hu等6-10估算了氮含量分别为11.92%、11.97%、13.54%、13.86%和14.14%的硝化棉(NC)的一级自催化分解反应体系的(dT/dt)Tb值;Eisenreich等11,12估算了NC一级自催化分解反应的动力学参数.在实测这个参数方面,胡荣祖等13研究了硝仿热爆炸的爆前加热、热分解温升和时间的关系.本工作作为文献3-12的拓展,报道了自催化反应速率方程分别为:dα/dt=Aexp(-E/RT)α(1-α),dα/dt=Aexp(-E/RT)(1-α)n(1+Kcatα),dα/dt=Aexp(-E/RT)[αa-(1-α)n],dα/dt=A1exp(-Ea1/RT)(1-α)+A2exp(-Ea2/RT)α(1-α),dα/dt=A1exp(-Ea1/RT)(1-α)m+A2exp(-Ea2/RT)αn(1-α)p,dα/dt=Aexp(-E/RT)·(1-α),dα/dt=Aexp(-E/RT)(1-α)n,dα/dt=A1exp(-Ea1/RT)+A2exp(-Ea2/RT)(1-α)和 dα/dt=A1exp(-Ea1/RT)+A2exp(-Ea2/RT)α(1-α)的(dT/dt)Tb估算式的导出途径和NC(13.54%N)自催化分解反应动力学参数和自催化分解转向热爆炸时(dT/dt)Tb值的估算结果.

2 理论和方法

单位时间内由于EMs热分解而放出的热量q1为

式中,Q为热分解反应的焓(J·mol-1),V为EMs的装填体积(cm3),d为装填密度(g·cm-3),M为EMs的摩尔质量(g·mol-1),dα/dt为机理函数为f(α)=α(1-α)的自催化反应(Au)速率:

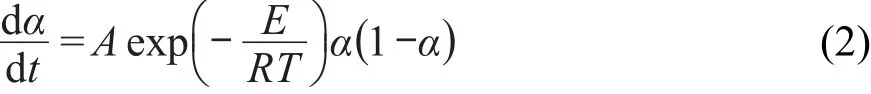
联立方程(1)和(2),得

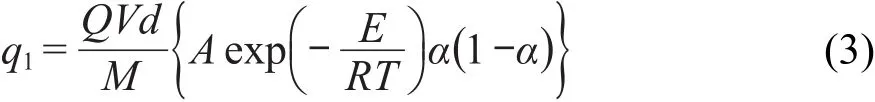
与此同时,单位时间内因传热由反应区通过器壁向四周环境散失的热量q2为

式中,k′为传热系数(J·cm-2·K-1·s-1),S表示药柱表面积(cm2);Tc为按照线性关系Tc=T0+βt确定的反应器壁和空间温度;β表示线性加热速率(K·min-1),T0表示热分析曲线离开基线的温度(K).

热爆炸发生时,方程(3)变为

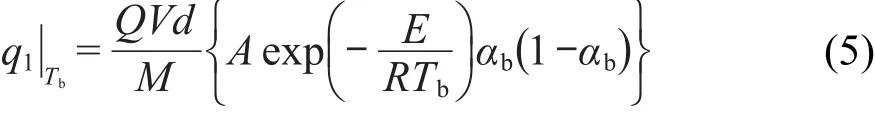
此处,αb是相应于Tb的α值,Tb是EMs的热爆炸温度(K).

方程(4)变为此处,Te0是β→0时的onset温度.

根据Semenov的热爆炸理论,2热分解过渡到热爆炸的充分必要条件式为

此处(dT/dt)Tb是热分解转向热爆炸时EMs中的临界温升速率.

方程(4)对T微分,得

方程(14)称为Au自催化分解反应转向热爆炸时的临界温升速率表达式.

一旦从热流曲线解得E、A、Te0、Tb和αb,就可从方程(14)得到(dT/dt)Tb的值.

类似地,由机理函数为 f(α)=(1-α)n(1+Kcatα))速率方程

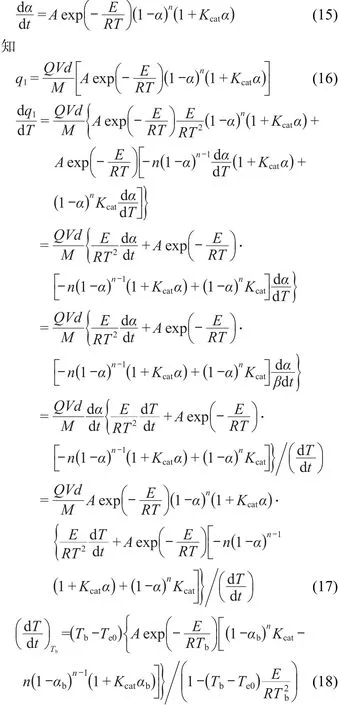
方程(18)称为CnB自催化分解反应转向热爆炸时的临界温升速率表达式.

一旦从热流曲线解得E,A,n,Kcat,Te0,Tb和αb,就可从方程(18)得(dT/dt)Tb值.

由机理函数为 f(α)=αa-(1-α)n的自催化反应(Bna)的速率方程方程(22)为Bna自催化分解反应转向热爆炸时的临界温升速率表达式.

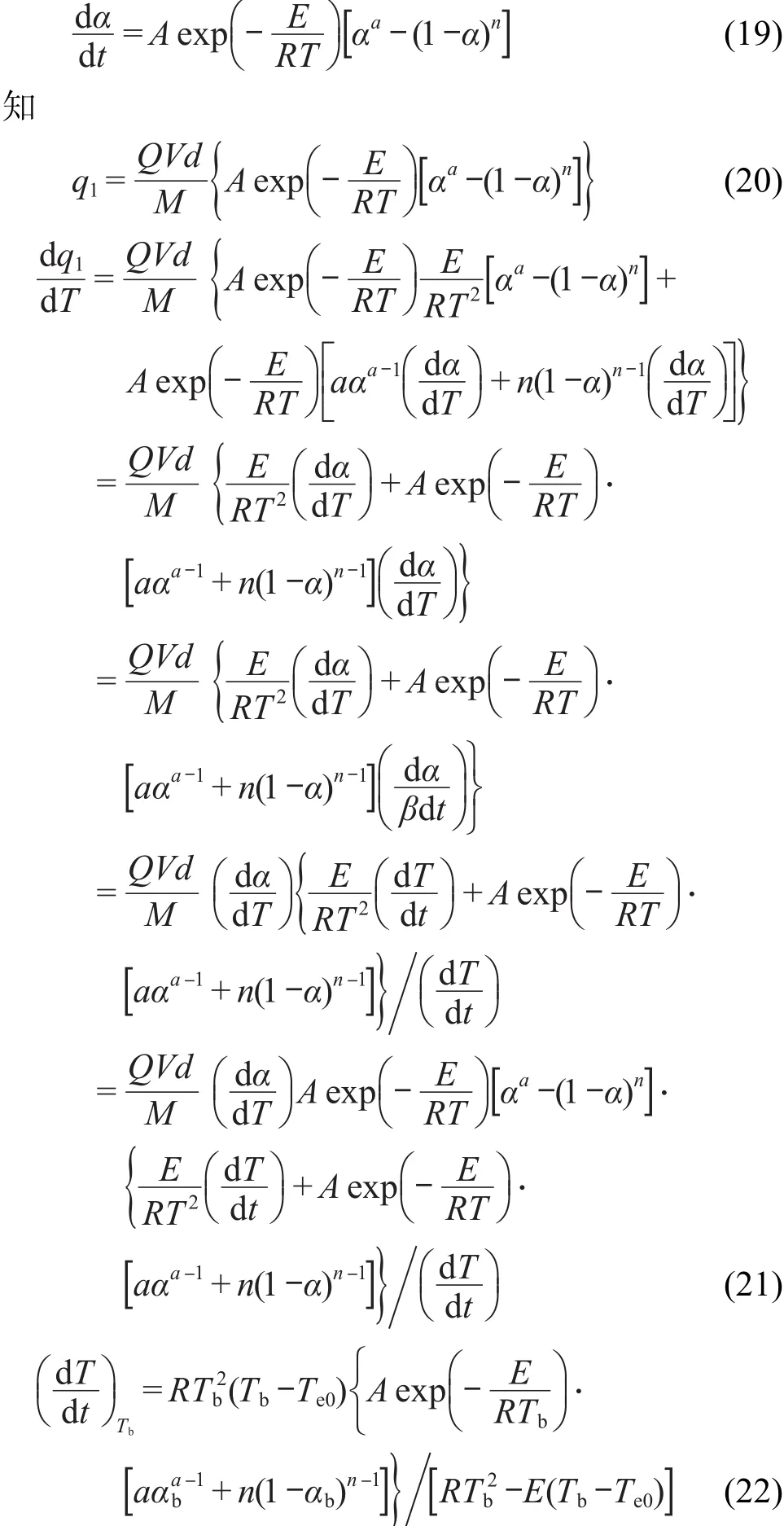
一旦从热流曲线解得E,A,Te0,n,a,Tb和αb,就可从方程(22)得(dT/dt)Tb值.

由一级自催化分解反应速率方程

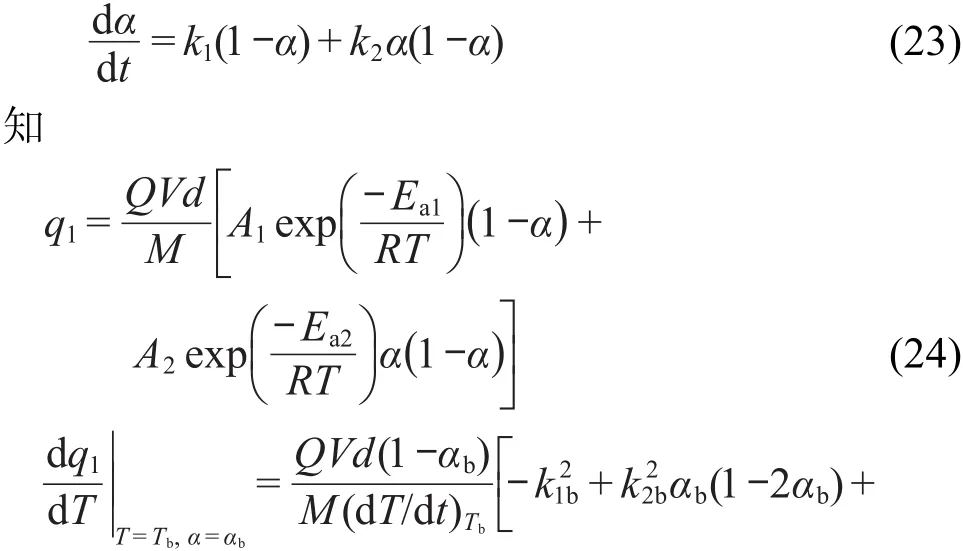
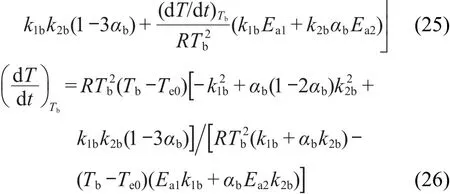
式中,k1=A1exp(-Ea1/RT),k2=A2exp(-Ea2/RT).

方程(26)称为一级自催化分解反应转向热爆炸时的临界温升速率表达式.

一旦从热流曲线解得Ea1,Ea2,A1,A2,Te0,Tb和αb,就可从方程(26)得(dT/dt)Tb值.

由经验级数自催化分解反应速率方程

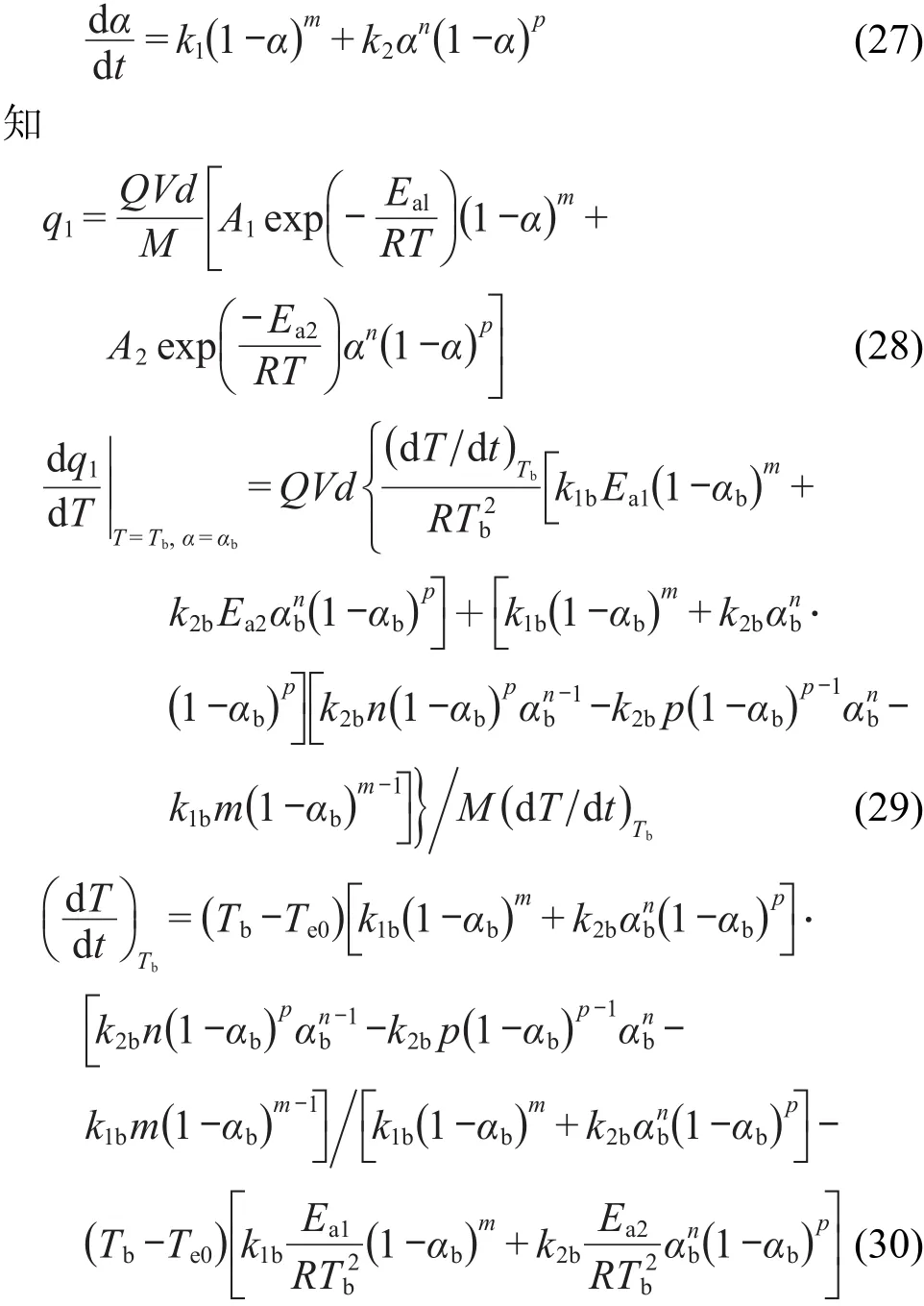
方程(30)称为表观经验级数自催化分解反应转向热爆炸时的临界温升速率表达式.

一旦从热流曲线解得Ea1,Ea2,A1,A2,Te0,Tb,αb,m,n和p,就可从方程(30)得(dT/dt)Tb值.

由简单一级自催化分解反应速率方程

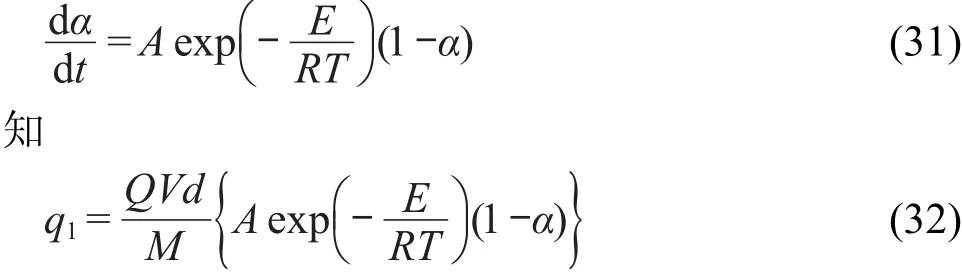
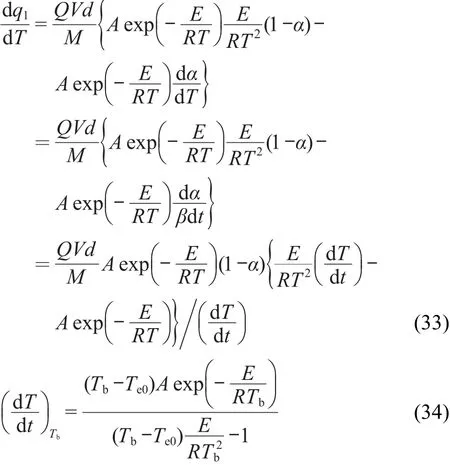
方程(34)为简单一级自催化分解反应转向热爆炸时的临界温升速率表达式.

一旦从热流曲线解得E、A、Te0和Tb,就可从方程(34)得(dT/dt)Tb值.

由简单n级自催化分解反应速率方程

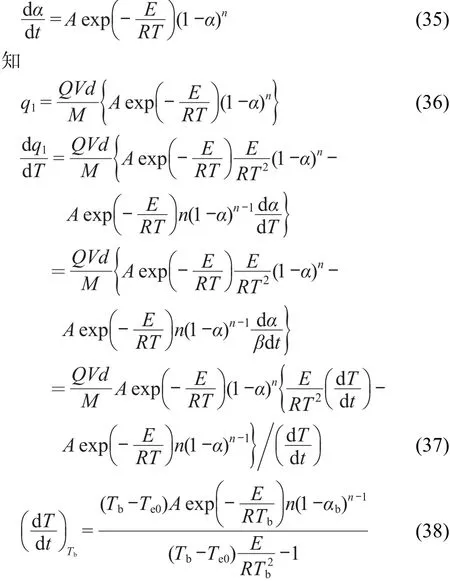
方程(38)称为简单n级自催化分解反应转向热爆炸时的临界温升速率表达式.

一旦从热流曲线解得E,A,Te0,n,Tb和αb,就可从方程(38)得(dT/dt)Tb值.

由经验级数m=0,n=0,p=1的自催化分解反应速率方程

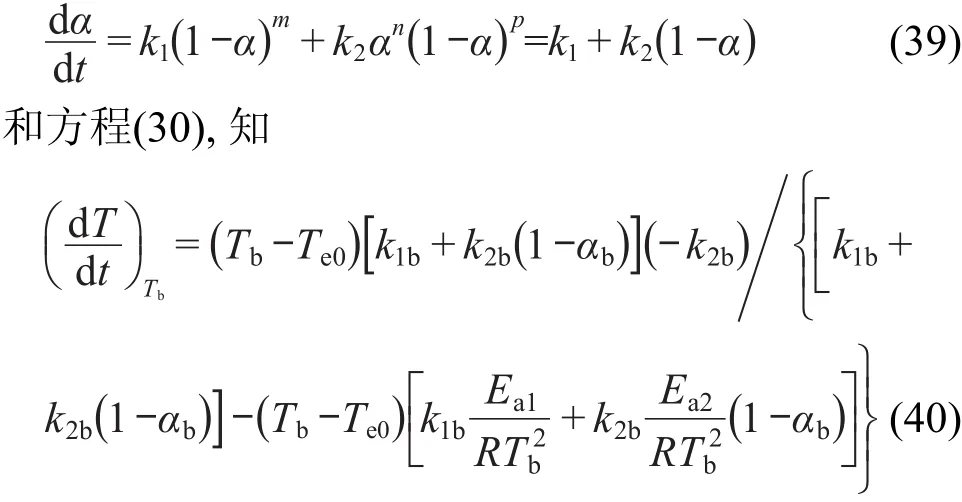
方程(40)称表观经验级数m=0,n=0,p=1的自催化分解反应转向热爆炸时的临界温升速率表达式.

一旦从热流曲线解得Ea1,Ea2,A1,A2,Te0,Tb和αb,就可从方程(40)得(dT/dt)Tb值.

由经验级数m=0,n=1,p=1的自催化分解反应速率方程

方程(42)称为表观经验级数m=0,n=1,p=1的自催化分解反应转向热爆炸时的临界温升速率表达式.

一旦从热流曲线解得Ea1,Ea2,A1,A2,Te0,Tb和αb,就可从方程(42)得(dT/dt)Tb值.

为求方程(2)和(31)中的2参数(A,E),方程(35)中的3参数(A,E,n),方程(15)、(19)、(23)、(39)和(41)中的4参数(分别为A,E,n,Kcat;A,E,a,n;A1,A2,Ea1,Ea2;A1,A2,Ea1,Ea2;A1,A2,Ea1,Ea2)和方程(27)中的7参数(A1,A2,Ea1,Ea2,m,n,p),进行了线性最小二乘法和信赖域方法14的数值模拟.

对n=1的自催化反应速率方程,有

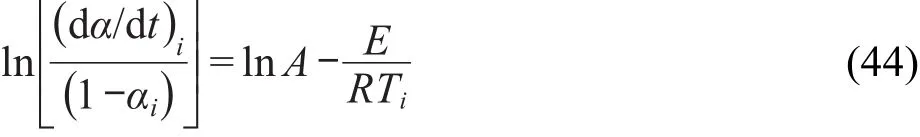
由方程(43)和(44)的左端项与1/T作图,用最小二乘法从斜率得E,截距得A.

经非线性优化模型:

对n级自催化反应速率方程,有

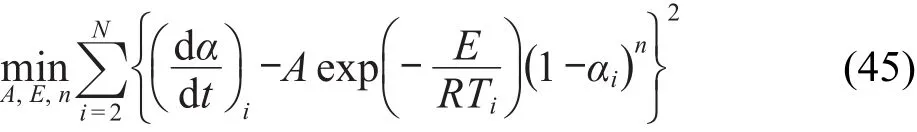
对CnB速率方程,有

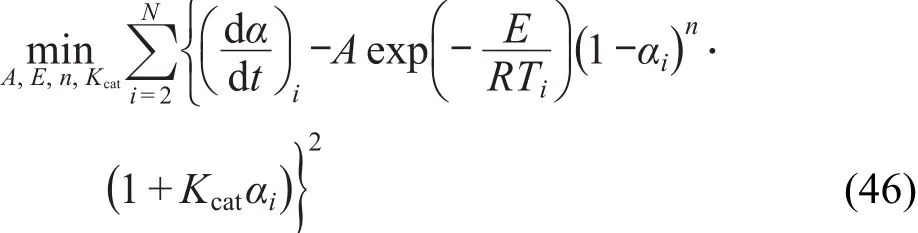
对Bna速率方程,有

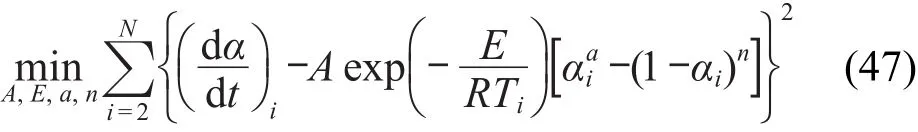
对一级自催化分解反应速率方程,有

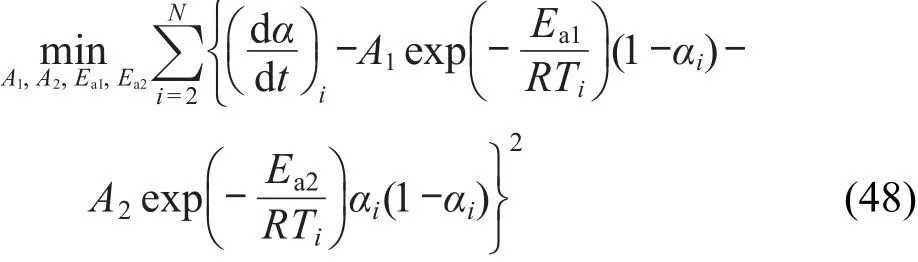
对经验级数自催化分解反应速率方程,有

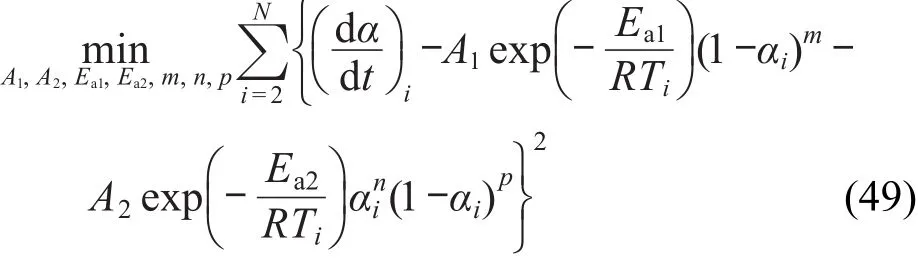
对经验级数m=0,n=0,p=1的自催化分解反应速率方程,有

对经验级数m=0,n=1,p=1的自催化分解反应速率方程,有

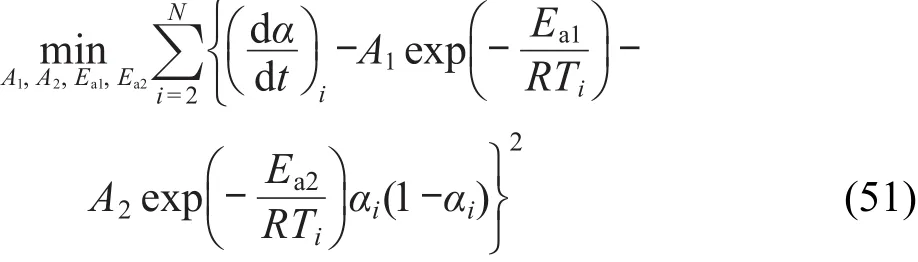
由最小化均方误差估计方程(45)中的3参数(A,E,n),方程(46)、(47)、(48)、(50)和(51)中的 4 参数(A,E,n,Kcat;A,E,a,n;A1,A2,Ea1,Ea2;A1,A2,Ea1,Ea2;A1,A2,Ea1,Ea2)和方程(49)中的7参数(A1,A2,Ea1,Ea2,m,n,p).

为准确估算NC(13.54%N)放热分解反应的动力学参数,进行了边界约束,限制参数范围,将方程(45)-(51)分别改写如下:

对n级自催化反应速率方程,有

对CnB速率方程,有

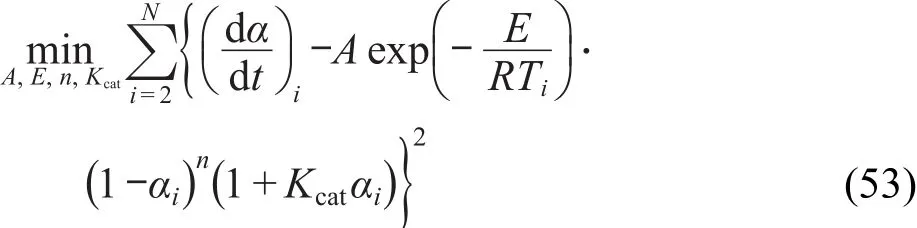
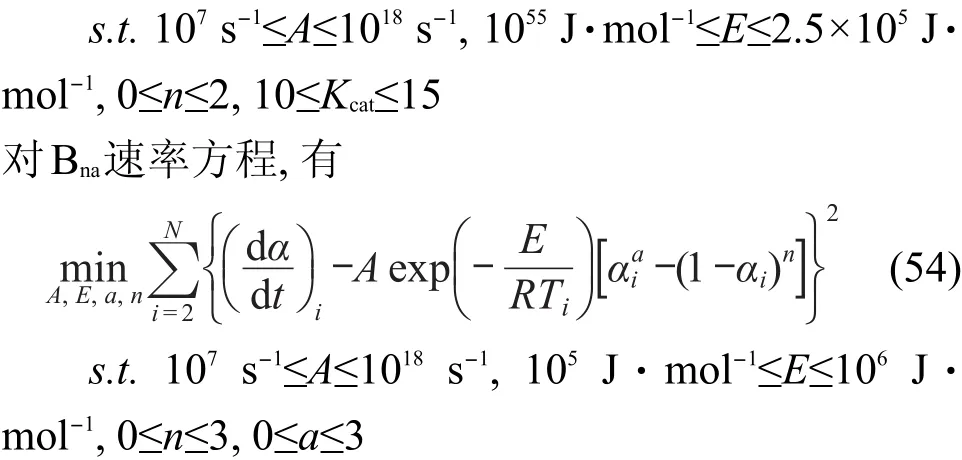
对一级自催化分解反应速率方程,有

对经验级数自催化分解反应速率方程,有

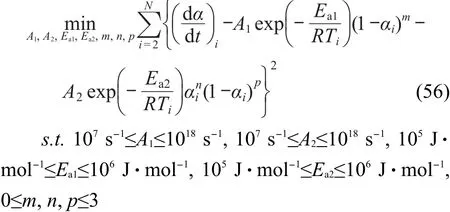
对经验级数m=0,n=0,p=1的自催化分解反应速率方程,有

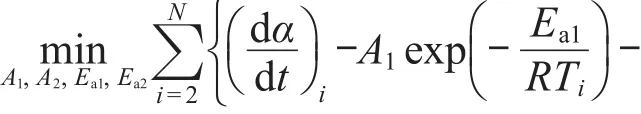
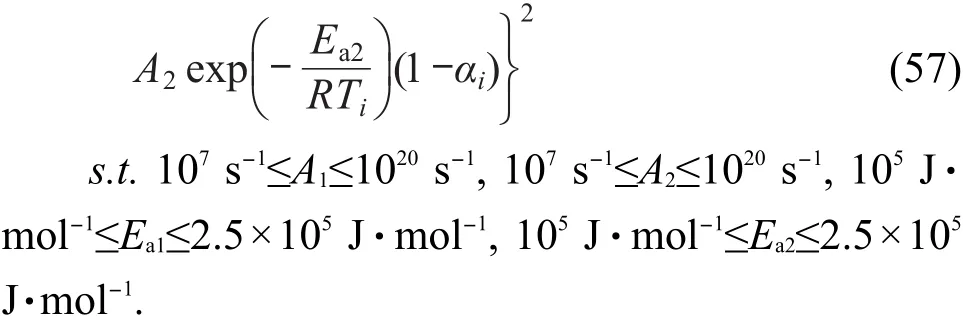
对经验级数m=0,n=1,p=1的自催化分解反应速率方程,有

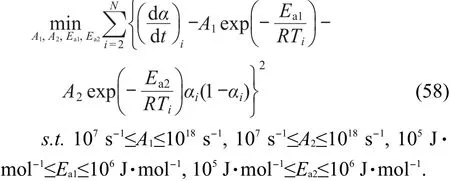
为叙述简便,将具有边界约束的非线性优化问题重新描述为

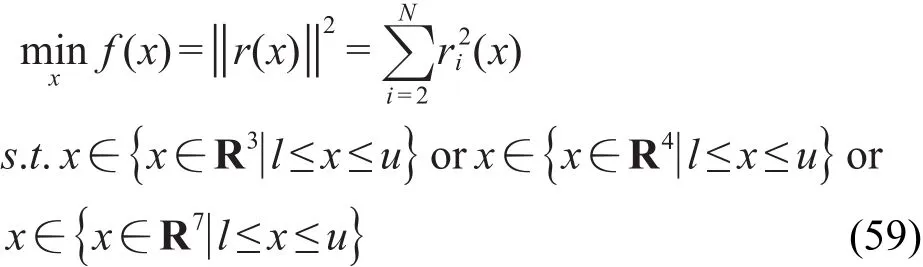
其中,对n级自催化反应速率方程,有

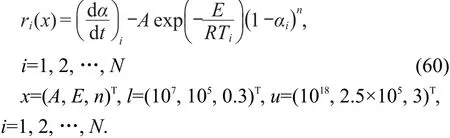
对CnB速率方程,有

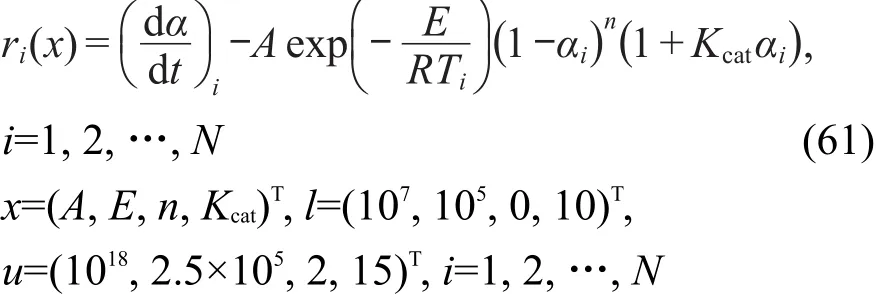
对Bna速率方程,有

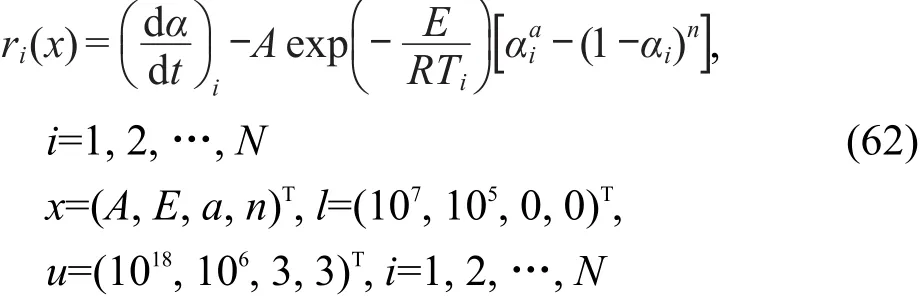
对一级自催化分解反应速率,有

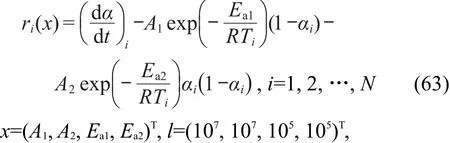
u=(1018,1018,106,106)T,i=1,2,…,N

对经验级数自催化分解反应速率方程,有

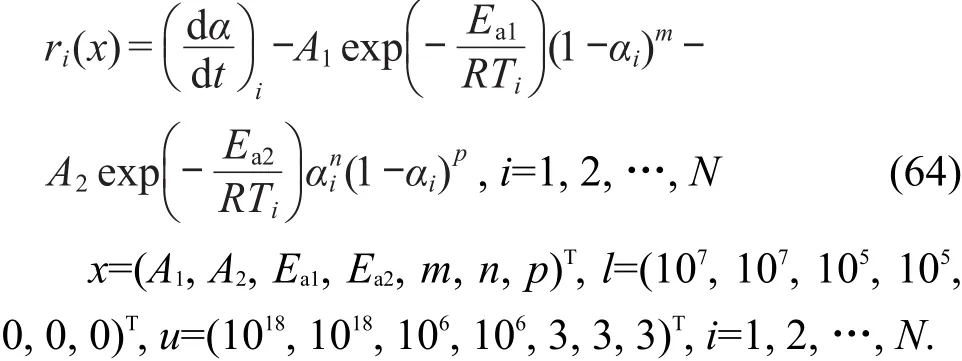
对经验级数m=0,n=0,p=1的自催化分解反应速率方程,有

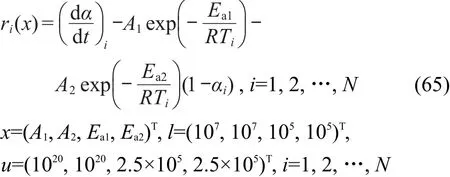
对经验级数m=0,n=1,p=1的自催化分解反应速率方程,有

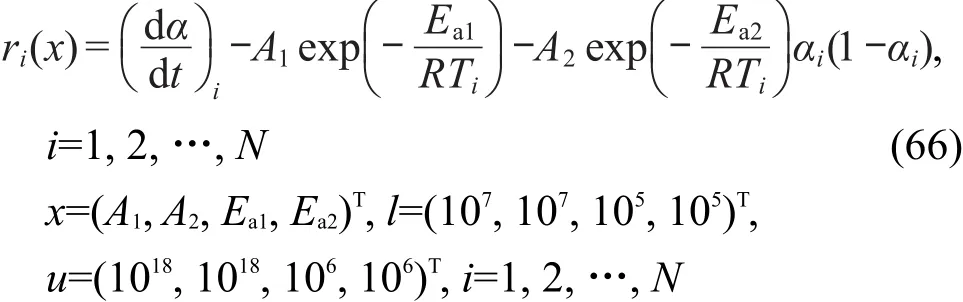
定义矩阵D(x)为D(x)≜ diag[|vi(x)|-1/2],即,D-2是一对角矩阵且其第i个对角元素为|vi(x)|.考虑非线性方程组

设xk∈int(Φ),式(59)的牛顿迭代满足

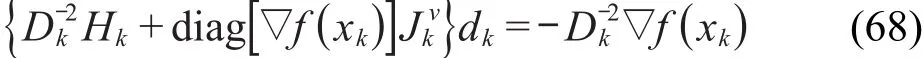
其中,M(x)≜B(x)+C(x),C(x)≜D(x)diag[g(x)]Jv(x)D(x),

业已证明,xk是式(59)的局部最小值点,当且仅当sk是下式的解

这里Δk为正数,表示信赖域的大小.因此,通过求解子问题(70)来确定xk是否为目标函数的最小值点是合理的,进而,当信赖域大小Δk足够大时,局部最小值的邻域中式(67)的牛顿迭代正好是信赖域子问题(70)的解.

解决具有边界约束的非线性优化问题的信赖域方法模型为:

取x0∈int(Φ),循环k=0,1,…

(1)计算f(xk),gk,Hk及Ck;

(2)根据式(70)计算sk且满足xk+sk∈int(Φ).

(3)计算

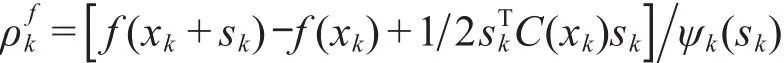
(5)修正模型yk,矩阵Dk及信赖域大小Δk.

信赖域大小Δk的修正为:给定0＜μ＜η＜1,γ1＜1＜γ2及Λl＞0,

3 计算实例

依据表1和表2中NC(13.54%N)放热分解反应的T-转化率(α)和β-Te关系数据,用方程(14),(18),(22),(26),(30),(34),(38),(40)和(42)分析表1和表2中数据,得表3中Au,CnB,Bna,一级/表观经验级数、简单一级和n级及表观经验级数m=0,n=0,p=1和m=0,n=1,p=1的自催化分解反应动力学参数和自催化分解反应转向热爆炸时的临界温升速率(dT/dt)Tb值.据此,发现9个微分方程中Au速率方程[方程(2)]算得的E和A值在EMs分解反应动力学参数正常范围[E=80-250 kJ·mol-1,lg(A/s-1)=7-30]17外,简单一级自催化分解反应方程[方程(31)]求E和A的线性相关系数为0.9157,远离0.98,所得(dT/dt)Tb为负值,属不合理,被排除.同时满足E和A值在正常范围内,(dT/dt)Tb为正值的方程有7个,在这7个方程中,以计算值与实验值的相对误差为判据,宜做描述NC(13.54%N)自催化分解反应过程的方程依次为:方程(27)、(23)、(41)、(39)、(19)、(35)、(15),对应误差依 次 为:0.0206、0.0255、0.0299、0.109、0.1698、0.1932、0.7620,相应热爆炸临界温升速率依次为:0.103、0.169、0.189、0.00002、0.615、0.020、0.266 K·s-1.由此认为,用相对误差最小的经验级数自催化反应速率方程描述NC(13.54%N)热分解过程是可取的,热分解转向热爆炸时的临界温升速率为0.103 K·s-1是可接受的.

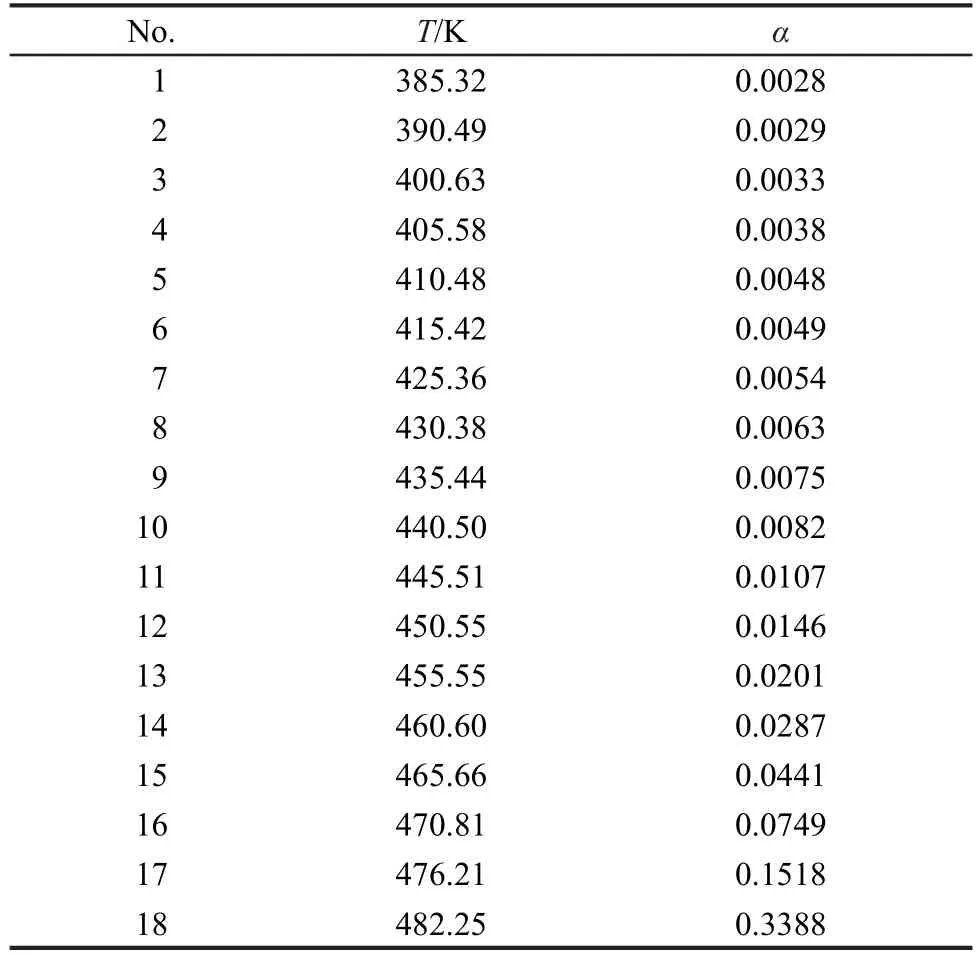
表1 用DSC测得的NC(13.54%N)的热分解数据8Table 1 Thermal decomposition data8of NC(13.54%N)determined by DSC

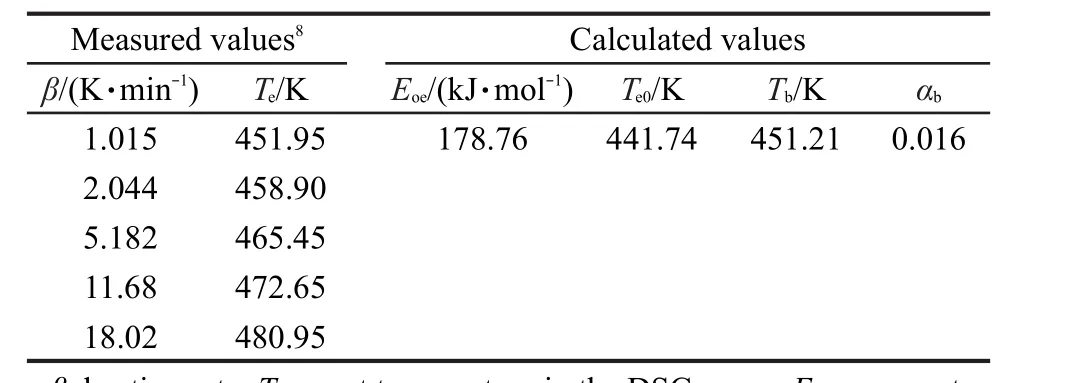
表2 NC(13.54%N)热爆炸临界温度(Tb)的计算值Table 2 Calculated values of the critical temperature(Tb)of thermal explosion for NC(13.54%N)

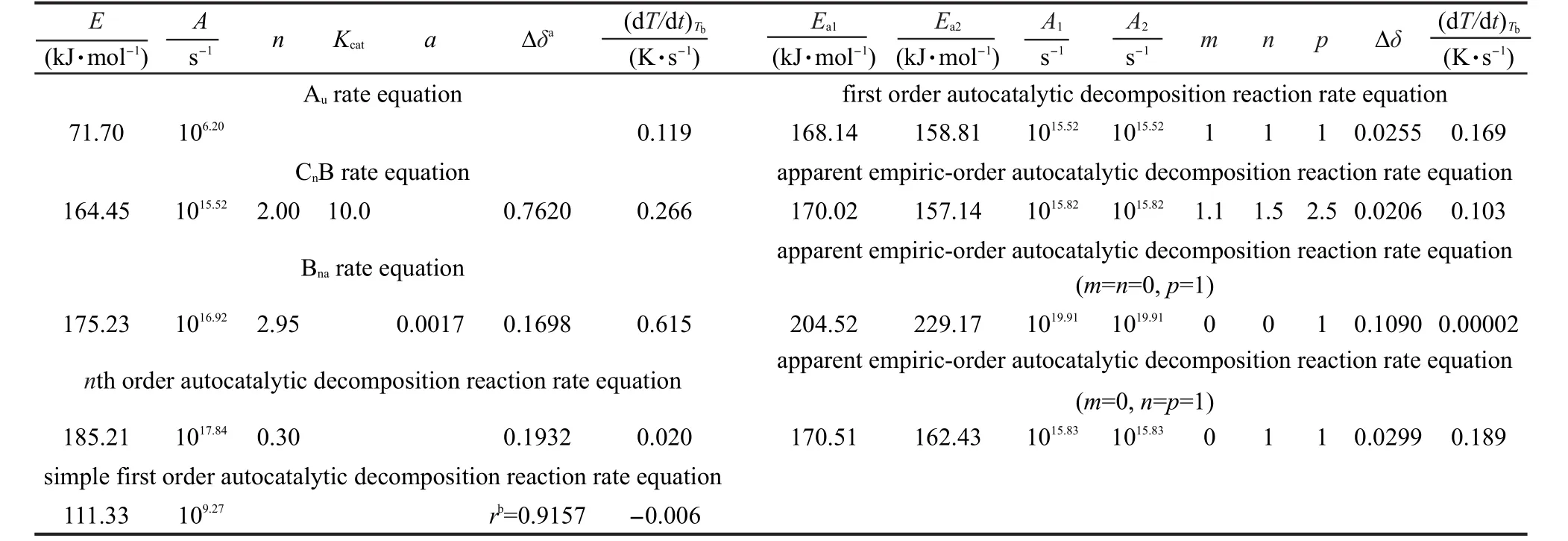
表3 用方程(14),(18),(22),(26),(30),(34),(38),(40)和(42)分析表1和表2中数据的结果Table 3 Results for analyzing the data in Tables 1 and 2 by Eqs.(14),(18),(22),(26),(30),34),(38),(40),and(42)

4 结论

(1)提出了从不同升温速率条件下的DSC曲线数据计算/确定EMs自催化反应的动力学参数和自催化分解转向热爆炸时的临界温升速率(dT/dt)Tb的方法.

(2)非等温条件下NC(13.54%N)热分解过程可用表观经验级数自催化分解反应动力学方程描述:

(3)NC(13.54%N)自催化分解反应过渡到热爆炸时的临界温升速率值为0.103 K·s-1.

(1) Deng,Y.Chem.J.Chin.Univ.1985,6(7),621.[邓 郁.高等学校化学学报,1985,6(7),621.]

(2) Semenov,N.N.On Some Problem of Kineties and Reactivity;Ind.,AN SSSR:Moscow,1958;p 421.

(3) Hu,R.Z.;Gao,S.L.;Zhao,F.Q.;Shi,Q.Z.;Zhang,T.L.;Zhang,J.J.Thermal Analysis Kinetics;Science Press:Beijing,2008;pp 322-334.[胡荣祖,高胜利,赵凤起,史启桢,张同来,张建军.热分析动力学.北京:科学出版社,2008:322-334.]

(4) Hu,R.Z.;Zhang,H.;Xia,Z.M.;Guo,P.J.;Gao,S.L.;Shi,Q.Z.;Lu,G.E.;Jiang,J.Y.Chin.J.Energ.Mater.2003,11(3),130.[胡荣祖,张 海,夏志明,郭鹏江,高胜利,史启桢,路桂娥,江劲勇.含能材料,2003,11(3),130.]

(5)Wang,Y.;Feng,C.G.;Zheng,X.Chin.J.Energ.Mater.2000,8(3),119.[王 耘,冯长根,郑 晓.含能材料,2000,8(3),119.]

(6) Hu,R.Z.;Guo,P.J.;Song,J.R.;Zhang,H.;Xia,Z.M.;Ning,B.K.;Fang,Y.;Shi,Q.Z.;Liu,R.;Luo,G.E.;Jiang,J.Y.Chin.J.Explo.Prop.2003,26(2),53.

(7) Ning,B.K.;Hu,R.Z.;Zhang,H.,Xia,Z.M.;Guo,P.J.;Liu,R.;Luo,G.E.;Jiang,J.Y.Thermochim.Acta 2004,416(1-2),47.doi:10.1016/j.tca.2003.11.029

(8)Hu,R.Z.;Guo,P.J.;Gao,S.L.;Zhang,H.;Xia,Z.M.;Ning,B.K.;Fang,Y.;Shi,Q.Z.;Liu,R.Chinese Journal of Polymer Science 2003,21(3),285.

(9) Guo,P.J.;Hu,R.Z.;Zhang,H.,Xia,Z.M.;Song,J.R.;Gao,S.L.;Ning,B.K;Liu,R.;Lu,G.E.;Jiang,J.Y.Chem.Res.Chin.Univ.2004,20(2),163.

(10)Zhang,H.;Xia,Z.M.;Guo,P.J.;Hu,R.Z.;Gao,S.L.;Ning,B.K.;Fang,Y.;Shi,Q.Z.;Liu,R.Journal of Hazardous Materials 2002,94(3),205.doi:10.1016/S0304-3894(02)00118-8

(11) Eisenreich,N.Beitrag Zur Kinetic Thermischer Zersetzungseaktionen(ThermoanalytischeAuswertung Der Zersetzung Von Nitrocellulose).Ph.D.Dissertation,Technical University of Munich,Munich,1978.

(12) Eisenreich,N.;Pfeil,A.Thermochim.Acta 1983,61(1-2),13.doi:10.1016/0040-6031(83)80300-1

(13) Hu,R.Z.;Song,Q.C.;Xie,J.J.;Liang,Y.J.Explosion and Shock Waves 1987,7(3),217.[胡荣祖,松全才,谢俊杰,梁燕军.爆炸与冲击,1987,7(3),217.]

(14)Thomas,F.C.;Li,Y.Y.SIAM Journal on Optimization 1996,6(2),418.doi:10.1137/0806023

(15) Ozawa,T.Bulletin of the Chemical Society of Japan 1965,38(1),1881.

(16) Zhang,T.L.;Hu,R.Z.;Xie,Y.;Li F.P.Thermochim.Acta 1994,244(3),171.

(17)Hu,R.Z.;Yang,Z.Q.;Ling,Y.J.Thermochim.Acta 1988,123,135.doi:10.1016/0040-6031(88)80017-0