非血红素铁(III)活化氧分子反应的自旋轨道耦合和零场分裂

吕玲玲 王小芳 朱元成 刘新文 袁 焜 王永成

(1天水师范学院生命科学与化学学院,甘肃天水741001;2西北师范大学化学化工学院,兰州730070)

1 Introduction

The mononuclear non-heme iron enzymes are an important group with a diverse range of chemical reactions including dioxygenation,hydroxylation,ring closure,oxidative desatura-tion,and aromatic ring cleavage.1Within this broad class,the oxygen-activating enzymes are one of the most extensively studied fields.1-4Most non-heme oxygenases catalyze O2activation using a high spin Fe(II)site through a redox process that also involves the substrate to provide the required number of electrons.By contrast,a small group of non-heme iron enzymes perform a high spin Fe(III)site to activate substrate for direct attack by O2,such as the lipoxygenases and intradiol dioxygenases.

Protocatechuate 3,4-dioxygenase(3,4-PCD)is one of the intradiol dioxygenase family.It catalyzes the ring cleavage of protocatechuate(PCA)to form β-carboxy-cis,cis-muconate,with the incorporation of both oxygen atoms from molecular oxygen.Based on different electronic descriptions of the enzyme-substrate(ES)complex,various mechanisms1have been proposed for the initial O2binding and activation steps,but they have not been definitively observed,therefore are not well understood.Mechanism forcatecholring cleavage by non-heme iron intradiol dioxygenases has been computationally investigated using density functional theory(DFT)by Borowski and Siegbahn.5In 2003,Deeth and Bugg6have also reported the studied results for the extradiol cleavage mechanism.But,in these investigations,the electronic structures and intersystem crossing processes of the initial O2binding complexes have not been discussed in detail.

However,we know that the chemistry of transition metals and their compounds(especially,metal-containing enzymes complexes such as cytochromes P450 and non-heme iron)is strongly influenced by the availability of multiple low-lying electronic states in these species.7-9Shaik and co-workers10have proposed that multiple spin states play an important role in these reactions,with many of them involving what they have called“two-state reactivity(TSR)”.The initial complexes of the triplet ground state O2(S=1)bound to Fe(III)(S=5/2)of 3,4-PCD-PCA can have a total spin of S=7/2,S=5/2,or S=3/2,and form the different spin state complexes.This means that the reactions should involve spin-conserving and spin-inversion processes.These will result in the complexity of the reaction mechanism.

Therefore,detailed analyses of electronic structures and intersystem crossing processes in the initial complexes are very important in order to better understand the O2activation mechanism.In present paper we computed electronic exchange coupling(J)and zero-field splitting(ZFS)using qausi-restricted theory at the DFT level11implemented with the program ORCA.12Then spin-orbit coupling(SOC)matrix elements were obtained by the approximate one-electron spin-orbit Hamiltonian.13Some very meaningful conclusions have been obtained by these calculations.

2 Computational details

2.1 Step of the system

The activate-site geometric structure of 3,4-PCD-PCA was obtained from the averaged crystallographic coordinate of P.putida 3,4-PCD complex with PCA(PDB code 3PCA).14Hydrogen atoms were placed at standard bond lengths and angles.Optimize calculations were performed on a model of the triplet state O2(S=1)bound to 3,4-PCD-PCA involving two Me-imidazoles to model His460 and His462,4-Me-phenolate to model Tyr408,and a bidentate PCA in the fully deprotonated state,which is shown in Scheme 1.

Unrestricted calculations allow α and β electrons to occupy orbitals with different spatial localizations and,can describe the spin localized on two different paramagnetic centers.Therefore,density functional theory calculations were performed using the Gaussian 03 program15with spin-unrestricted functional U-BP86 with 10%Hartree-Fock exchange and the Pople triple-ζ basis set,6-311G(d)to optimize geometry of the active model described above.For comparison,calculations were also performed with the spin-unrestricted U-B3LYP functional with the LanL2DZ effective core potential basis set.Transition state structures were found to have one imaginary frequency,which correlated to the motion of the bond being broken or formed.

2.2 Calculations of zero-field splitting(ZFS)tensor

In the absence of nuclear spins and exchange interactions,the effective spin Hamiltonian of these interactions is usually written as

where HZeis Zeeman effect operator,HZFSis zero-field splitting operator,βBis the Bohr magneton,B is the magnetic flux density,S is the effective spin operator,and g and D are the g-tensor and ZFS-tensor,respectively.Hspinacts on the basis functions｜SM〉with M=S,S-1,…,-S.If we choose a coordinate system that diagonalizes D,HZFScan be rewritten:

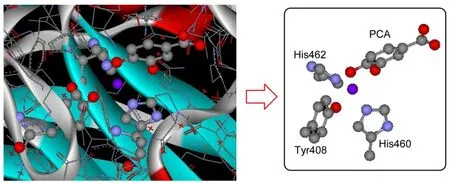
Scheme 1 Active-site geometric structures of 3,4-PCD-PCA(PDB code 3PCA)

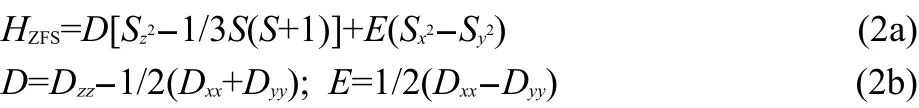
Thus,the ZFS is uniquely defined by the parameters D and E and the tensor orientation.Typically,D and E/D are given in a coordinate system that fulfils the following condition:

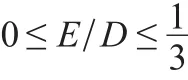
DFT calculations of the ZFS were carried out using qausirestricted theory11by the ORCA program.12Previous studies11have investigated the dependences of the g-tensor and ZFS on the exchange-correlation functional.Thus,in this work,we obtain ZFS parameters(D and E)from additional single-point calculations using 6-311G(d)basis sets and the BP86 GGA functional.We use a recently described SOC operator that efficiently implements a spin-orbit mean-field(SOMF)method.16

2.3 Spin-orbit coupling and exchange coupling calculations

Exchange coupling constants(J)are calculated using the Yamaguchi formula,which covers consistently the whole range of situations from the strong to the weak exchange coupling limit:17,18

where EHSand EBSaccount for the energies of the high-spin and broken-symmetry states,respectively;〈S2〉HSand〈S2〉BSdenote the spin angular momentum calculated in the high-spin and broken-symmetry solutions,respectively.These calculations were performed with a development version of the ORCA program.12

In addition,in order to obtain the more detailed SOC matrix elements,the SOC calculations of the sextet and quartet states were studied using the approximate one-electron spin-orbit Hamiltonian(hi)13given in Eq.(4):

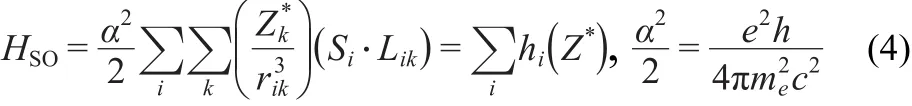
where Likand Siare the orbital and spin angular momentum operators for electron i in the framework of the nuclei indexed k,respectively,andZ*kis the effective nuclear charge,rikis the distance of between each electron samples(i)and all nuclei(k).One-electron SOC calculations were carried out using the GAMESS program.19

3 Results and discussion

3.1 Initial complex electronic states

The optimized geometries and energetic data for the octet,sextet,and quartet electronic states are depicted in Fig.1,in order to keep the discussion more simple,the goal complex,denoted as 1,is initially formed as 3,4-PCD-PCA and O2collide end-on with each other,where the superscripts denote the spin multiplicities(81,61,and41).

3.1.1 Octet state(S=7/2)

The singly occupied molecular orbitals(SOMOs)of81 are plotted in Fig.2 and It clearly shows that O2has two unpaired electrons,O2π*(y)and π*(z),while five others reside on the ferrous Fe(III)center,namely occupy five d orbitals,thus forming a high-spin(HS)Fe(III)(S=5/2)combined ferromagnetically with a triplet O2(S=1).Therefore the octet81 is approximately understood as van der Waals complex,which involves O2in a end-on orientation with a long Fe―O bond length of about 0.2558 nm at the U-B3LYP/LanL2DZ level(0.2487 nm for U-BP86/6-311G*),as shown in Fig.1.

3.1.2 Sextet state(S=5/2)

We obtained a sextet61 complex as shown in Fig.1.Compared with81,the Fe―O bond length was shortened to 0.1906 nm for U-BP86/6-311G*,while the O―O bond length was increased to 0.1281 nm.These show that O2and Fe center has obvious chemically bonded effect in the sextet61 complex.The electronic structure of61 is schematically shown in Fig.3.It is seen that O2is a superoxide,having a singly occupied O2π*(y),which is vertical to the Fe―OO plane,while the other doubly occupied π*(z)[π*(z)is in Fe―OO plane]forms a two-electron bond with the iron dz2orbital.61 has an ferromagnetically coupling of the S=1/2 superoxo anion O-2with S=2 Fe(IV)center.81 as zero reference,the U-BP86 calculated relative energy of61 is-12.14 kJ·mol-1.

3.1.3 Quartet state(S=3/2)

For the quartet state41,in contrast with the sextet61 case,one pronounced difference is that the Fe(IV)center has two singly occupied orbitals(dxyand π*xz,S=1),that is,41 differs from61 by a spin-flip of the a singly occupied orbital from σx2-y2to dyz,consequently,dyzis doubly occupied.O2(S=1/2)is still a superoxide with a singly occupied π*(y)and a doubly occupied π*(z)orbitals,and coupled ferromagnetically with the Fe(IV)(S=1),thus formed an intermediate-spin S=3/2 complex,41.The U-BP86 calculated energy difference is 9.21 kJ·mol-1relative to the61 state.

3.2 Intersystem crossing process of initial complexes

As has been already discussed before,the triplet O2(S=1)mixes with Fe(III)(S=5/2)resulting in the different spin states with a total spin of S=7/2,S=5/2,or S=3/2,and smaller energy differences among them.Moreover,we found that the spin states from the octet to quartet state are changed with the decrease of the Fe―O bond length(from 0.2487 to 0.1895 nm at the U-BP86/6-311G*level),and the sextet61 is the most stable as shown in Fig.4.In this respect,the interesting question is raised:how is the intersystem crossing of the different spin states happened?

3.2.1 Exchange coupling(J)

Fig.1 Selected bond lengths(nm)and energies(listed under the structures)obtained from the key point optimizations at the U-BP86/6-311G(d)and U-B3LYP/LanL2DZ levels(in the parentheses)

Let us turn to discuss this question now,starting from the octet state81.To identify some main atomic orbital interactions,the main antiferromagnetic orbital interactions of81 were also inferred from overlaps calculated from the broken-symmetry wave function(U-BP86/6-311G*),the results calculated are plotted in Fig.5.In general,the broken-symmetry orbitals of different spin indexes(i.e.,α or β)are not orthogonal to each other and are localized on Fe(ϕiα)or O2(ϕjβ).Therefore,to this extent,the overlaps Sij=〈ϕjα｜ϕjβ〉are intimately related to the strength of antiferromagnetic spin coupling.As seen from Fig.5,the overlap between the localized Fe dz2and O2π*(z),129α and 129β,is considerably better and Sij=〈129α｜129β〉=0.3758 at the Fe―O distance of 0.2487 nm.The low spin coupling between 129α and 129β electron pair is therefore strong enough to lead to a Fe―O bonding.By contrast,the other overlap S=〈130α｜130β〉of the Fe dyzand O2π*(y)is much weaker and Sij=0.0868.Thus the magnitude of the overlaps strongly suggested that the first Fe dz2:O2π*(z)was clearly dominant ex-change pathway,whereas Fe dyz:O2π*(y)contributed to a lesser extent and was fairly comparable.At the same time,we found that the overlaps are increased with the decrease of the Fe―O bonding,and the change of the exchange coupling constant J is very similar to that of the overlaps,the J values are increased from-20.8 to-81.4 cm-1with the distance of the Fe―O bonding from 0.2487 to 0.2200 nm.These calculations provided a detailed approximation to antiferromagnetism induced by Fe dz2:O2π*(z)delocalization.

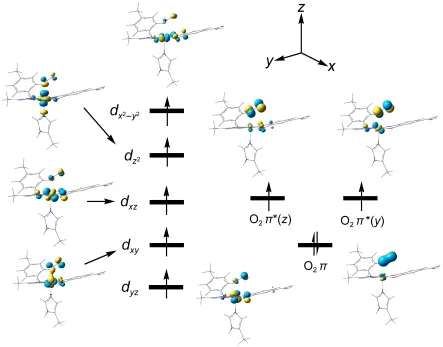
Fig.2 Electronic configuration of the octet state81

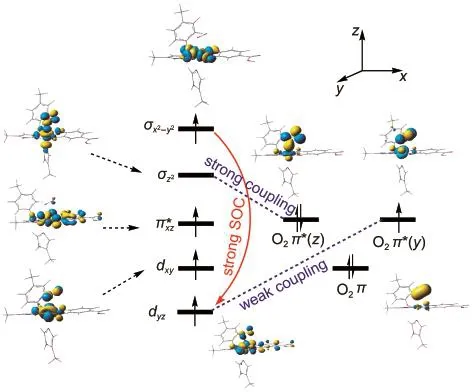
Fig.3 Occupied active natural orbitals of61 at the BP86/6-311G(d)level

Fig.4 Schematic representation of calculated reaction paths at the B3LYP/LanL2DZ level

Therefore the formation of61 from81 is most likely due to the electron exchange induced enhanced intersystem crossing(EISC).20Certainly,for antiferromagnetic exchange,the energy gap between61 and81 is also very important.The energy gap between these two states is about 12.14 kJ·mol-1,one might expect that EISC would be faster.The electron exchange interaction between Fe(III)(S=5/2)and O2(S=1)serves as the first-order perturbation that drives EISC.The magnitude of this perturbation,and thus the overall intersystem crossing rate,depends strongly on the electronic overlap between the orbitals that contribute to the singly occupied molecular orbitals(SOMO)of the Fe(III)(S=5/2)center and O2(S=1).

In addition,antiferromagnetic exchange coupling can lead to the partly forming of41 due to the weaker overlap S=〈130α｜130β〉.We also noted that the quartet wave function can have some admixture of the sextet wave function.The effect was more noticeable,the expectation value of the total spin operator after annihilation,〈S2〉=5.47 was far from the value expected for a pure quartet state,〈S2〉=3.75.Based on the following expressions for the spin expectation values of the contaminated quartet state:18

where C is the configuration coefficient,S is the total spin operator,subscripts 6 and 4 denote sextet state and quartet state,respectively.From Eq.(5)we obtain the contribution of the quartet state which is about 67%of the mixing states.This reason is that a second-order term of ZFS,SOC)introduces some angular momentum into the sextet state.These mechanisms above are described in Fig.3.

3.2.2 Zero-field splitting(ZFS)

Fig.5 Pathways of the exchange coupling from81 to61 or41

The net effects for ZFS are to introduce a splitting of the 2S+1,in the absence of an external magnetic field.This will main-ly attribute to the ZFSʹs two contributions:11(a)a first-order term,the direct dipolar spin-spin(SS)interaction between pairs of electrons and(b)a second-order term,arising from SOC.Thus an analysis and interpretation of the ZFS is imperative in this study.

BP86 calculations were performed to determine the signs of the D and E values for61.The ZFS parameters[D=Dzz-1/2(Dxx+Dyy),E=1/2(Dxx-Dyy)]are calculated,D=+8.589 cm-1and E/D=+0.068.The more detailed results of the calculated ZFS using the quasi-restricted DFT method are shown in Table 1.From the results in Table 1,the major contribution arises from the second-order SOC contribution(around 97.5%of D),while the SS contributions are essentially negligible.Concerning the SOC part,it contains four significant contributions:α→α(D=0.332 cm-1),β→β(D=0.240 cm-1),α→β(D=8.138 cm-1),and β→α (D=-0.336 cm-1).However the major contribution comes from the α→β spin-flip excitation.This excitation contributes around 77.2%of the DSOCvalue,corresponding to the spin-pairing ΔS=-1(i.e.,sextet→quartet)transitions.The second larger SOC contribution arises from the β→α spin-raising ΔS=+1(sextet→octet)excitation(around 4%of DSOC)corresponding to ligand-to-metal charge-transfer transitions.The remaining two SOC contributions come from the spin allowed ΔS=0(sextet→sextet)ligand-field excitations and have usually been solely held responsible for the ZFS.However,these contributions are only around 7%compared to the DSOCvalue.

The ΔS=-1 state(sextet is flipped to quartet state)is found to make significant contributions to DSOC,with the primary contribution arising from the single-determinant spin-paired states within the single occupied sets of orbitals,σx2-y2,π*xz,dxy,and dyz(see Fig.3).Namely,andvital spin-flip excitation.Applying the angular momentum operator to this four orbitals generates three nonzero SOC integrals:ndlz｜dxy〉which make the largest contribution to the SOC and lead to the larger values of Dxx(=8.8 cm-1),Dzz(=16.8 cm-1),and Dyy(=7.6 cm-1).It identifies the origin of large ZFS as spinorbit coupling to low-lying ΔS=-1 state,and shows that the quartet41 can arise from normal spin-orbit induced intersystem crossing as compared with the weaker exchange coupling.

3.2.3 Spin-orbit coupling

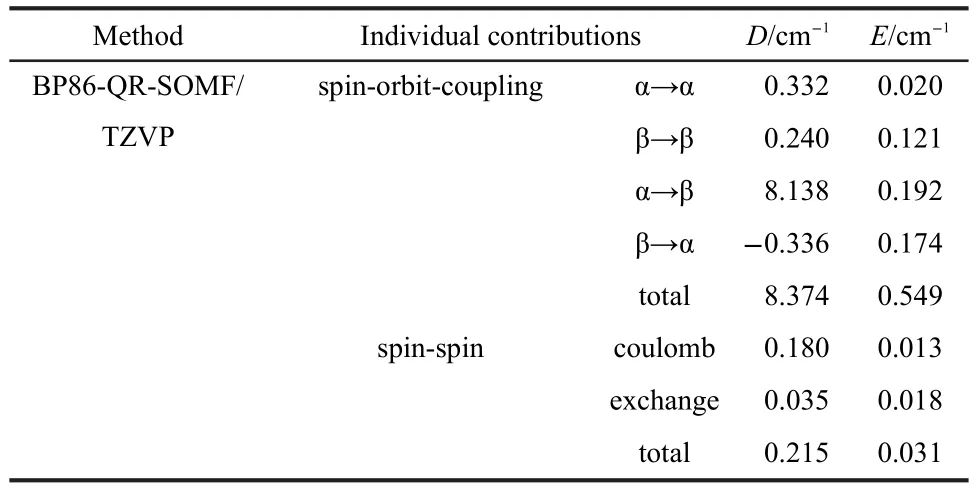
Table 1 Contributions to the calculated zero-field splitting between spin-orbit coupling and spin-spin for the sextet state

Based on the above analysis,the sextet61 from81 is fast formed via EISC,following the system will well change its spin multiplicities from the sextet state to the quartet ground state41 by SOC in the O2gradual approach to Fe center process.However,a spin-forbidden transition requires an effect of SOC that provides a major mechanism for the intersystem crossing process.21-24Therefore,we must inspect the orbital relationships which promote the SOC matrix elements.

The ROHF orbitals for the construction of the quartet and sextet CASCI wave functions to be used in the SOC evaluation have been generated by the sextet ROHF calculation.At the CAS(7,6)level the dominant determinants of the MCSCF wave functions have configuration interaction(CI)coefficients of 0.98 and 0.17 for the sextet and 0.86 and-0.48 for the quartet state(configurations of less than 0.1 have not been listed).Thus the permissible approximation of the sextet wave function by a single configuration(0.98)enables us to analyze the SOC matrix elements.The quartet configuration is described as shown in Eq.(6),

Nonzero elements of the p-components(p=x,y,z)of the SOC matrix,,are always proportional to the function,Fp,as given in Eq.(7).

To further understand the efficient SOC,it is very important that the SOC matrix elementsandare discussed.Because the SOC constant(ξFe)is an order of magnitude greater than that of oxygen,making it a reasonable approximation to consider only the Fe contribution when discussing spin-orbit mixing with quartet states.Thus

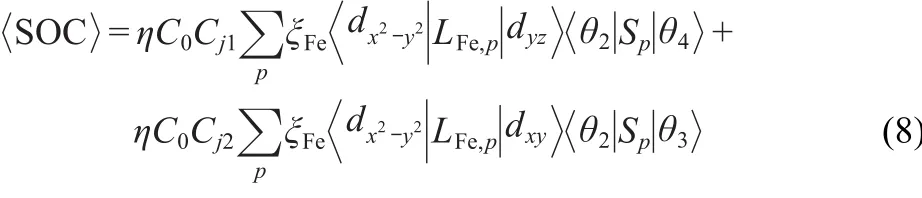
where the η term is the MS-depended weight weighing factor,and θ=α and/or β.In the present case,for the sextet state,the fundamental open-shell configuration has one dominant coeffi-cient,i.e.,C0=0.98≈1,while coefficients of quartet states are Cj1=0.86 and Cj2=-0.48,respectively.

Table 2 Calculated SOC matrix elements(cm-1)in the41 structure

Fig.6 Electronic evolution during the O―O bond cleavage

Therefore:

Here,only the first term is nonzero value,the electron shift from dx2-y2to dyzcreates an non-zero angular momentum in the Lx-direction,resulting in the larger SOC matrix elements as listed in Table 2.The second term is zero value due to the mismatch for the dx2-y2→dyztransition with Lzangular momentum direction.Similarly,the larger z-direction SOCs come from〈dx2-y2│LFe,z│dxy〉〈α│Sz│α〉coupling of the second term in Eq.(9).These analyses are in good agreement with the SOC calculations of the approximate one-electron spin-orbit Hamiltonian(see Table 2)and D-tensor of ZFS,25namely there exist the larger SOC matrix elements in Lx-and Lz-directions,resulting in the SOC constant of 353.16 cm-1.These also further indicated that the significant contributions to D arise from the ΔS=-1 spin-flip transition,and the quartet state41 is produced by a spin-orbit coupling intersystem crossing.

3.3 Cleavage process of the O―O bond

Structural parameters of the transition state(4TS)on the quartet surface are collected in Fig.1.The O―O bond cleavage pathway is shown in Fig.6.The O―O bond activation takes place through a precursor intermediate42 and transition state(4TS),to afford a cleavage product4P.The4TS has the feature of partially broken O―O bond(0.1687 nm),in which the activation barrier is 111.37 kJ·mol-1with respect to42.4TS is characterized as a transition structure by one imaginary frequency of 839.7i cm-1,and the vibrational vector corresponds to the expected components of the reaction coordinate,i.e.,breaking of the O―O bond.

Schematic of the frontier molecular orbitals which participate in the three-electron transfer process upon the O―O bond cleavage is shown in Fig.6.As can been seen from Fig.6,the doubly occupied PCA π orbital is the HOMO in the complex,one electron from the doubly occupied PCA π orbital can be donated directly to the O2π*orbital to form the distorted O―CPCAbond.Two electrons are transferred to the O2π*orbital generating a Fe(IV)-peroxide.There is the strong covalent interaction between the PCA HOMO and Fe dxzorbitals in the α manifold,the second electron of the PCA HOMO is transferred to Fe,at the same time the transfer of an Fe d electron into the O2σ*orbital to break the O―O bond is accomplished.Finally,cleavage of the O―O bond leads to formation of an Fe(IV)-oxo.Therefore,the transfer of these three electrons(one α and two β)shows that the Fe center acts as a buffer to transfer an electron pair from PCA π orbital to the triplet O2in the spin forbidden reaction.

4 Conclusions

The O2activating mechanism by non-heme iron enzyme,3,4-PCD-PCA,has been studied using theoretical calculations.The electronic structure origins and intersystem crossing of the different spin states(a total spin of S=7/2,S=5/2,or S=3/2)were discussed by the broken-symmetry method and SOC mechanism.The octet state81 is stable with the aid of the electrostatic interaction,while the ultrafast formation of61 is most likely due to EISC.As for the formation of the quartet state41 from the sextet61,there coexist the two effects,electron spin exchange coupling and spin-orbit coupling in the sextet61.As a driving force of spin conversion the exchange interaction competes with spin-orbit coupling interaction.The calculated results show that the latter is the dominant factor due to the larger SOC constant(353.16 cm-1).The doublet21 optimization is failure using various DFT methods,all optimizations can not be converged due to the energy fluctuation.

The O―O bond activation takes place through a precursor intermediate42 and transition state(4TS),to afford a cleavage product4P.The electronic transfer of the PCA HOMO is the vital role for the cleavage of the O―O bond.The Fe center of non-heme enzyme is a buffer to transfer an electron pair from PCAHOMO orbital to the O2in the reaction.

(1)Pau,M.Y.M.;Davis,M.I.;Orville,A.M.;Lipscomb,J.D.;Solomon,E.I.J.Am.Chem.Soc.2007,129,1944.doi:10.1021/ja065671x

(2) Costas,M.;Mehn,M.P.;Jensen,M.P.;Que,L.,Jr.Chem.Rev.2004,104,939.doi:10.1021/cr020628n

(3) Solomon,E.I.;Brunold,T.C.;Davis,M.I.;Kemsley,J.N.;Lee,S.K.;Lehnert,N.;Neese,F.;Skulan,A.J.;Yang,Y.S.;Zhou,J.Chem.Rev.2000,100,235.doi:10.1021/cr9900275

(4) Nam,W.Accounts Chem.Res.2007,40,522.doi:10.1021/ar700027f

(5) Borowski,T.;Siegbahn,P.E.M.J.Am.Chem.Soc.2006,128,12941.doi:10.1021/ja0641251

(6) Deeth,R.J.;Bugg,T.D.H.J.Biol.Inorg.Chem.2003,8,409.

(7) Fiedler,A.;Schroder,D.;Shaik,S.;Schwarz.H.J.Am.Chem.Soc.1994,116,10734.doi:10.1021/ja00102a043

(8)Yoshizawa,K.;Shiota,Y.;Yamabe,T.J.Chem.Phys.1999,111,538.doi:10.1063/1.479333

(9) Shaik,S.;Hirao,H.;Kumar,D.Accounts Chem.Res.2007,40,532.doi:10.1021/ar600042c

(10) Schroder,D.;Shaik,S.;Schwarz,H.Accounts Chem.Res.2000,33,139.doi:10.1021/ar990028j

(11) Neese,F.J.Am.Chem.Soc.2006,128,10213.doi:10.1021/ja061798a

(12) Neese,F.ORCA,version 2.8-20;Max-Planck Institute for Bioinorganic Chemistry:Mülheim an der Ruhr,Germany,2010.

(13)Fedorov,D.G.;Koseki,S.;Schmidt,M.W.;Gordon,M.S.Int.Rev.Phys.Chem.2003,22,551.

(14) Elgren,T.E.;Orville,A.M.;Kelly,K.A.;Lipscomb,J.D.;Ohlendorf,D.H.;Que,L.,Jr.Biochemistry 1997,36,11504.doi:10.1021/bi970691k

(15) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03,Revision E.01;Gaussian Inc.:Pittsburgh,PA,2003.

(16)Hess,B.A.;Marian,C.M.;Wahlgren,U.;Gropen,O.Chem.Phys.Lett.1996,251,365.doi:10.1016/0009-2614(96)00119-4(17) Rodriguez,J.H.;McCusker,J.K.J.Chem.Phys.2002,116,6253.doi:10.1063/1.1461363

(18)Rodriguez,J.H.;Wheeler,D.E.;McCusker,J.K.J.Am.Chem.Soc.1998,120,12051.doi:10.1021/ja980917m

(19) Schmidtm,M.W.;Baldridge,K.K.;Boatz,J.A.;Elbert,S.T.;Gordon,M.S.;Jensen,J.H.;Koseki,S.;Matsunaga,N.;Nguyen,K.A.;Su,S.J.;Windus,T.L.;Dupuis,M.;Motgomery,J.A.J.Comput.Chem.1993,14,1347.

(20)Giacobbe,E.M.;Mi,Q.;Colvin,M.T.;Cohen,B.;Ramanan,C.;Scott,A.M.;Yeganeh,S.;Marks,T.J.;Ratner,M.A.;Wasielewski,M.R.J.Am.Chem.Soc.2009,131,3700.doi:10.1021/ja808924f

(21) Isobe,H.;Yamanaka,S.;Kuramitsu,S.;Yamaguchi,K.J.Am.Chem.Soc.2008,130,132.doi:10.1021/ja073834r

(22)Dede,Y.;Zhang,X.;Schlangen,M.;Schwarz,H.;Baik,M.H.J.Am.Chem.Soc.2009,122,114.

(23)Lv,L.L.;Wang,Y.C.;Wang,Q.;Liu,H.W.J.Phys.Chem.C 2010,114,17610.

(24) Lü,L.L.;Wang,Y.C.Acta.Phys.-Chim.Sin.2006,22,265.[吕玲玲,王永成.物理化学学报,2006,22,265.]doi:10.3866/PKU.WHXB20060302

(25)Lü,L.L.;Zhu,Y.C.;Wang,X.F.;Zuo,G.F.;Zhao,S.R.;Guo,F.;Wang,Y.C.Chin.Sci.Bull.2013,58,627.[吕玲玲,朱元成,王小芳,左国防,赵素瑞,郭 峰,王永成.科学通报,2013,58,627.]doi:10.1007/s11434-012-5316-7