类比推理一例

江苏省镇江中学 陆建根 （邮编：212017）

推理与证明是新课程标准中新增的内容.在本章中，要求学生结合已学过的数学实例和生活中的实例，对合情推理、演绎推理以及数学证明的方法进行概括与总结，体会合情推理、演绎推理以及数学证明在数学结论发现、证明与数学体系建构中的作用.这样处理是为学生进一步加深对推理与证明的理解，掌握推理与证明的基本方法，提高数学思维的能力，形成对数学较为完整的认识.而要真正加深学生对这些内容的理解，关键在于教师在平时的教学中能抓住典型的例题进行深刻的剖析，引导学生去探究，去经历数学发现的过程，从而掌握数学发现的基本方法，发展学生的创新意识和创新能力.

现以苏教版必修4《平面向量》2.2.3“向量的数乘”例4为例，运用类比推理作适当的推广，供参考.

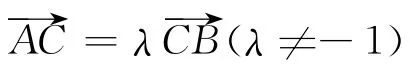
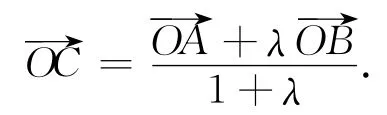
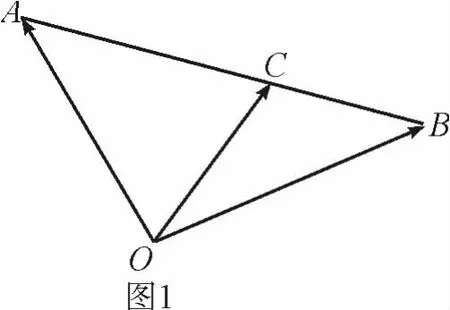
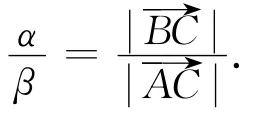
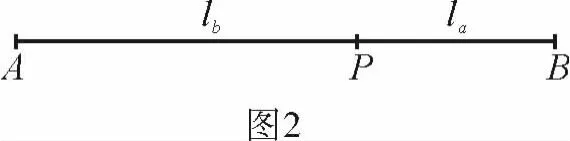
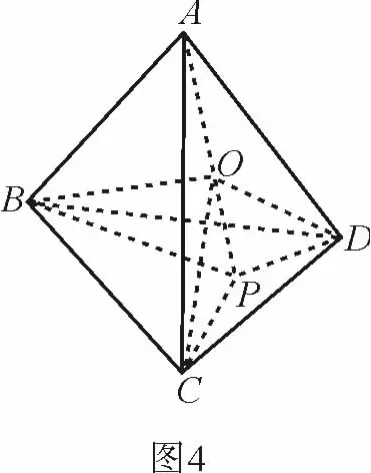
特别地，当O与C重合时，记为点P，如图2，

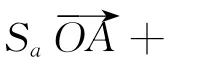
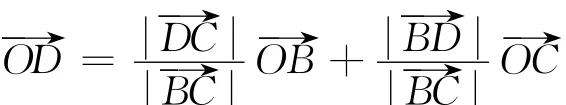
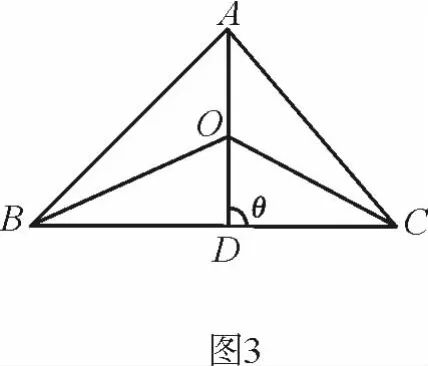
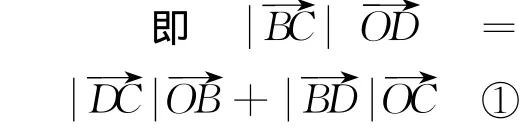
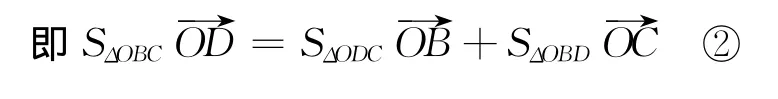
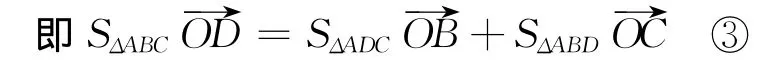
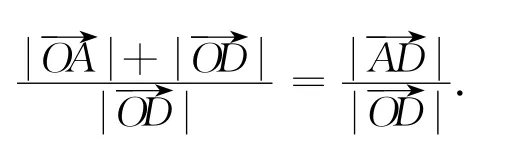
而上式显然成立，所以结论成立.

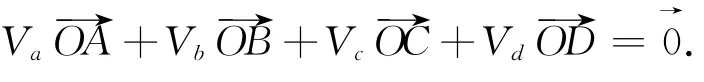
证明 延长AO交平面BCD于P，连结PA、PB、PC，设PA与平面BCD所成的角为θ，则由推广2知

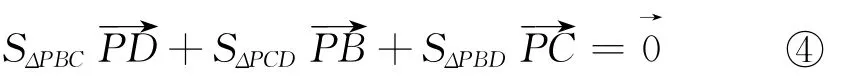
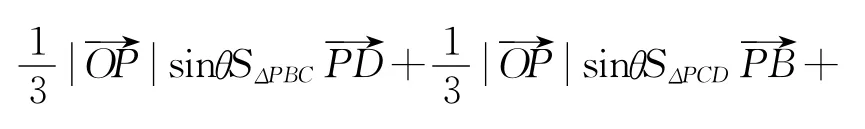
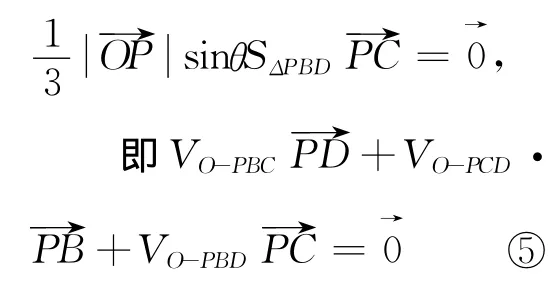
④式两边同乘以

上式显然成立，所以结论成立.

上述类比推理把线性的性质推广到平面、空间，这是结论的类比，而且证明方法也是层层推进，一脉相承，所以也是方法的类比.

由推广1可以得到的以下性质：

设a、b、c是ΔABC的 ∠A、∠B、∠C所对的边，若点P是ΔABC内一点，ΔBPC、ΔAPC、ΔAPB的面积分别记为Sa、Sb、Sc则：

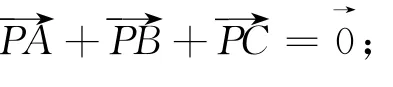
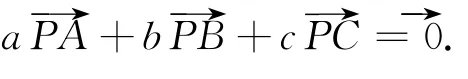
类比上述结论，我们可以得到推广2的若干性质：

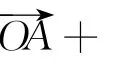
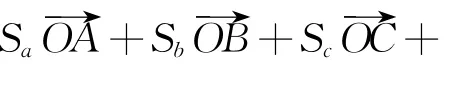
数学学习的目的不仅仅是记住几个公式，会做几道题目，而是要发展学生的数学思维能力.教材的很多内容是教师培养学生推理能力的很好的素材，关键在于我们老师如何去发掘.教师不要跟学生一起在茫茫题海中去捞题，而是要在学生匆匆做题时带着学生停下来，去想一想，悟一悟，一起做些探究.若能有所发现，则学生对原有知识的理解会上一个台阶，哪怕没有新的发现，对学生的创新意识、创新能力的培养也是一个锻炼.

1 单墫.普通高中课程标准实验教科书数学选修2－2［M］.江苏：江苏教育出版社，2010

2 高中数学教学参考书数学选修2－2［M］.江苏：江苏教育出版社，2010

3 林国夫.三角形“四心”的向量特征及应用［J］.数学通报，2010