基于遗传算法的结构主动控制作动器优化布置*

毛克阳，孙作玉，燕乐纬，王 晖

(广州大学土木工程学院，广东广州 510006)

主动控制是应用现代控制理论［1］，对结构动力响应进行控制的有效措施。通常应用较多的作动器可以达到更好的控制效果，所带来一些不利的影响包括:需要有足够的能源保障，这使得控制系统成本提高;对控制系统的可靠性提出了更高的要求;同时主动控制算法相对复杂，因此高效、优化的算法才可达到理想的控制效果。为了兼顾控制效果和控制成本，主动控制中作动器的优化布置是一个十分重要的问题，即当作动器数量限定的条件下，对其安装位置进行优化配置。目前，针对该问题常用的方法有试错法和穷举法，前者一般得到的是局部最优解，后者仅适用于设计空间较小的系统。遗传算法 (Genetic Algorithm，GA)是一种仿生学最优搜索方法，其简洁的二进制编码 (0，1编码)可用于主动控制中作动器位置的编码表达，为此本文提出了相应的遗传算法优化方案，并针对不同控制目标函数，研究了作动器的优化布置。分析表明，所提方法具有高效、便捷的特点。

1 线性二次型高斯最优随机振动控制

线性二次型高斯最优控制 (Linear Quadratic Gaussian optimal control，LQG)作为一种成熟、高效的控制算法已经被成功应用于结构的振动控制研究［2］，算法核心是对Riccati方程进行求解。钟万勰［3］提出的状态空间控制理论运用精细积分方法来求解Riccati方程，将矩阵指数的计算提高到了计算机精度。此外，对实时控制系统部分信息参数的求解，可以提前离线计算，储存起来用于后续调用，大大提高了计算效率。

1.1 LQG状态空间控制算法

动力状态方程为:

量测输出:

式中，A、Bu、C、D和Bw分别为系统特性矩阵、控制力位置矩阵、测量矩阵、直接传递矩阵和干扰力位置矩阵，x为状态向量;w为输入的随机激励荷载。则最优控制问题就是设计最优控制力u使二次型性能指标符合下列条件:

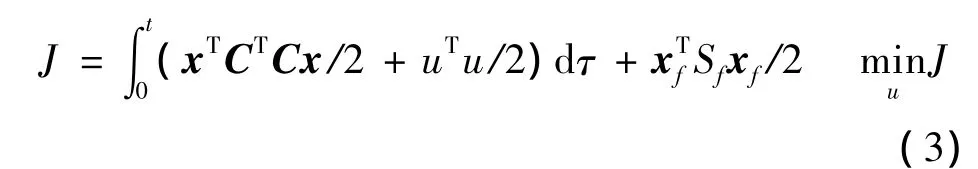
对上式 (3)采用Lagrange乘子函数解除状态方程式 (1)的约束条件，并结合Hamilton体系的变分原理，最终转化为求解下式Riccatti微分方程:

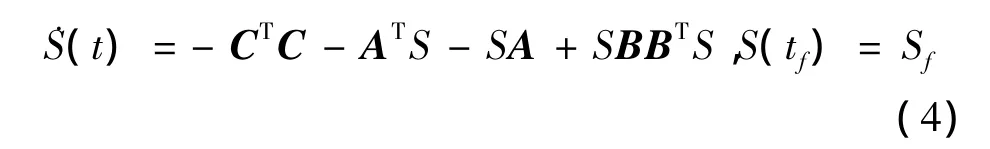
对于w为随机荷载激励控制系统，状态向量x为随机过程，其值可利用状态空间精细积分方法求解下式微分方程得到:

其中，S即为Riccatti微分方程式 (4)的解。

1.2 等效随机激励荷载

传统随机振动分析方法计算复杂，应用于结构振动控制系统的研究较少。近年来，虚拟激励法的提出及应用大大提高了随机振动分析的计算效率［4］，且仍保留了足够的精度。在此基础上发展起来的等效激励法［5－6］，通过构造等效激励，仅需一次动力响应分析及Fourier分解即可计算出结构的动力响应，进一步提高了随机振动的计算效率。

采用指定场地条件下的Kanai-Tajimi谱生成随机激励荷载:

式中，ω为地基土的卓越周期，ζg为地基土的阻尼比，S0为地震谱强度因子。

采用上述功率谱(w)作为随机激励荷载，令 ω∈［ωa，ωb］，ωa=0.01 Hz，ωb=20 Hz。基于等效激励法，构造等效随机激励荷载:

式中，H(ωK)为结构的传递函数，反应了结构的动力特性。将进行Fourier分解，可以求得某频率下的结构响应:

将 (7)式构造的等效荷载作为激励求解结构动力响应，即可实现相应的随机振动分析。

2 遗传算法设计

遗传算法自1975年由John Holland［7］首次提出以来，凭借其广泛的适用性、隐含并行性、以及全局寻优能力强的特点，被国内外学者广泛应用［8－10］。

2.1 编码

采用二进制{0，1}编码方案，通过改变编码来调整状态方程中控制力位置矩阵Bu，从而达到智能优化的目的。令n层结构中，作动器布置的代码向量为:

r(i)=［e1，e2，e3，…，ej，…en］第i个染色体

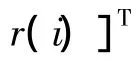
2.2 种群初始化

对n个设计变量的优化问题，种群初始化的步骤为:确定种群规模M;确定个体位串长度L;随机产生指定位串长度的个体;重复上一步操作，直至产生规模大小为M的种群。

2.3 适应度评价函数

层间位移角是反映结构安全性的主要因素，楼层加速度则主要体现结构的舒适性。综合考虑以上两种因素，采用受控结构在随机地震激励作用下最大层间位移角、最大楼层加速度与结构无控状态下响应反应量比值的无量纲线性组合作为目标函数。优化的最终目的是目标函数值取最小［11］。

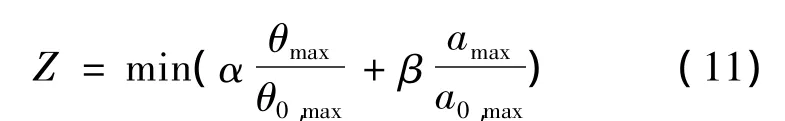
式中，θmax和θ0，max分别为结构在有控和无控地震作用下的最大层间位移角;amax和a0，max分别为结构在有控和无控地震作用下的加速度最大值。α，β分别为加权系数。

2.4 遗传算子

遗传算法操作过程中选择算子对群体进行优秀个体的筛选，交叉算子通过交换重组产生了新的子代，变异算子的实施保证了群体基因的多样性，精英策略则确保了代内最优个体的保留。本文中，选择算子——竞标赛选择法，交叉算子——单点交叉，变异算子——两点变异，精英保留策略——每次迭代遗传操作完成后，均把该代内最优的个体保留下来。

3 算例分析

针对某20层钢结构建筑，总高72 m，层高3.6 m。各楼层质量及水平侧移刚度信息如下表1所示，结构阻尼比为0.05，建筑场地为Ⅳ类场地土，抗震设防烈度为7度，设计地震分组为第一组。采用Rayleigh阻尼，按层剪切模型进行计算。作动器安装数目为10个。施加主动控制，对受控结构进行随机振动分析并对作动器进行优化布置。

表1 各层质量及水平侧移刚度值Table 1 Masses and horizontal stiffnesses

依据《建筑抗震规范》，7度设防，设计地震分组第一组时，Kanai-Tajimi谱参数分别为［12］:ωg=9.67 rad*m－1，ζg=0.9，S0=2.349*10－4m2s－3。见图1。

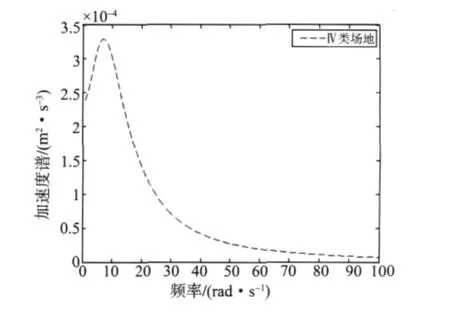
图1 Ⅳ类场地土条件下Kanai-Tajimi谱Fig.1 Kanai-Tajimi spectral on theⅣsites

遗传操作参数取为:种群规模20，个体编码位串长度20，最大迭代代数100，交叉概率0.8，变异概率0.2。适应度进化见图2。

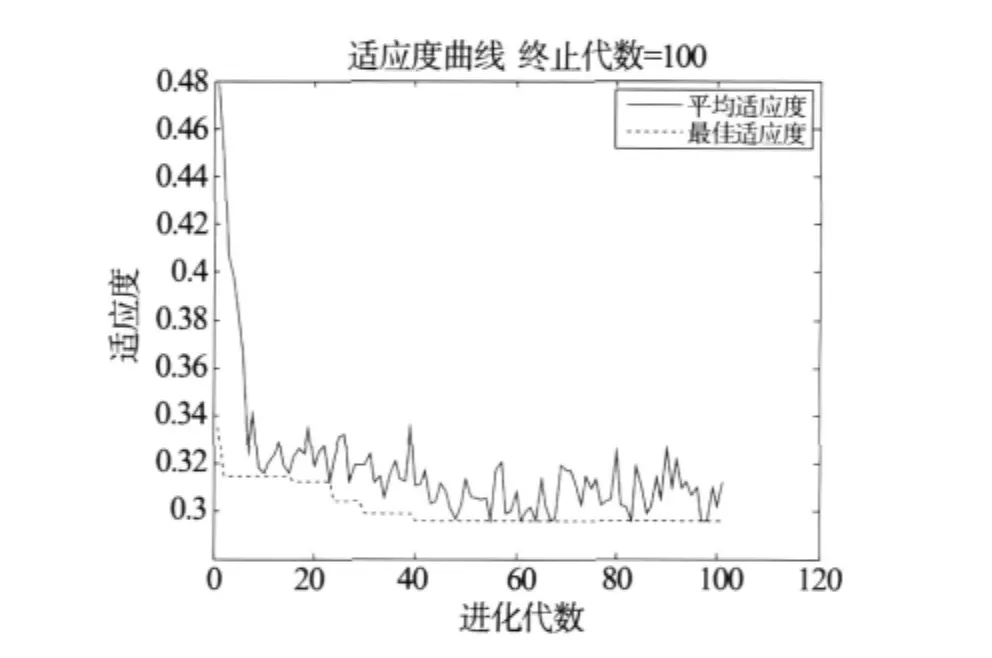
图2 α=1的加权目标函数优化结果Fig.2 Optimization results of the weighted objective function with α=1

Ⅳ类场地条件下，三种不同权值的组合目标函数作用下优化结果如表2所示，结构响应最大值分别如图3－6所示。

表2 不同目标函数控制下的优化结果Table 2 The optimization results of different objective functions

4 结论

1)针对该优化模型，经过近40代的迭代便找到了最优解，说明遗传算法的二进制编码方案在处理此类问题时的高效性。

2)不同的目标函数对应着不同的作动器布置方案，层间位移角主导的目标函数对作动器的要求偏于楼层全高度分布，加速度主导的目标函数对作动器的要求偏于楼层中上部分布。从结构整体响应来说，层间位移角比加速度对结构的控制效果更为合理。

3)本文利用等效激励法将随机振动分析由频域转换到时域进行计算，为随机振动分析提供了一种新的思路。

［1］阎维明，周福霖，谭平.土木工程结构振动控制的研究进展［J］.世界地震工程，1997，13(2):8 －20.

［2］欧进萍.结构振动控制——主动、半主动和智能控制［M］.北京:科学出版社，2003.

［3］钟万勰，吴志刚，谭述君.状态空间控制理论与计算［M］.北京:科学出版社，2007.

［4］林家浩，张亚辉.随机振动的虚拟激励法［M］.北京:科学出版社，2006.

［5］孙作玉，王晖.结构振动分析的等效激励法［J］.工程力学，2010(SI):20－22.

［6］TANG Yao，SUN Zuoyu，WANG Hui.Random vibration analysis of controlled building based on the equivalent excitation method［C］∥Information Technology and Architecture Engineering(ITAE 2012)，2012，4:456 －459.

［7］Holland J H.Adaptation in natural and artificial systems［M］.Ann Arbor，Michigan:University of Michigan Press，1975.

［8］燕乐纬，蹇开林，黄晓刚.基于广义遗传算法的结构动力响应优化［J］.工程力学，2008，25(7):57 －65.

［9］燕乐纬，陈树辉.基于改进遗传算法的非线性方程组求解［J］.中山大学学报:自然科学版，2011，50(1):9－13.

［10］燕乐纬，陈洋洋，周云.一种改进的微种群遗传算法［J］.中山大学学报:自然科学版，2012，51(1):50 －54.

［11］李宏男，曲激婷.基于遗传算法的位移型与速度型阻尼器位置优化比较研究［J］.计算力学学报2010，27(2):252－257.

［12］薛素铎，王雪生，曹资.基于新抗震规范的地震动随机模型参数研究［J］.土木工程学报，2003，36(5):5－10.