服务机器人变刚度关节驱动系统设计

林阿斌，周建军，张亚平

（杭州电子科技大学 机械工程学院，浙江 杭州 310018）

0 引 言

机器人的关节驱动系统是向执行系统各部件提供动力的装置。工业机器人的关节驱动系统采用高刚性的设计。高刚性的驱动系统可以保证执行机构的精确定位和其运行轨迹的精确跟踪，能高效率地实现重复执行的工作，但同时这使得工业机器人工作空间固定，工作模式死板。随着机器人技术的发展，机器人也从传统的工业领域里被解放出来，进入了其他非工业领域，如服务、医疗、娱乐等。其中服务型机器人与人的交互颇为紧密，人类工作环境的复杂多变，势必会对机器人提出严苛的要求，如高安全性、对未知环境良好的适应性和较高的能量利用率。

人类的运动通过肌肉骨骼系统实现。其中“肌肉”作为动力输出元件，本身具有可变刚度的特点。如当人要实现用针穿线等精确度很高的动作时，肌肉会处于紧绷状态，刚度较大，以提高位置控制精度；而当人步行时，手臂处肌肉处于松弛状态，刚度较小，以适应步态需要，减小能量消耗。为了满足上述要求，服务机器人关节驱动系统不能效仿工业机器人的设计特点—高刚性，而是要具有可变刚度的特性。

为了使机器人关节驱动系统具有可变刚度的特性，国外高校和机构做了大量的研究，并取得了一定的成果。其中具有代表性的是，意大利技术研究所（IIT），德国宇航局（DLR），比萨大学（Pisa University），布鲁塞尔自由大学（VUB），韩国大学（Korea University）。

IIT 的D.G.Caldwell 等人[1]研制开发了一种柔顺紧凑的驱动单元。该驱动单元是基于一种创新的弹簧组合设计研制而成的，预紧过的螺旋弹簧在辐条转动的时候，刚度成非线性变化，这使得整个模块刚度也成非线性变化。他们随后研制的AwAS-I/II（Actuator with Adjustable Stiffness-I/II）通过在与主驱动电机相连的一摆杆两侧设置一组预紧的弹簧，分别改变其有效臂长和力矩支点来改变刚度，以实现弹性模块的变刚度[2-3]。DLR 的G.Hirzinger 等人[4]提出了一种变刚度的关节VS-Joint（Variable Stiffness Joint），通过调节弹簧模组顶部的端盖来对弹簧组进行预紧。由控制刚度的小电机使滚子发生偏转，当滚子从凸轮底部向两侧移动时，弹簧压缩，系统刚度变大，反之亦然。之后，他们又在VS-Joint 基础上进行改进，提出了新的变刚度关节—FSJ（Floating Spring Joint）[5]，将原本弹簧模组中的3 根螺旋弹簧改为一根浮动弹簧，该弹性模块实现变刚度的原理与VS-joint 相似，也是借助滚子偏转实现的。

比萨大学的Antonio Bicchi 等人[6]采用带轮与弹簧的组合，设计研制了一种变刚度的驱动器VSA（Variable Stiffness Actuator）。驱动器有3 个带轮，其中的2 个带轮下方各有一个电机，用以控制带轮的旋转。当带轮旋转时，与之相对应的弹簧长度就会改变。这样，通过改变带轮的旋转的角度就可以改变VSA 的刚度。VUB 的Dirk Lefeber 等人[7-8]提出了基于机械结构可调刚度，平衡位置可控的柔顺驱动器（MACCEPA，Mechanically Adjustable Compliance and Controllable Equilibrium Position Actuator）。该项研究在关节处设置两个小型伺服电机，电机输出惰轮上分别连接一螺旋弹簧的两端，通过控制控制电机旋转来改变弹簧的预紧度，从而来改变关节旋转时的受力。韩国大学的Jae-Bok SONG 等人[9]提出了一种混合式双电机驱动单元，其中一个电机提供驱动力，另一个电机通过改变一对弹簧滑块的位置来控制单元刚度。当弹簧滑块远离输出旋转轴的旋转中心时，刚度变大，反之变小；其中弹簧滑块的顶部与杆件始终接触。

以上提到变刚度驱动器的特点可总结为：以线型螺旋弹簧为基础，配合特殊的结构设计，通过改变弹簧的伸缩量，致使弹性模块刚度发生变化，从而改变驱动系统的刚度。尽管达到了变刚度的目的，但由于其复杂的结构给设计带来了难度，线型螺旋弹簧的使用也势必会占据大量的空间，且维护困难。

本研究提出一种变刚度驱动系统，采用具有特殊几何结构的平面扭簧作为弹性模块，通过分析平面扭簧的刚度特性，得出其刚度与偏转角度的关系及刚度与预紧量大小的关系，为关节驱动系统进一步优化提供理论依据。

1 驱动系统的机械结构

本研究提出的变刚度驱动系统如图1（a）所示，该驱动系统由伺服电机、精密减速器、弹性模块、摆杆等组成。其中弹性模块的结构如图1（b）所示，由连接件一、平面扭簧、连接件二、轴承等组成。伺服电机得到控制信号后，开始工作并驱动减速器转动。

该系统在减速器的输出端有通过螺钉与之连接的连接件一，而平面扭簧则通过螺钉分别与连接件一和连接件二相连。减速器的转动带动连接件一起转动，力矩从伺服电机输出通过减速器传递到连接件一，并继续传递到平面扭簧的菱形段。菱形段受到扭转力矩的作用开始压缩，当力矩增大到与负载阻力矩相同时，平面扭簧开始转动，从而带动连接件二随之旋转，力矩从摆杆输出。

2 平面扭簧的刚度特性分析

此处弹性模块的变刚度特性是通过如图2（a）所示的平面扭簧实现的。下面笔者对该扭簧的结构特点及其力学特性进行分析，以得到扭簧刚度与偏转角度及扭簧刚度与预紧量之间的关系。

图1 变刚度关节驱动系统

2.1 扭簧刚度k 与偏转角度θ的关系

为了简化分析，本研究将图示扭簧的菱形段等效为一根变刚度弹簧，其刚度为ks(X)，简化后的模型图如图2（b）、2（c）所示。由于模型中的弹簧是两两对称的，取其中的一组分析。固定弹簧的一端，如图2（b）所示的m 点位置，转动θ后变为如图2（c）所示的状态。

图2 平面扭簧及其简化模型

假设 pm 的长度为a，op 的长度为r；转过θ后，弹簧的伸缩量为X，则可得到p'm'的长度为：

其中，X 可由下式来表达：

则图2（c）中所示的由于弹簧压缩产生的力大小为：

式中：F—一根弹簧产生的力。

片簧总共由4 组8 根弹簧组成，由于偏转角相同，即每根弹簧的伸缩量相同，均为x，可得片簧总的力矩为：

对式（4）进行处理，可得到片簧的刚度为：

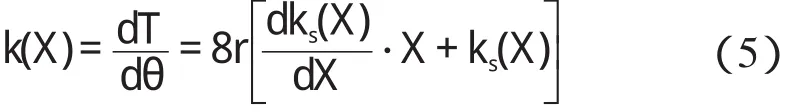
为了得到ks(X)的表达式，本研究将菱形段简化为如图3 所示的模型，并对其进行受力分析。

图3 菱形段简化模型及受力分析

由于模型为菱形结构，以MP 为中心轴，则两侧结构对称，可知其受力也对称，又由于该结构为超静定，M 点在F 力作用下，在水平方向没有位移，且没有转动。

本研究用力法可求解该超静定结构[10]，求得结果如下：

由此可知，如图3 所示的菱形段为一次超静定结构，点M 可以有竖直方向和水平方向的位移，但是不能有转动。利用叠加法，研究者可以求得在力F/2 和X2的联合作用下，点M 在竖直方向上的位移为：

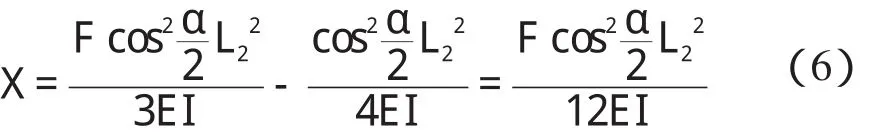
根据杆件的几何关系可以得到：

由式（6，7）可以得到F 与X 的关系式：

对式（8）进行处理，便可得到ks(X)的表达式：

根据式（5）即可得到：

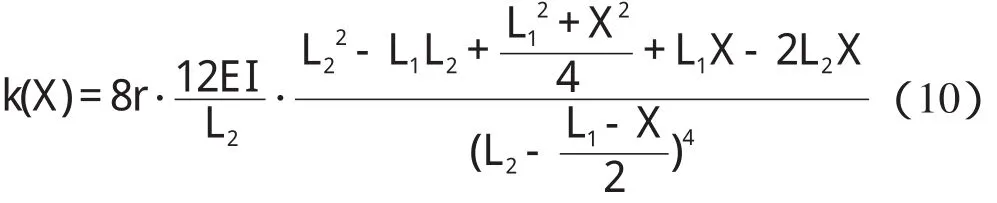
由式（2，9，10）可求出：

平面扭簧刚度k(θ)和菱形段刚度ks(X)随着偏转角度θ改变而变化的曲线如图4 所示。此时，平面扭簧的参数取值如下：

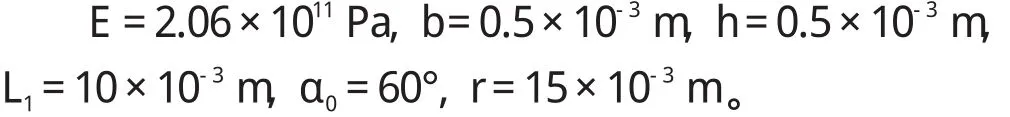
从图4 中可以看出，当偏转角度θ变大时，平面扭簧刚度k(θ)先逐渐变大，到θ=0.12 rad 附近时达到最大值，再逐渐变小，变化过程呈现非线性。

图4 刚度变化曲线

2.2 扭簧刚度k 与预紧量Δd 的关系

2.1 节中并没有考虑扭簧的预紧，实际上，扭簧可以通过菱形段中的通孔进行预紧，在与之相连的连接件一上，开有两个孔间距比扭簧上通孔间距稍大的螺纹孔，研究者将菱形段预压缩后，再通过螺钉进行固定，便可实现预紧。片簧预紧示意图如图5 所示，为菱形段预紧前后状态，设连接盘上的孔间距大小为D，片簧通孔间距为d，则得到预紧量为：

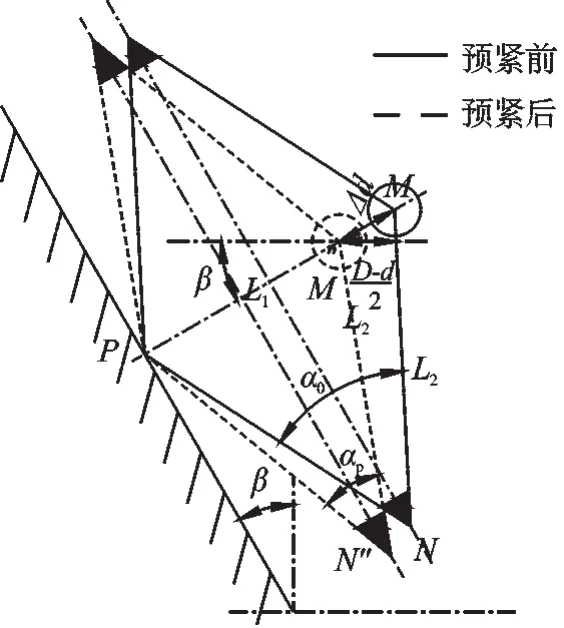
图5 片簧预紧示意图

从图5 的几何关系中可以得到，式（8，9）中的L1在经过预紧过后变为：

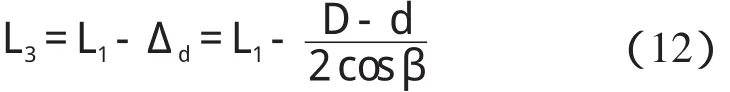
结合2.1 节中所得的菱形段的刚度ks(θ)，容易得到当预紧量为 Δd时，刚度 ksp(θ)和片簧刚度 kP(θ)为：

本研究对2.1 节中的扭簧进行预紧，按照预紧量大小的不同，做出的平面扭簧刚度kP(θ)随偏转角度θ的变化曲线如图6 所示。从图6 中可以看出，随着预紧量的增大，平面扭簧刚度也随之增大。

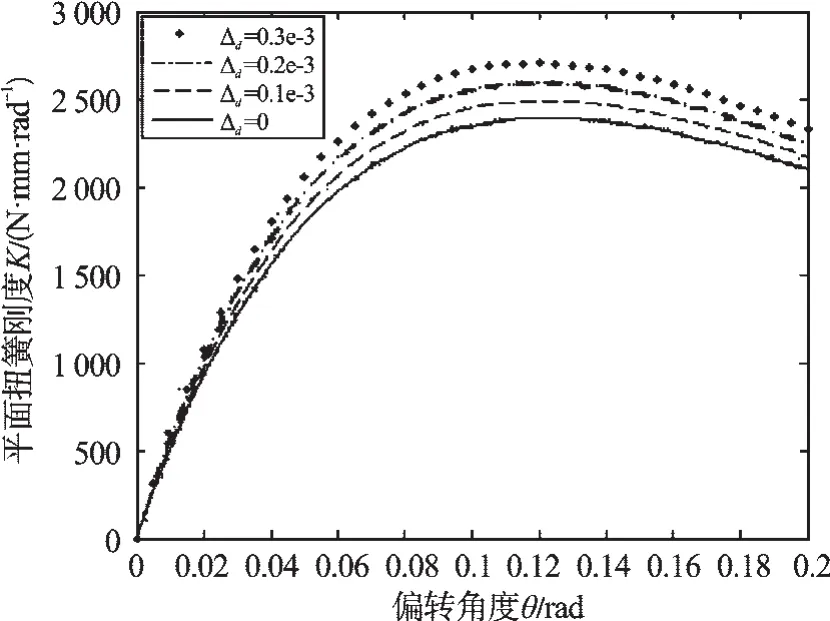
图6 平面扭簧刚度与预紧量大小的关系

至此，就得到了平面扭簧刚度与偏转角度及预紧量大小之间的关系。通过分析图6 可知，刚度根据预紧量改变而变化，变化范围大；且不论预紧量多少，平面扭簧刚度均在偏转角度θ=0.12 rad 处时，达到最大值。该平面扭簧最大偏转角度约为7 °，刚度变化范围大，可很好地满足机器人各个关节对刚度的不同需求。

3 结束语

为了使服务机器人具有高安全性、对未知环境有良好的适应性和较高的能量利用率以便其更好地融入人类社会，为人类的生活工作带来便利，研究者需要将原来沿袭于工业机器人的高刚性关节驱动系统设计变更为具有可变刚度的关节驱动系统。

本研究设计的关节驱动系统采用一种可通过改变偏转角度和预紧量大小以改变刚度的平面扭簧作

（References）：

[1]TSAGARAKIS N G，LAFFRANCHIM，VANDERBORGHT B，etal.A Compact Soft Actuator Unit for Small Scale Hu⁃man Friendly Robots[C]//International Conference on Ro⁃botics and Automation，2009：1998-2004.

[2]JAFARI A，TSAGARAKIS N G，VANDERBORGHT B，etal.A Novel Actuator with Adjustable Stiffness（AwAS）[C]//International Conference on Robotics and Automa⁃tion，2010：4201-4206.

[3]JAFARI A，TSAGARAKIS N G，CALDWELL D G.AwAS-II：A new Actuator with Adjustable Stiffness based on the novel principle of adaptable pivot point and variable lever ratio[C]//International Conference on Robotics and Automation，2011：4638-4643.

[4]WOLF S，HIRZINGER G.A new variable stiffness design：Matching requirements of the next robot generation[C].In⁃ternational Conference on Robotics and Automation，2008：1741-1746.

[5]WOLF S，EIBERGER O，HIRZINGER G.The DLR FSJ：Energy based Design of a Variable Stiffness joint[C]//Inter⁃national Conference on Robotics and Automation，2011：5082-5089.

[6]TONIETTIG，SCHIAVIR，BICCHIA.Design and Control of a Variable Stiffness Actuator for Safe and Fast Physical Human/Robot Interaction[C]//International Conference on Robotics and Automation，2005：526-531.

[7]VAN H R，VANDERBORGHT B，VAN DAMME M，etal.MACCEPA：the Mechanically Adjustable Compliance and Controllable Equilibrium Position Actuator for'Controlled Passive Walking'Biped Veronica[C]//International Confer⁃ence on Robotics and Automation，2006：2195-2200.

[8]VANDERBORGHT B，TSAGARAKIS N G，SEMINI C，etal.MACCEPA 2.0：Adjustable Compliant Actuator with Stiffening Characteristic for Energy Efficient Hopping[C]//International Conference on Robotics and Automation，2009：544-549.

[9]BYEONG-SANG K，JAE-BOK S.Hybrid Dual Actuator Unit：a Design of a Variable Stiffness Actuator based on an Adjustable Moment Arm Mechanism[C]//International Con⁃ference on Robotics and Automation，2010：1655-1660.

[10]刘鸿文.材料力学-II[M].北京：高等教育出版社，2004.为弹性模块，从而实现具有可变刚度特性的关节驱动系统。笔者通过分析平面扭簧的刚度特性，给出了其表达式，除偏转角度与预紧量以外，其余参数均与其自身结构有关，这样就为进一步对平面扭簧参数的优化以提高关节驱动系统整体性能提供了理论依据；分析结果表明，本研究所用平面扭簧偏转角度约为7 °，刚度变化范围大，可满足机器人关节刚度需求。