基于机器视觉的葡萄树枝骨架提取算法研究*

贾挺猛，荀 一，鲍官军，董 茂，杨庆华

（浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，浙江 杭州 310014）

0 引 言

在葡萄生产作业中，为了提高果实品质，增加产量，果农需要对葡萄树进行整枝修剪。葡萄树修剪作业劳动强度较大，而目前机械化水平非常低，果农迫切需要高效省力的设备［1］，将他们从繁重的手工劳动中解救出来。因此，开展剪枝机器人的研究具有重要的实用价值［2］。

将机器视觉技术应用于工程中可以实现农业生产与管理的自动化和智能化。鉴于葡萄树枝上的各个芽粗细不均匀、形状不规则，直接从形态上检测并确定芽点位置具有一定的难度。

本研究采用机器视觉技术识别葡萄树枝干并提取葡萄树枝骨架，作为进一步确立葡萄树的芽点以及剪枝点的基础［3］。树枝骨架提取的优劣直接影响葡萄树枝芽点的识别。

1 葡萄树枝图像采集

实验研究的对象是葡萄冬剪之前的树枝，品种采用我国栽种面积最广的巨峰葡萄树，实验样本取自于杭州市萧山区海棠葡萄园，样本采用Y型种植方式，树龄为3年。

本研究以室内白色墙为背景采集葡萄树枝图像，在主动光源下，通过CCD工业摄像机采集巨峰葡萄树图像。

2 葡萄树枝图像预处理

本研究采集到的图像是24位的彩色图像。为了减少图像数据计算量，笔者将彩色图像中的3种基本颜色分量的亮度作为3个灰度图像的灰度值，输出R、G、B3个分量的直方图，对目标图像树枝和背景图像的灰度值分布情况进行了对比分析，发现B分量图中目标图像树枝的灰度值较为集中，与背景图像的灰度值区分最明显，相对较适合提取树枝对象。

因此，本研究选用B分量图作为后续处理图像，葡萄树B分量图像如图1所示。

图1 葡萄树B分量图像

本研究根据图像中背景与目标像素灰度值的分布特点，采用领域加权平均去除图像中的污点和部分背影，选择合理的阈值进行图像分割，即可消除铁丝、阴影，并得到葡萄树枝二值图像。鉴于葡萄树枝二值图像提取不够完整，且出现空洞的现象，本研究运用闭运算，以填充空白区域。

经过以上处理后得到的葡萄树二值图像如图2所示。

图2 预处理后的葡萄树二值图像

3 葡萄树骨架提取

骨架的提取一般采用细化算法。已有的细化算法按迭代方式不同分为串行算法和并行算法。串行细化即是一边检测满足细化条件的点一边删除细化点，并行细化即是检测细化点的时候不进行点的删除只进行标记，而在检测完整幅图像后一次性去除要细化的点。由于串行细化算法的处理结果依赖于对像素处理的先后顺序，像素点的消除或保留不可预测；而并行细化算法在对图像进行细化时利用相同的条件同时检测所有像素点，其结果具有各向同性，因此从算法原理上看，并行方法优于串行方法［4］。目前应用比较广泛的并行细化算法有形态学细化算法［5］、Zhang细化算法［6］、Rosenfeld细化算法［7］。

3.1 形态学细化算法

数学形态学的基本运算有膨胀（或扩张）、腐蚀（或侵蚀）、开启和闭合4种。研究者通过基本运算还可推导和组合成各种数学形态学实用算法，进行图像形状和结构的分析及处理。击中/击不中变换是在腐蚀和膨胀的基础上提出的［8-9］。

本研究设A为目标图像，Ac为图像A的补集，结构元素S由不相交的两部分S1和S2组成，即S=S1∪S2，且S1∩S2= ∅ ，而S2v表示关于原点的反射集，则A被S击中的结果可表示为:

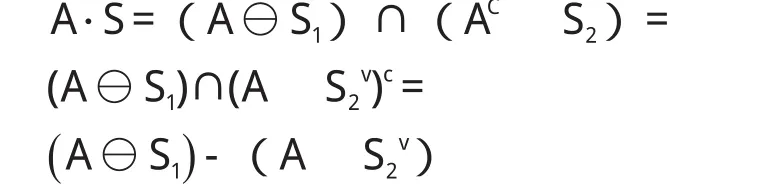
由此可看出，A被S的击中结果可以理解为A中具有S1几何特征的部分除去A中具有S2几何特征的部分的差集，另外，击中/击不中运算也可以利用腐蚀和膨胀操作来实现。借助于腐蚀、膨胀两个基本运算来理解，A被S击中的结果相当于A被S1腐蚀的结果与A被S2的反射集S2v膨胀的结果之差。

击中/击不中运算可以用于保持拓扑结构的形状细化，以及形状的识别和定位。

数学形态学细化算法便是一种常见的使用击中/击不中变换的形态学算法。其基本思想是:在给定系列具有一定形状的结构元素后，顺序循环地删除满足击中变换的像素，具体描述如下:

对于结构元素对S=(B,C)，利用S细化A定义为:AS=A-(A·S)。即AS为在A中去掉A被S击中的结果。

更一般地，利用结构元素对序列S1，S2，…SK，迭代地产生输出序列:

换而言之，该过程是先用S1细化一遍，然后再用S2对前面结果细化一遍，如此继续直到用SK细化一遍，整个过程可再重复，直到没有变化产生为止。假设输入集合是有限的，最终得到一个细化的对象。结构对的选择仅受结构元素不相交的限制。事实上，每一个Si都可以是相同的结构对，即在不断重复的迭代细化过程中使用同一个结构对。如果在对图像细化的过程中，仅使用一个结构对，则细化是有方向的。如果循环使用8个方向的结构元素对，则细化可以以更对称的方式完成。

3.2 Zhang细化算法

Zhang快速并行细化算法是Zhang在1984年提出的。设已知目标点标记为1，背景点标记为0。定义边界点是本身标记为1而其8连通邻域中至少有1个点标记为0的点。

（1）考虑以边界点为中心的8邻域，设P1为中心点，对其邻域的8个点逆时针绕中心点分别标记为P2，P3，…，P9，其中P2位于P1的上方。如果P1=1（即黑色像素），若同时满足下面4个条件:

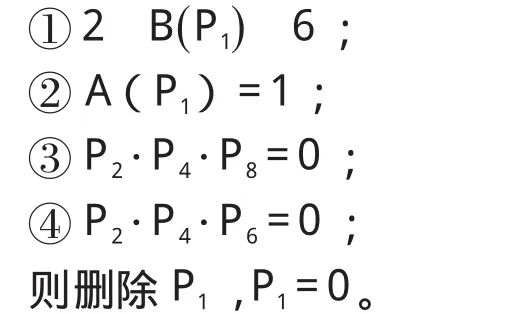
其中，B(P1)是P1的非零领点的个数；A(P1)是以P2，P3，…，P9为序时这些点的值从0～1变化的次数。对所有边界点检验完毕后，将所有标记点去除。

（2）第2步与第1步类似，仅需将条件③和④替换为条件⑤和⑥。如果P1=1（即黑色像素），同时满足下面4个条件:

同样对所有边界点都检验完毕后，将所有标记点去除。

（3）以上两步操作构成一次迭代，多次迭代运算直至没有点再满足条件，算法结束，这时剩下的点组成区域的骨架［10］。

3.3 Rosenfeld细化算法

Rosenfeld细化算法属于并行细化算法，实际上是基于模板匹配的一种算法。设已知目标点标记为1，背景点标记为0。定义边界点是本身标记为1而其8连通邻域中至少有1个点标记为0的点。目标像素3×3领域以P1为中心点，对其邻域的8个点逆时针绕中心点分别标记为P2，P3，…，P9，其中P2位于P1的上方。Rosenfeld细化实质上需要对目标像素点进行两步模板匹配，算法的具体步骤如下:

步骤一:首先用如图3所示的模板一中4个模板进行匹配。如果模板匹配成功，表明目标点P1位于边界位置，那么进行步骤二的8个模板匹配；如果模板匹配失败则跳过P1点，进行下一个像素的检验。图中4个模板中X代表0或1。

图3 模板一

步骤二:在步骤一中4个模板匹配成功之后，就进行如图4所示的模板二中的8个模板匹配。如果8个模板中有任何一个匹配，表面P1属于单像素连接点，删除P1会破坏目标图像的连通性；如果8个模板都没有匹配成功，则P1点删除，即由1变为0。然后进入下一像素的检验。以下8个模板中，X代表为0或1；3个Y中至少有一个Y为1，即Y+Y+Y 1。

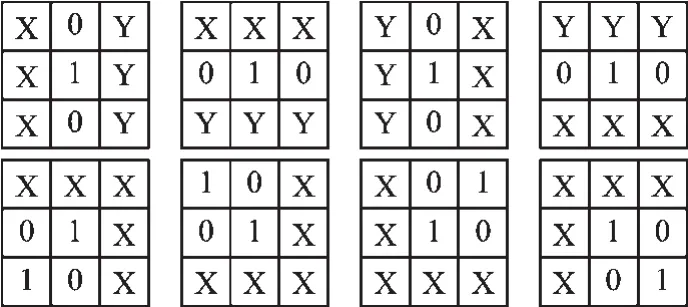
图4 模板二

步骤三:对于图像中所有像素进行步骤一、二中的模板匹配，迭代运算直至整幅图像没有可以再删除的像素点，最终得到的图像即为骨架。

4 实验与分析

本研究使用VC++6.0编程工具，分别将以上3种经典细化算法应用于葡萄树枝的骨架提取，骨架图像如图5～7所示。

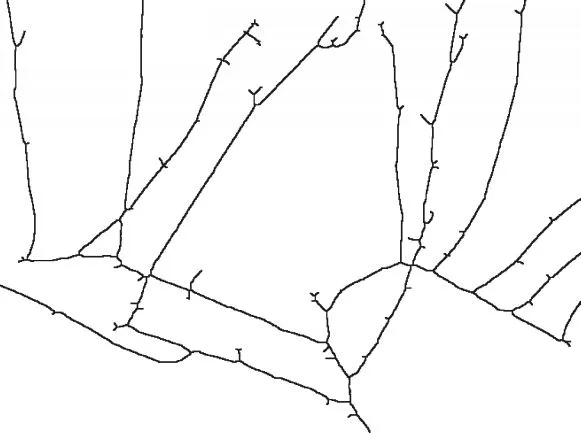
图5 形态学细化

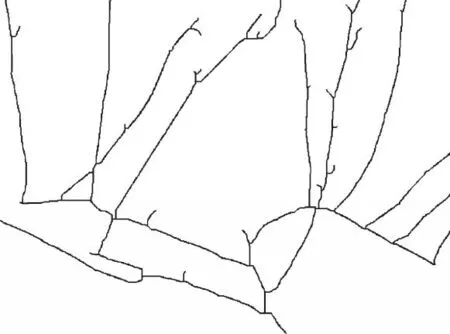
图6 Zhang细化算法

图7 Rosenfeld细化

合理的骨架提取算法应该达到以下要求:①骨架图像必须保持原图像的连通性；②骨架图像应尽可能是原图像的中心线；③骨架图像应尽可能细，最好单像素。

本研究依据合理骨架的基本要求，对3种骨架提取的效果进行对比分析。

树枝在某些局部位置，因其树皮粗糙、枝干粗细不均匀，形状不规则等问题，树枝边缘难免出现一些细微毛刺。局部毛刺对比如图8所示，从图8中可以看出，3种细化算法中，形态学细化算法对于此类毛刺干扰较为敏感，细化后容易出现冗余的细小分支。

局部连通性对比如图9所示，图9中Zhang细化图像在树枝的分枝处易发生形变、错位，改变了原图像的连通性。而形态学细化和Rosenfeld细化较好地维持了图像的连通性。

局部中心位置对比如图10所示，图10中Zhang细化所得局部图像中，中间连接部分枝干明显发生移位，偏离了原图中对应的中心线位置。而形态学细化和Rosenfeld细化相对较接近中心线位置。

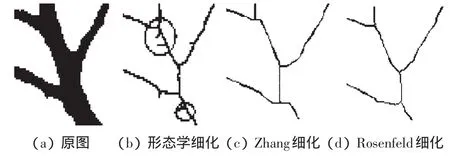
图8 局部毛刺对比

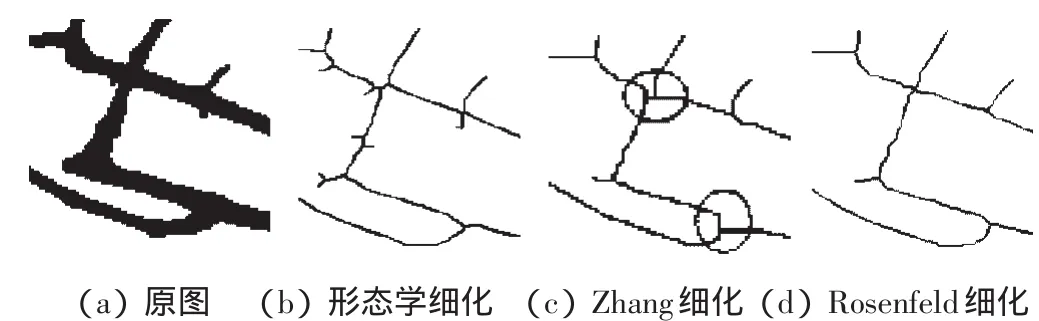
图9 局部连通性对比

图10 局部中心位置对比

由于目标图像树枝像素占总图像像素比例不高，计算量不大，3种细化算法均能快速取得计算结果，满足实际应用要求。

综合以上因素，Rosenfeld细化算法满足骨架提取的3个基本要求，所提取的葡萄树枝骨架图像较为理想。

5 结束语

本研究介绍了葡萄树枝实验图像的采集环境和方法，通过滤波、阈值分割等预处理提取了葡萄树枝二值图像。笔者分别采用图像形态学细化算法、Zhang细化算法以及Rosenfeld细化算法对葡萄树枝进行骨架提取，并分析比较了3种算法的处理效果。形态学细化算法对于树枝边缘毛刺较为敏感，容易产生冗余小分支；Zhang细化在树枝的分枝处的连通性及中心性较差。

实验结果表明，Rosenfeld细化算法最为理想，更适用于提取葡萄树枝图像的骨架，为进一步检测葡萄树枝的芽点奠定了基础。

（References）:

［1］胡 伟.葡萄生产机械化作业环节及要求［J］.农业机械，2005（5）:82-83.

［2］GAO Ming，LU Tien-fu.Image Processing and Analysis for Autonomous Grapevine Pruning［C］//Proceedings of the 2006 IEEE.Luoyang:［s.n.］，2006:922-927.

［3］LEE M F.An Intelligent Computer Vision Control and Tar⁃get Tracking System Design of an Agricultural Grapevine Pruning Robot［D］.Ithaca:Cornell University，1996.

［4］王家隆，郭成安.一种改进的图像模板细化算法［J］.中国图象图形学报，2004，9（3）:297-301.

［5］江 萍，徐晓冰，方 敏.基于形态学骨架提取算法的研究及其实现［J］.计算机应用，2003，23（S1）:297-137.

［6］ZHANG T Y，SUEN C Y.A fast parallel algorithm for thin⁃ning digital patterns［J］.Communications of the ACM，1984，27（3）:236-239.

［7］PAVLIDIS T.Algorithms for Graphics and Image Process⁃ing［M］.Washington DC:Rockville Computer Science Press，1982.

［8］左 飞，万晋森，刘 航.数字图像处理与实践:基于Visu⁃al C++开发［M］.北京:电子工业出版社，2011.

［9］崔 屹.图象处理与分析-数学形态学方法及应用［M］.北京:科学出版社，2000.

［10］吴选忠.Zhang快速并行细化算法的扩展［J］.福建工程学院学报，2006，4（1）:89-92.