转动薄壁圆柱壳行波振动响应分析

孙述鹏，曹登庆，初世明

（哈尔滨工业大学航天学院，黑龙江 哈尔滨 150001）

引 言

转动薄壁圆柱壳在诸多工程机械中应用广泛，如高速离心机、航空发动机高速转动鼓筒等。转动所带来的科氏力、离心惯性力及环向初应力，使得转动薄壁圆柱壳具有不同于静态圆柱壳的动力学特性。具体说来，一方面，离心惯性力使壳体结构产生环向初应力，导致壳体刚度增加，从而使转动薄壁圆柱壳频率随转速的升高而增加；另一方面，受转动速度矢量与变形速度矢量不一致而导致的科氏力的影响，转动薄壁圆柱壳频率随转速的变化发生分岔，产生不同频率的前、后行波，区别于静态圆柱壳频率所对应的驻波（振型）。转动薄壁圆柱壳这种行波振动的特点，使得传统的求解静态圆柱壳振动响应的方法不再适用。因此，对转动薄壁圆柱壳行波振动响应的研究，具有重要的理论意义和应用价值。

国内外众多学者通过解析、数值、实验等手段对转动薄壁圆柱壳的自由振动问题进行了大量的研究工作［1～12］，比较之下，对激振力作用下转动薄壁圆柱壳行波振动响应的研究则相对较少［13～16］。在为数不多的行波振动响应研究中，以Huang的工作最具代表性［13～15］。Huang将两端简支圆柱壳行波模态（travelling mode）代入基于Love－Timoshenko壳体理论的转动薄壁圆柱壳的振动微分方程中，并利用三角函数的正交性将方程离散为常微分方程组，通过数值求解常微分方程组，进而采用类似模态叠加的方法求得响应。基于此思路，Huang着重分析和探讨了科氏力对两端简支转动圆柱壳强迫振动的影响以及简谐移动载荷作用下的转动薄壁圆柱壳体的共振现象。需要指出的是，Huang的结果，均针对两端简支边界条件的转动柱壳，而对其他类型的边界条件并没有提及。两端简支约束的圆柱壳的振型可以解析地表达为三角函数组合的形式，而对于其他类型边界条件下圆柱壳的振型，解析表达式的获取则是困难的，因此有必要发展一种适用于求解各种类型边界约束的转动薄壁圆柱壳行波振动响应的方法。国内也有部分学者在转动薄壁圆柱壳振动响应的求解方面做了一些工作。如李健等应用Donnell壳体理论［16］，采用复分析的方法研究了转动薄壁悬臂圆柱壳在法向激励作用下的行波振动。因作者仅通过在静态薄壁圆柱壳上施加反向转动的激励来处理转动柱壳受迫振动问题，因此转动所带来的离心惯性力、科氏力等的影响未能在模型中反映出来，并且作者采用的Donnell简化壳体理论尽管形式简单，但因其主要考虑法向弯曲变形，忽略了平面内两个方向的惯性力，不能准确反映3个方向运动的耦合，且对环向波数较小的模态，频率计算并不准确。

本文考虑由转动引起的科氏力、离心惯性力及环向初应力影响，利用Hamilton原理，建立了基于Sanders壳体理论的转动薄壁圆柱壳振动微分方程［17］。选取满足相应边界条件的轴向梁函数来逼近各类边界条件下的圆柱壳轴向振型分布［18］。进而采用Galerkin方法，对振动微分方程进行离散，得到6自由度陀螺转子系统的动力学方程。然后，通过叠加各行波模态的响应，得到了任意典型边界条件下转动薄壁圆柱壳行波振动响应一般解的形式。最后，分别针对静坐标系下横向简谐力和恒力作用下的两端固支转动薄壁圆柱壳的行波振动响应，给出了相应算例，并对结果进行了简要分析。

1 基于Sanders壳体理论的转动薄壁圆柱壳振动微分方程

考虑长L、厚H、半径为R，并以角速度Ω绕中轴转动的各向同性薄壁圆柱壳，该圆柱壳的密度、弹性模量、泊松比分别为ρ，E，μ。如图1所示，正交曲线坐标系（x，θ，z）为建立在壳体中曲面上的动坐标系。相对于该坐标系，壳体中曲面上点的轴向、切向、法向的变形位移分别为u，v，w。在壳体中面微元上，x，θ，z三个方向的单位面积外载荷分量分别为qx，qθ，qz。

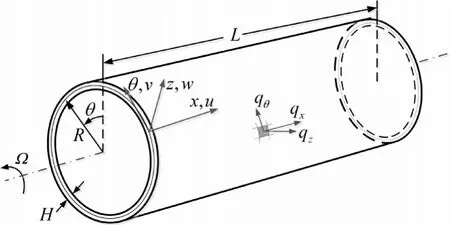
图1 载荷作用下的转动薄壁圆柱壳模型图Fig．1 Sketch of the geometrical relations of a thin rotating cylindrical shell

转动薄壁圆柱壳的动能可表示为

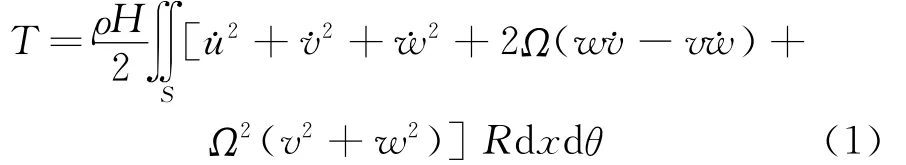
由环向初应力所引起的初应变能为［11］

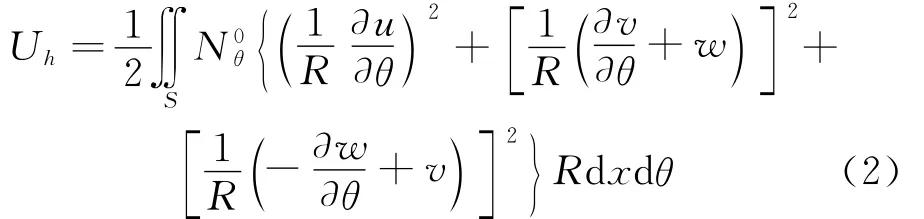
式中＝ρHΩ2R2为离心惯性力导致的环向初应力。

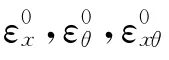
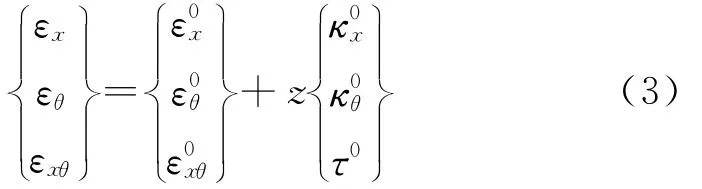
其中，基于Sanders壳体理论的薄壁圆柱壳中曲面的薄膜应变分量与弯曲应变（曲率变化）分量可分别表示为

考虑各向同性薄壁圆柱壳，有应力－应变关系如下

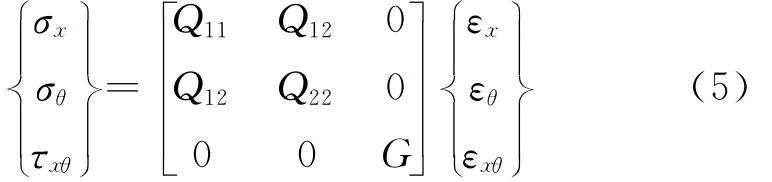
其中

薄壁圆柱壳应变能可表示为

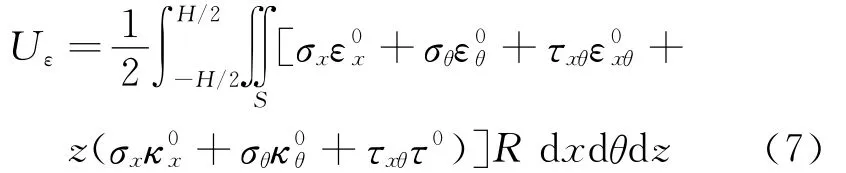
综合考虑式（2）及（7），可得转动薄壁圆柱壳总的应变能

面载荷所做虚功可表示为

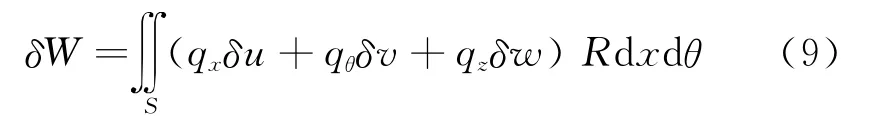
由哈密顿原理，可导出基于Sanders壳体理论的转动薄壁圆柱壳振动微分方程如下

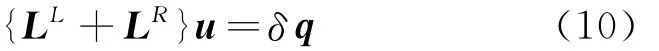
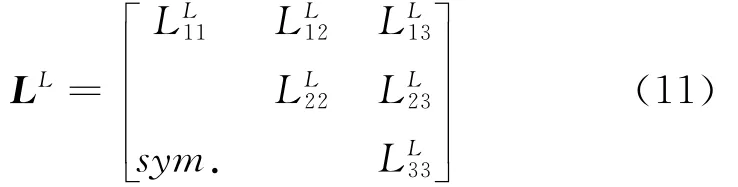
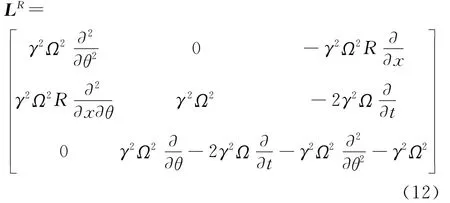
实际工程系统不可避免存在阻尼因素，受阻尼影响，系统瞬态响应将衰减，进而剩余工程中关心的稳态响应。通常情况下，阻尼是由试验测定的，这里假设阻尼为等效粘性阻尼，比例系数为ιmn，并在建立的振动方程中引入阻尼项。振动控制方程（10）可改写为如下形式

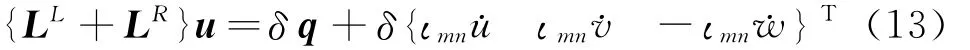
2 转动薄壁圆柱壳行波振动响应一般解

对转动薄壁圆柱壳体自由振动特性的研究表明［19］，转动引起的离心惯性力使壳体产生周向应力，导致壳体刚度增加，从而使得转动薄壁圆柱壳较静态圆柱壳频率有所增加；同时，受转动薄壁圆柱壳变形速度矢量与转动速度矢量方向不同所引起的科氏力影响，转动薄壁圆柱壳频率随转速变化发生分岔，产生频率不同的前、后行波。此时的模态已不是通常意义下的振型（驻波），而是与时间有关的行波。基于此，将转动薄壁圆柱壳行波振动解的一般形式设为如下形式：

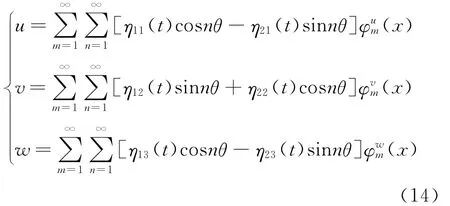
考虑到除两端简支约束薄壁圆柱壳外，具有其他边界条件的圆柱壳轴向振型分布很难用解析式表示出来，这里利用圆柱壳振型的轴向分布接近于相应边界条件梁振型函数的特性，采用梁函数来逼近圆柱壳轴向振型函数。一般可设3个方向的振型分布有如下形式［18］

式中ψ（x）为相应边界条件下连续梁的振型函数，一般形式如下

系数ci（i＝1，…，4）由边界条件决定。为后面算例中分析方便，这里给出两端固支连续梁的振型函数，其他边界条件的梁的振型函数可以参考振动理论的相关内容。

固支－固支边界条件下，梁的振型函数为［20］

其中

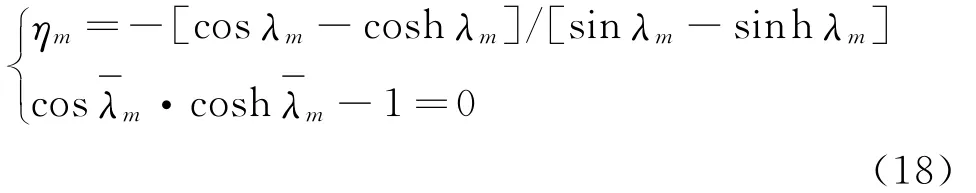
将解的形式（14）代入转动薄壁圆柱壳振动微分方程（13），并采用Galerkin方法进行离散，对每个m，n组合的模态可得到一个6自由度系统动力学方程，写成矩阵形式有

对方程（19）进行数值积分，可得每个m，n组合的模态所对应的广义坐标的时间历程。理论上讲，将各个m，n组合的模态所对应的广义坐标的时间历程，运用式（14）进行叠加，即可得出转动薄壁圆柱壳上各点的行波振动响应。

值得注意的是，环向波数n＝0时，转动圆柱壳的各阶模态均表现为驻波的形式，而考虑到本文主要探讨的是转动圆柱壳的行波振动响应的求解方法，因此在式（14）中没有考虑n＝0这一特殊模态。

3 数值结果与讨论

根据前面给出的方法，针对具有两端固支约束的转动薄壁圆柱壳模型，进行了计算和分析，算例所用几何参数及材料常数列于表1。考虑到壳体的面外弯曲振动是对壳体动力学特性起主导作用的振动形式，故这里只分析对应于弯曲振动的行波频率特性，和法向的位移响应w。

表1 几何参数及材料常数Tab．1 Geometric parameter and material property

3．1 行波振动频率特性与模型验证

忽略阻尼，则对每个m，n组合的模态所对应的6自由度系统动力学方程（19）可退化为陀螺转子系统动力学方程的形式

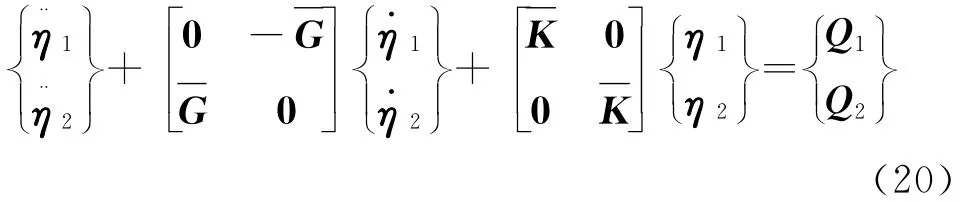
因此，求解转动薄壁圆柱壳行波频率的问题，就转化为求解陀螺系统特征值问题。Meirovitch给出了求解此类特征值问题的方法［21］。需要指出，对于每个m，n组合的模态，有6个频率值，其中频率最低的两个对应于w方向弯曲振动为主的行波频率。

为验证离散模型的正确性，本文将所求得的行波频率与由文献［6］中的解析表达式所得结果进行了比较，两者结果吻合，如表2所示。

图2所示为转速6 000r／min，轴向振型阶数m＝1情况下，动坐标下中行波频率随环向波数的变化曲线。动坐标系下，后行波频率大于前行波频率，且前、后行波频率随环向波数的增加均呈现先减小后增加的趋势，并在环向波数大于9时逐渐重合。图3所示为轴向振型阶数m＝1，环向波数n＝3时，动坐标系中行波频率随转速的变化曲线。如图3所示，转速为零时，前后行波频率值一致，产生的是驻波，即传统意义的振型。随着转速的增加，频率发生分岔，产生频率不同的前、后行波。前行波频率随转速升高先有微弱的减小趋势，继而随转速的升高而增加。而后行波频率随转速的变化，则一直呈现单调增加的趋势。

图2 行波频率与环向波数的关系曲线Fig．2 Variation of the frequency parameter with respect to the circumferential wave number

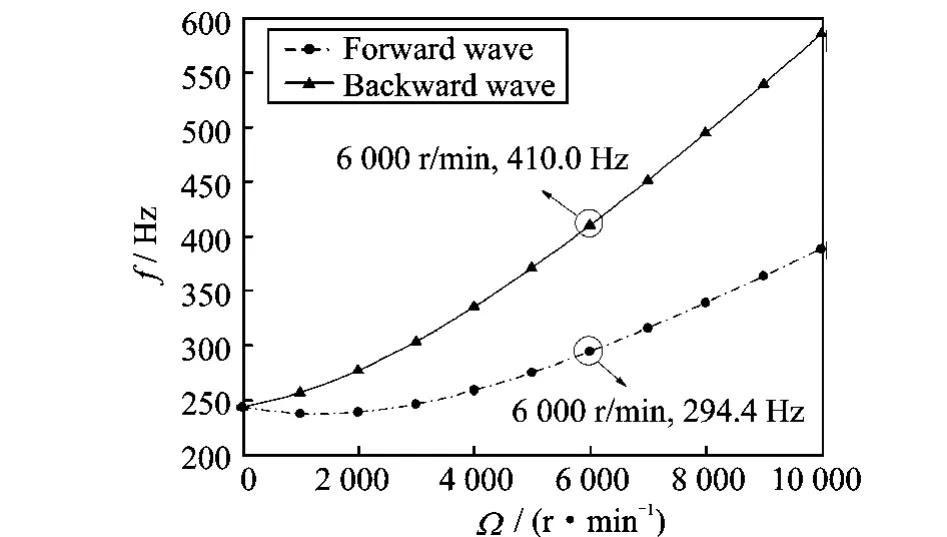
图3 行波频率随转速变化曲线Fig．3 Variation of the frequency parameter with respect to rotating speed

3．2 静坐标系中横向简谐力作用下的两端固支转动薄壁圆柱壳的行波振动响应

受静坐标下幅值为F，频率为的横向简谐力激励的转动薄壁圆柱壳，其所受单位面积外载荷分量可表示为

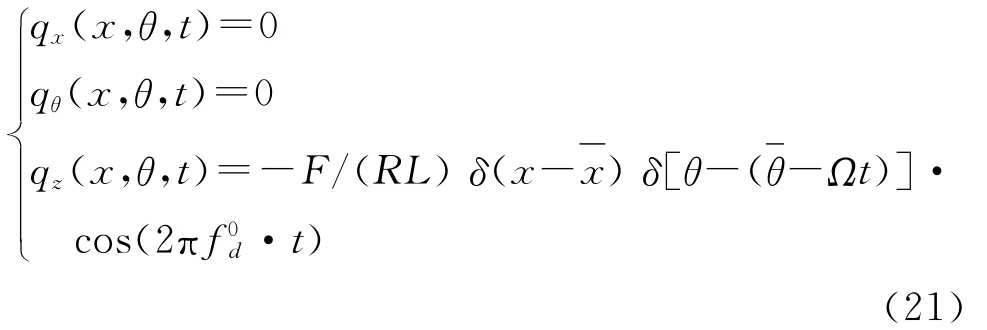
为计算和分析方便起见，这里仅取m＝1，n＝3所对应的行波模态，并根据式（14）进行叠加。

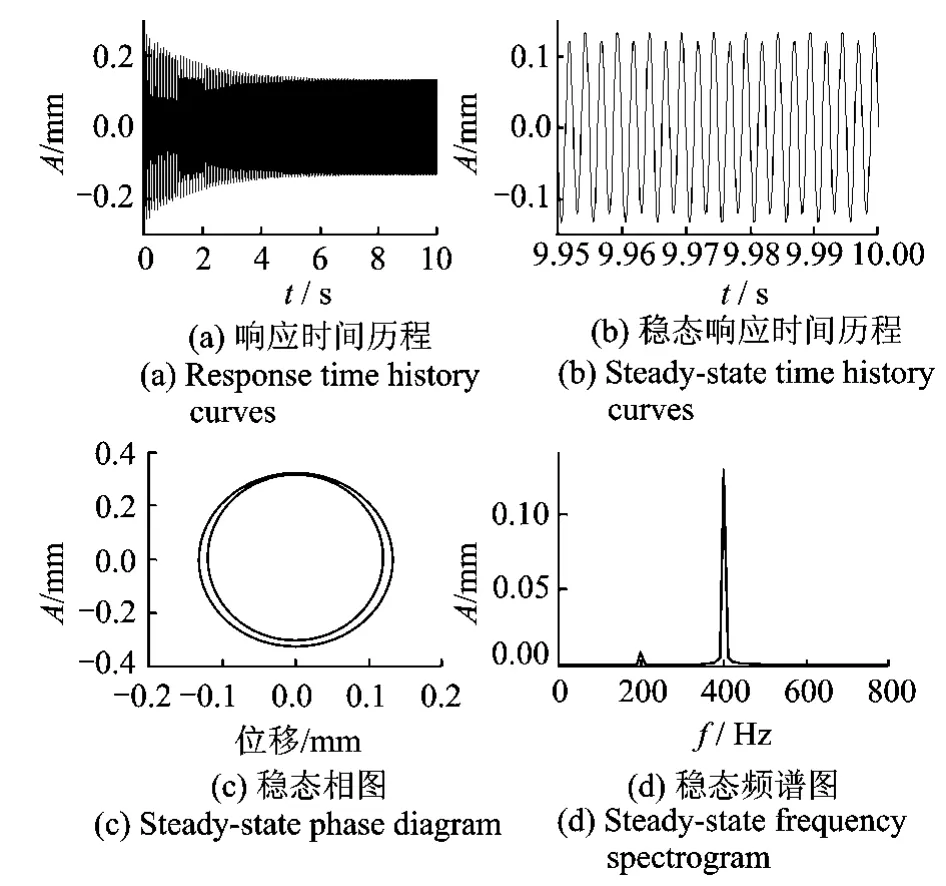
图4 静坐标中横向简谐力作用下（m＝1，n＝3）组合行波模态的响应Fig．4 Response of（m＝1，n＝3）travelling mode for a rotating cylindrical shell under transverse harmonic loads in the stationary coordinate

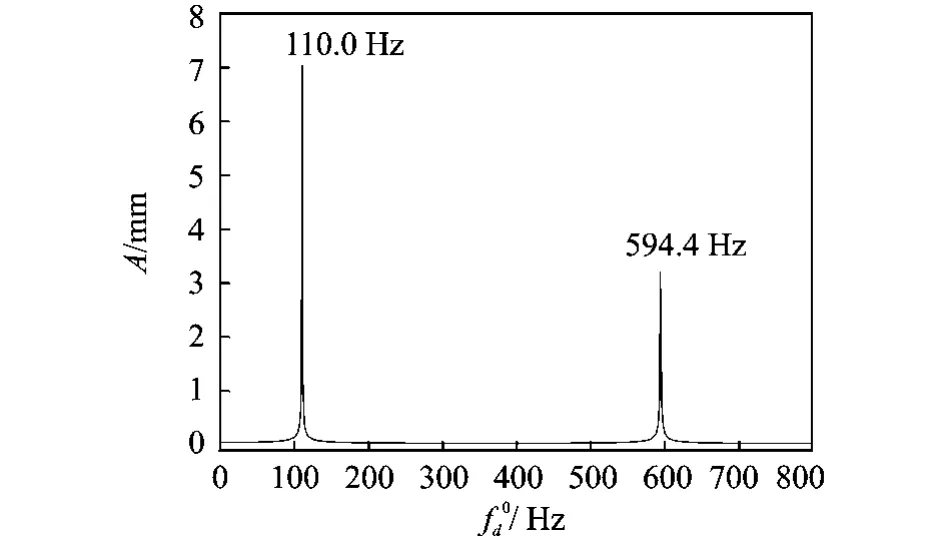
图5 静坐标系中横向简谐力作用下（m＝1，n＝3）组合行波模态响应的幅频曲线Fig．5 Amplitude－frequency curve of（m＝1，n＝3）travelling mode for a rotating cylindrical shell under transverse harmonic loads in the stationary coordinate

综合上面的分析可知，一般地，当静坐标系下横向简谐力的频率满足如下条件时，会发生行波共振，

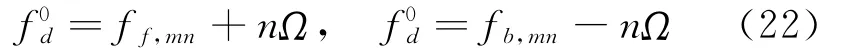
具有转动薄壁圆柱壳结构的实际工程系统，在工作时应尽量避开这些共振点。

3．3 静坐标系中法向恒力作用下两端固支转动薄壁圆柱壳的行波振动响应

令＝0，由式（21）可得，受静坐标下幅值为F的法向恒力作用的转动薄壁圆柱壳，其所受单位面积外载荷分量的表达式

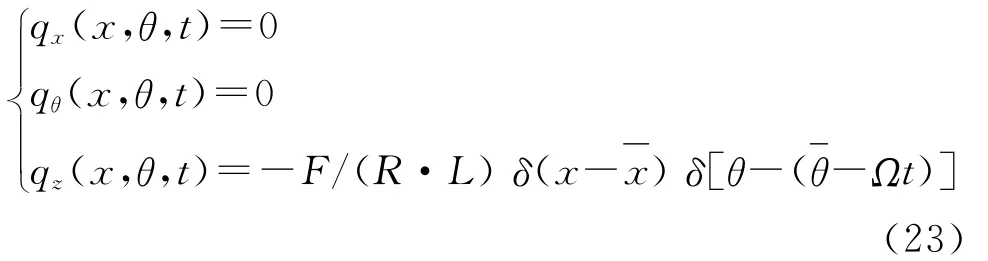
若（x＊，θ＊）表示初始时刻动坐标系中转动薄壁圆柱壳上一点P，此时该点位于静坐标下的空间点P0，两点重合。t时刻后，与静坐标下的空间点P0重合的转动薄壁圆柱壳上点的坐标则可表示为（x＊，θ＊－Ωt）。由式（14），相应点的位移响应为

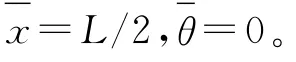
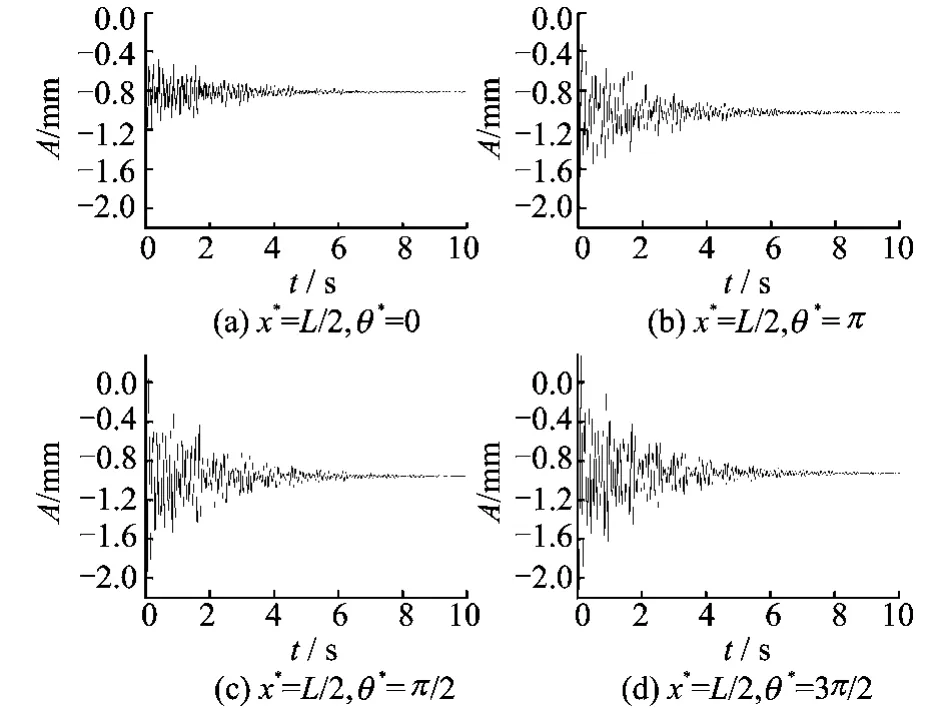
图6 与静坐标下空间点对应的转动薄壁圆柱壳上相应点的响应Fig．6 Response of one point on a rotating cylindrical shell in stationary coordinate

如图6所示，4个空间点所对应的转动薄壁圆柱壳上点的响应随时间变化逐渐收敛。即，静坐标系下法向恒力作用下的两端固支转动薄壁圆柱壳，其形变形状在达到稳态后不随时间而改变，如图7所示。从波动的观点讲，两端固支转动薄壁圆柱壳，受静坐标系下法向恒力作用，产生了静坐标系下的驻波。受此影响，当形变导致的应力水平超过材料破坏极限，可能产生破坏，此外也可能会给转动薄壁圆柱壳带来疲劳加速等问题，这些都是值得进一步研究的课题。

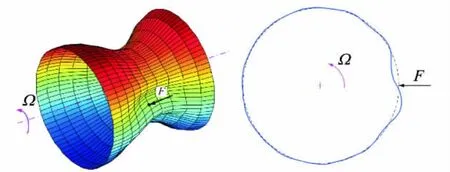
图7 静坐标系下法向恒力作用下的两端固支转动薄壁圆柱壳的形变Fig．7 Deformation of a rotating cylindrical shell under point force

4 结 论

本文考虑由转动引起的科氏力、离心惯性力及环向初应力影响，利用Hamilton原理，建立了基于Sanders壳体理论的转动薄壁圆柱壳振动微分方程，提出了一种适用于求解各种边界约束的转动薄壁圆柱壳行波振动响应的方法。基于此方法，分别针对静坐标系下横向简谐力和恒力作用下的两端固支转动薄壁圆柱壳的行波振动响应进行了求解和分析。得到以下结论：

（1）通过选取满足相应边界条件的轴向梁函数来逼近各类边界条件下的圆柱壳轴向振型分布，可以克服除简支以外的各类边界条件下圆柱壳振型的解析表达式不易获取的困难。在此基础上发展的方法，适用于求解各种类型边界约束的转动薄壁圆柱壳行波振动响应。

（2）两端固支转动薄壁圆柱壳，随着转速的增加，其频率发生分岔，产生频率不同的前、后行波。前行波频率随转速升高先有微弱的减小趋势，继而随转速的升高而增加。而后行波频率随转速的变化，则一直呈现单调增加的趋势。

（3）当静坐标系下横向简谐力的频率满足时，两端固支转动薄壁圆柱壳会发生行波共振，具有转动薄壁圆柱壳结构的实际工程系统，在工作时应尽量避开这些共振点。

（4）受静坐标系下法向恒力作用，两端固支转动薄壁圆柱壳会产生不随时间改变的形变，即静坐标系下的驻波。受此影响，当形变导致的应力水平超过材料破坏极限，可能产生破坏，此外也可能会给转动薄壁圆柱壳带来疲劳加速等问题，这些都是值得进一步研究的课题。

［1］ DiTaranto R A，Lessen M．Coriolis acceleration effect on the vibration of a rotating thin－walled circular cylinder［J］．ASME Journal of Applied Mechanics，1964，31：700—701．

［2］ Macke H J．Travelling－wave vibration of gas－turbine engine shells［J］．Journal of Engineering for Power，1966，88：179—187．

［3］ Srinivasan A V，Lauterbach G F．Travelling waves in rotating cylindrical shells［J］．Journal of Engineering for Industry，1971，93：1 229—1 232．

［4］ Zohar A，Aboudi J．The free vibrations of a thin circular finite rotating cylinder［J］．International Journal of Mechanical Sciences，1973，15：269—278．

［5］ Chung H．Free vibration analysis of circular cylindrical shells［J］．Journal of Sound and Vibration，1981，74：331—350．

［6］ Endo M，Hatamura K，Sakata M，et al．Flexural vibration of a thin rotating ring ［J］．Journal of Sound and Vibration，1984，92：261—272．

［7］ Saito T，Endo M．Vibration of finite length，rotating cylindrical shells［J］．Journal of Sound and Vibration，1986，107：17—28．

［8］ Li Hua，Lam K Y．Frequency characteristics of a thin rotating cylindrical shell using the generalized differential quadrature method ［J］．International Journal of Mechanical Sciences，1998，40：443—459．

［9］ Guo Dan，Zheng Zhaochang，Chu Fulei．Vibration analysis of spinning cylindrical shells by finite element method［J］．International Journal of Solids and Structures，2002，39：725—739．

［10］Liew K M，Ng T Y，Zhao X，et al．Harmonic reproducing kernel particle method for free vibration analysis of rotating cylindrical shells［J］．Computer Methods in Applied Mechanics and Engineering，2002，191：4 141—4 157．

［11］洪杰，郭宝亭，朱梓根．高速转动壳体行波振动实验研究［J］．航空动力学报，1998，13：390—394．

Hong J，Guo B T，Zhu Z G．Experimental investigation on travelling wave vibration of high－speed rotating shell［J］．Journal of Aerospace Power，1998，13：390—394．

［12］曹航，朱梓根．转动壳体行波振动的有限元分析方法［J］．航空动力学报，2002，17：222—225．

Cao H，Zhu Z G．Traveling－wave vibration of rotating shells by finite element method［J］．2002，17：222—225．

［13］Huang S C，Soedel W．Effects of Coriolis acceleration on the forced vibration of rotating cylindrical shells［J］．Journal of Applied Mechanics，1988，55：231—233．

［14］Huang S C，Soedel W．On the forced vibration of simply supported rotating cylindrical shells［J］．Journal of Acoustical Society of America，1988，84：275—285．

［15］Huang S C，Hsu B S．Resonant phenomena of a rotating cylindrical shell subjected to a harmonic moving load［J］．Journal of Sound and Vibration，1990，136：215—228．

［16］李健，郭星辉，李永刚．薄壁圆柱壳旋转波动振动分析［J］．东北大学学报（自然科学版），2007，28：553—556．

Li J，Guo X H，Li Y G．Analysis of wavy vibration of rotating thin cylindrical shells［J］．Journal of Northeastern University（Natural Science），2007，28：553—556．

［17］曹志远．板壳振动理论［M］．北京：中国铁道出版社，1989．

Cao Z Y．Vibration of Shells and Plates［M］．Beijing：China Railway Publishing House，1989．

［18］Lam K Y，Loy C T．Influence of boundary conditions and fibre orientation on the natural frequencies of thin orthotropic laminated cylindrical shells［J］．Composite Structures，1995，31：21—30．

［19］晏砺堂，朱梓根，李其汉．高速旋转机械振动［M］．北京：国防工业出版社，1994．

Yan L T，Zhu Z G，Li Q H．Vibration of High Speed Rotating Machinery［M］．Beijing：National Defense Industry Press，1994．

［20］刘延柱，陈文良，陈立群．振动力学［M］．北京：高等教育出版社，1998．

Liu Y Z，Chen W L，Chen L Q．Mechanics of Vibration［M］．Beijing：Higher Education Press，1998．

［21］Meirovitch L．A new method of solution of the eigenvalue problem for gyroscopic systems［J］．American Institute of Aeronautics and Astronautics，1974，12：1 337—1 342．