非平稳随机过程功率谱密度估计的小波方法

孔 凡，李 杰，2

（1．同济大学土木工程学院，上海 200092；2．同济大学土木工程防灾国家重点实验室，上海 200092）

引 言

工程结构在役期间，会受到各种非平稳随机动力的作用，如地震、强风以及海浪等。其非平稳性不仅表现在依赖于时间的幅值上，而且其频谱特性也是随时间变化的［1］。由平稳随机过程经过确定性函数调制所得的非平稳过程并不能合理反映频域非平稳性质［2］。获取非平稳随机过程的时间－频率特性，成为描述随机动力激励、计算结构随机动力响应的重要一环。

最早的频率分析工具为Fourier变换：它在频域内分辨率可视为δ函数，没有时间分辨率［3，4］，或者精确地讲，其时间信息湮灭在相位信息之中［3］。为了改进Fourier变换的不足，人们提出了Gabor展 开／短 时 Fourier 变 换 （Short Time Fourier Transform，STFT）以及 Wigner－Ville分布（Wigner－Ville Distribution，WVD）方法［5～9］。这些方法虽然能体现非平稳过程的某些时间－频率特征，但它们都有各自的缺点和不足［4］。近30年来发展起来的小波分析［3，10～13］方法，因其具有良好的时－频分辨率、丰富的小波基以及逐渐完备的数学背景，使其在工程方面得到了广泛的应用。

在利用小波分析估计非平稳功率谱密度方面，Basu等人建立了小波变换系数的均方值与功率谱密度之间的关系［14～17］；Liang等人在文献［18］中使用了这一方法估计由非平稳过程谱表达方法合成的非平稳随机过程的功率谱密度。值得指出的是，Basu关系式只适用于频域内互不重叠的小波族［19］。Spanos等人发展了利用正交且频域内不重叠的谐和小波（Harmonic Wavelet，HW）以及广义谐和小波（Generalized Harmonic Wavelet，GHW）估计非平稳随机过程功率谱密度的方法（简称Spanos－Tratskas方 法）［10，20～26］。随 后，结 合 Wold－Cramer非平稳随机过程［27，28］，Spanos和Failla提出了适合一般非正交小波（简称为“一般小波”）估计非平稳随机过程演变功率谱密度的方法（简称Spanos－Failla方法）［29］；Huang等人把这种方法推广于多维随机过程以及强风的演变功率谱估计［19］；Chakraborty等人采用这种方法计算了大跨桥梁的随机非平稳响应［30］；基 于 Spanos－Failla方 法，Failla等 人 发 展 了非平稳随机过程小波谱的思想［31］，并且证明此方法能推广应用于一般非Cramer－Wold模型的非平稳随机过程。

本文首先证明，基于谐和小波和广义谐和小波估计随机过程功率谱密度的Spanos－Tratskas方法为Spanos－Failla方法的特殊情况；比较了文献［14～16］所提之修正的 Littlewood－Paley（Modified Littlewood－Paley，MLP）小波与GHW在估计非平稳随机过程EPSD方面的特点。研究表明，当使用Spanos－Failla方法估计功率谱密度时，小波尺度的选取、小波边缘效应以及非平稳过程调制函数的变化快慢均对功率谱的估计有较大影响。数值计算表明，补零延长（Zeros Padding）对于边缘效应有较好的消除作用。随后，在最近提出的局部平稳小波过程（Locally Stationary Wavelet process，LSW）的基础上［32，33］，提出了一种新的估计非平稳随机过程的方法，它不仅适用于正交小波，而且适用于一般非正交小波。有趣的是，本文建议方法不仅可与Spanos－Failla方法在形式上统一起来，而且广义谐和小波的应用，使二者退化为同一形式。简言之，本文从随机过程LSW模型的角度，证明了Spanos－Tratskas方法不仅适用于基于 Wold－Cramer模型的Priestley演变功率谱密度，而且可以估计任意非平稳随机过程的时变功率谱密度。这一点，与作者刚注意到的文献［31］有类似的结论：Failla从另一个角度证明了Failla－Spanos方法能适用于任意非平稳随机过程。为了验证所提之方法的有效性，文章最后给出了基于GHW且在考虑场地土与行波效应情况下的多维地震动互／自功率谱的数值算例。在确定性时程时－频谱分析方面，以汶川地震中离断层最近的绵竹清平波和Ⅲ类远场地的西安波为例，利用GHW对二者进行了时频谱分析，讨论了导致近场地和远场地时－频谱迥异的物理原因。

1 非平稳随机过程的EPSD估计

考虑形非平稳随机过程的Wold－Cramer模型

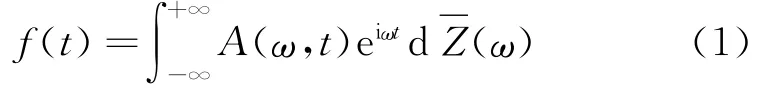
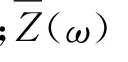
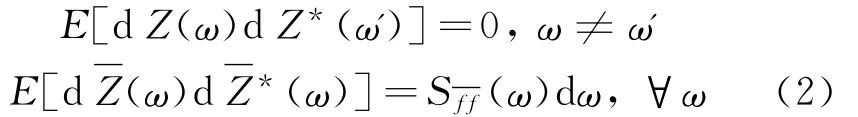
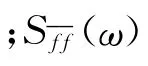
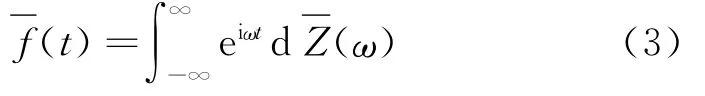
的双边功率谱密度。Priestley为此类非平稳随机过程定义了（双边）演变功率谱密度［28］

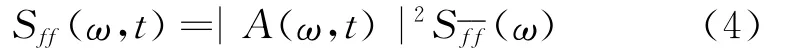
可以证明，非平稳随机过程f（t）的演变功率谱密度可以表达为

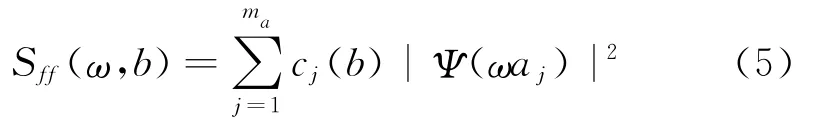
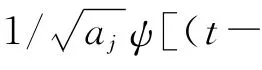
式中W（ar，b）为非平稳随机过程f（t）在尺度ar和时间b处的小波变换，且

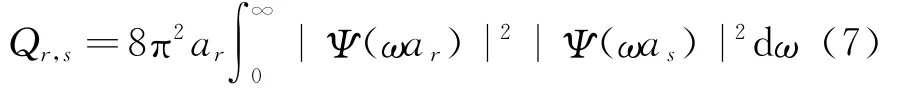
式（5）可视为非平稳随机过程小波谱估计值［31］：在特定时间点b处，随机过程的瞬时功率谱密度由各阶小波的Fourier变换之模的平方构造而成，cj（b）为瞬时各阶加权值。

另一方面，当使用正交且在频域内紧支无重叠的GHW估计功率谱时，Spanos等人给出了如下随机过程功率谱与其小波变换系数之间的关系式［23～26］

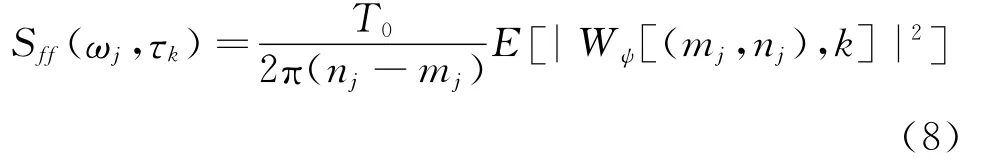
式中 （mj，nj）为GHW的尺度因子；k为其时间平移因子；Wψ［（mj，nj），k］为非平稳随机过程在相应尺度和时间点上的 GHW 变换且mjΔω＜ωj≤njΔω。

可证明当式（5）中一般小波退化为GHW时，与式（8）是统一的。事实上，当小波为GHW时，由于其在频域内的特殊性，仅依赖于小波形式的矩阵Q为对角阵，且

结合式（9）与式（6），易证基于 GHW 的 Spanos－Failla方法退化为如式（8）所示的Spanos－Tratskas方法。具体而言，由式（9）可知，频域内紧支且不重叠导致了矩阵Q的对角化，进而导致了系数cj（b）与小波变换均方值E［｜W（aj，b）｜2］具有正比关系。非平稳随机过程小波谱思想和GHW的引入，更清楚地表明了非平稳随机过程瞬时功率谱密度与各阶GHW的Fourier变换均方值之间的关系，如图1所示。显然，GHW对瞬时功率谱的估计类似于函数的分段常数插值。值得指出的是，类似于式（8），文献［14～16］利用MLP小波从不同的角度也得到了类似于Spanos－Tratskas方法的非平稳随机过程瞬时PSD与小波系数模的均方值之间的关系

图1 非平稳随机过程瞬时EPSD与其GHW估计Fig．1 Instantaneous PSDof non－stationary stochastic process and the GHW estimation

其中，K为与小波容许条件［11］以及离散格式相关的常数。

基于上述背景，有如下注记：

（1）MLP小波是一种正交二进小波（Dyadic Wavelet），为谐和小波的实部。因此，式（10）显然适用于MLP小波。而对于其他在频域内非紧支且重叠的小波，则宜使用Spanos－Failla方法估计演变功率谱。导致这种现象发生的原因为：其一，由于GHW或MLP小波在频域内的特别性，使其具有明确的尺度－频率关系，而其他在频域内非紧支且重叠的小波（简称为“其他小波”）没有明显的这种关系；其二，频域内一般小波在不同尺度处重叠部分的能量被重复计算，导致了利用其他小波和式（10）所估计的演变功率谱密度大于目标演变功率谱密度［19］。图2所示为不同尺度Morlet小波在频域内的表达，清楚地反映了这一点。

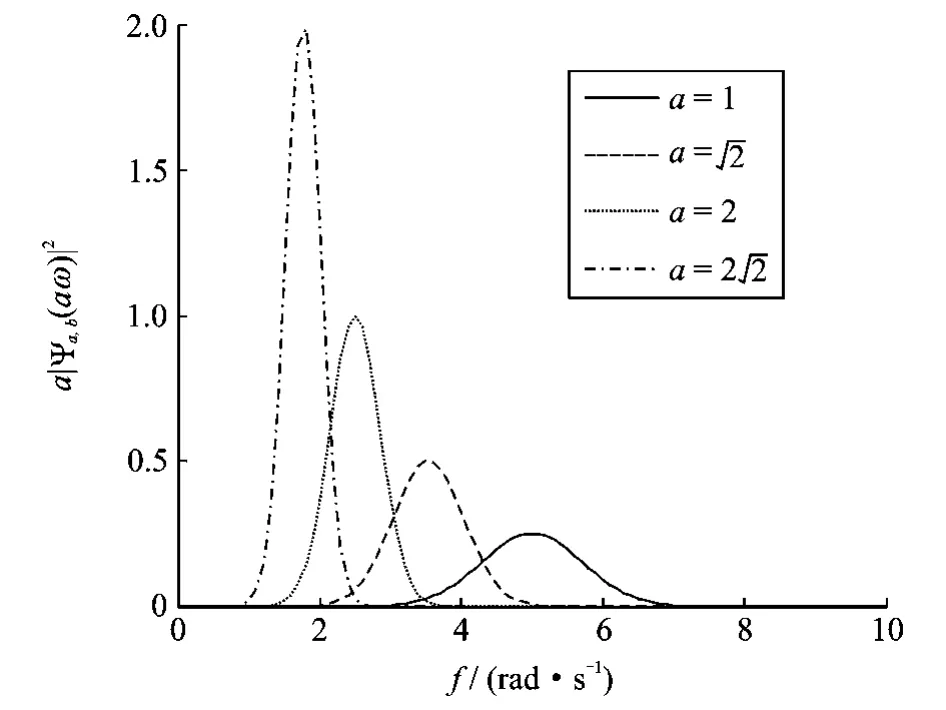
图2 不同尺度的小波在频域内的重叠Fig．2 Mean square value of Fourier transform of Morlet wavelets at different scales

（2）虽然利用实值的MLP小波能较好地估计单变量随机过程的演变自功率谱密度，却不能估计多变量随机过程的演变互功率谱密度。因此，对于多维／多变量非平稳随机过程演变互功率谱密度的估计，复值的GHW显然更具优势。除此之外，由于MLP小波是二进小波，不同尺度小波在频域内所占频宽依2的倍数增长。当随机过程的演变功率谱为慢变、宽频且峰值出现在低频处时，MLP小波尚能较好估计；如果演变功率谱在高频处出现快变峰值，MLP小波不能满足要求，如图3所示。因此，虽然文献［15，16］中所建议的MLP小波，限制了其母小波频宽，因此对于高频峰值的EPSD估计起到一定改进效果，但小波个数的增加却带来了额外的计算量。

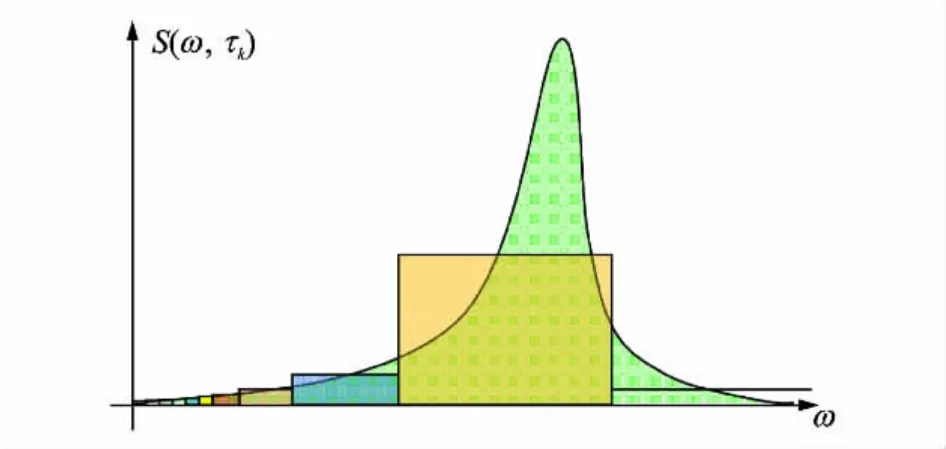
图3 L－P小波对高频峰值的瞬时功率谱的估计Fig．3 L－P wavelet based estimation of EPSD with a peak at high frequency

（3）在利用Spanos－Failla方法估计EPSD时，适当选择小波尺度至关重要。计算表明，尺度因子选择不当会导致低频处估计功率谱失真或估计功率谱异常波动。图4（a）所示为在不同尺度选择下，基于Morlet小波的一致调制非平稳随机过程的功率谱估计，调制前的平稳PSD选为Kanai－Tajimi谱。从图4（b）易见不同尺度下Morlet小波的频域峰值构成：由于不当的小波尺度选择，导致图4（b）中不同尺度小波的Fourier变换异常明显，从而不能较好地逼近目标演变功率谱。计算实践表明，小波尺度的选择决定了矩阵Q的条件数，而后者直接影响了功率谱估计的精确程度。

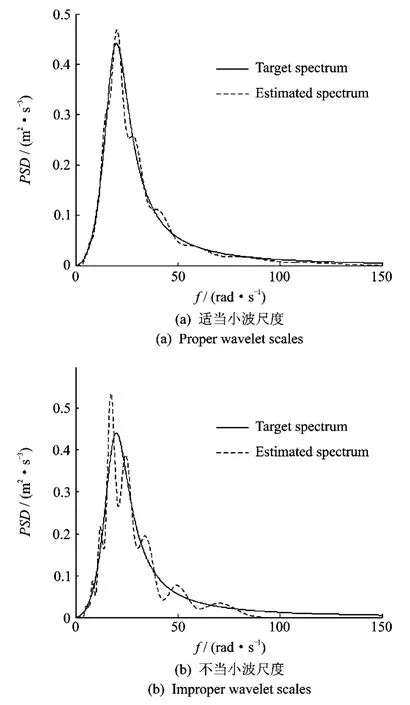
图4 不同小波尺度选择下目标与估计功率谱在7s时的对比Fig．4 Comparisons of target and estimated PSDs at 7s，with different wavelet scales

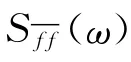
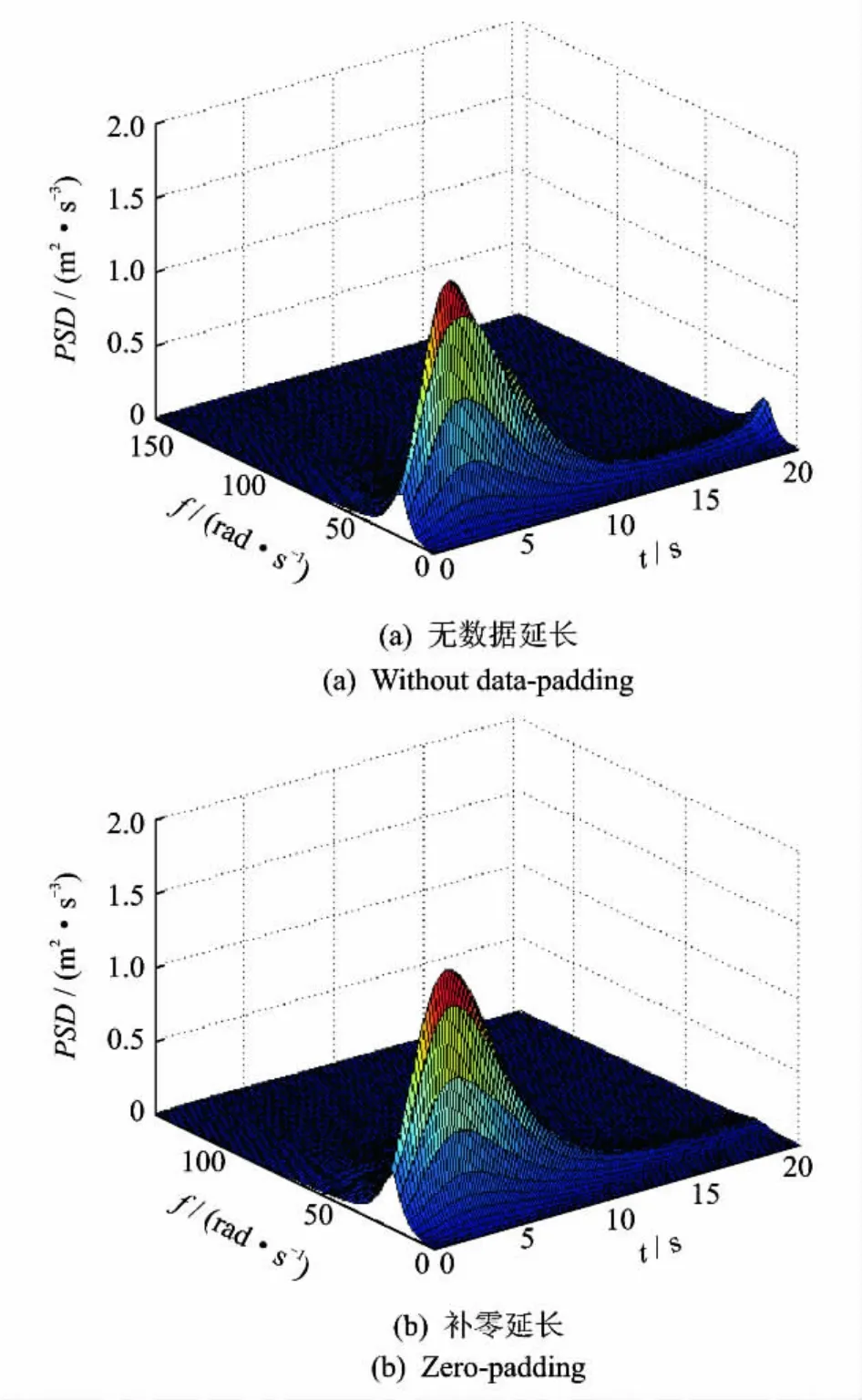
图5 无数据延长和补零延长时非平稳随机过程估计功率谱密度Fig．5 PSD estimations of nonstationary stochastic process with different data－paddings

2 基于局部平稳小波过程的功率谱估计

具有严格数学基础、如式（11）所示的 Wold－Cramer非平稳随机过程模型，根本上是由经典的平稳随机过程的谱分解理论

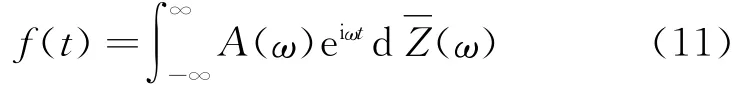
扩展而来，其非平稳性由时间慢变的调制函数A（ω，t）描 述。Dahlhaus 在 非 平 稳 随 机 过 程 的Wold－Cramer模型的同一理论框架下，提出了一种局部平稳过程（Local Stationary Process）［35］。直观地讲，当非平稳随机过程的局部区间能以平稳过程近似表达时，此过程可以称为局部平稳随机过程。由于Dahlhaus模型使用的展开基仍为Fourier基函数，其整体非平稳性由局部平稳的时变传递函数（ω）提供［35，36］。实际上，Fourier其函数由于其频域分辨率很高，却无时间分辨率，本质上无法作为非平稳随机过程模型的基函数；且根据Balian－Low定理，对Fourier基函数加以光滑紧支窗虽然能改善其分辨率，却失去了Fourier基函数的正交性［3］。基于此考虑，Ombao等人在通过对Fourier基函数施加两个特殊构造的光滑窗后，提出了一种在时－频域内紧支且正交的光滑局部指数基（Smooth Localized complex EXponential basis，SLEX），这种基函数可以认为是Fourier基的局部形式［36］。通过以SLEX基代替式（11）中的Fourier基，Ombao等人得到了一种类于式（11）离散形式的非平稳随机过程的SLEX模型。与Dahlhaus模型不同的是，SLEX模型提供了一种对时变功率谱在显式划分的时－频域上分段常数插值的途径［36］。因此，SLEX模型也描述了一种局部平稳的非平稳随机过程。小波基函数由于同时具有一定的时－频域分辨率，Nason等人和Eckley等人提出了一种以非抽样小波为基函数的局部平稳小波过程（Locally Stationary Wavelet process，LSW）［32，33］。实质上，此模型可视为以小波基代替Fourier基后式（11）的离散形式，它直接定义了一种反映非平稳随机过程能量在不同时间－尺度上分布的小波谱。因此本节的出发点在于，如果在LSW模型中引入具有尺度－频率显式关系的小波基，如谐和小波或广义谐和小波，可望得到一种简单的估计非平稳随机过程的时变功率谱密度的方法。

局部平稳小波过程表达为［33］

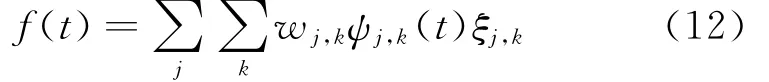
式中ξj，k为归一化正交随机序列；ψj，k为尺度变换和时间平移后的非抽样小波基函数；wj，k为相应尺度和时间处的幅值系数；∑j与∑k分别代表对小波和尺度平移的离散时间点求和。

在如式（12）中的平移时间点和尺度下，上述非平稳随机过程的小波变换为

其中上标＊表示复共轭，且

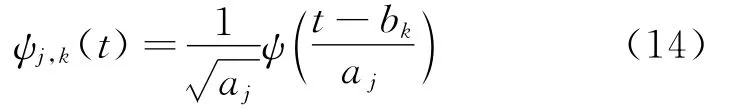
结合式（12）与（13），当LSW 中的小波与式（13）中的小波相同时，则

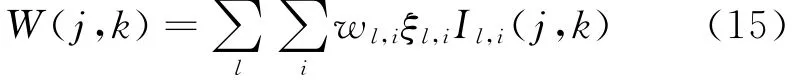
式中Il，i（j，k）为此小波的重建核（Reproducing Kernel）［37］，即

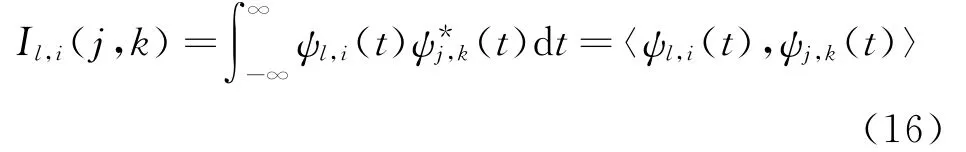
将式（15）两边乘以其复共轭并求期望，在考虑到ξl，i的正交归一性后，可得

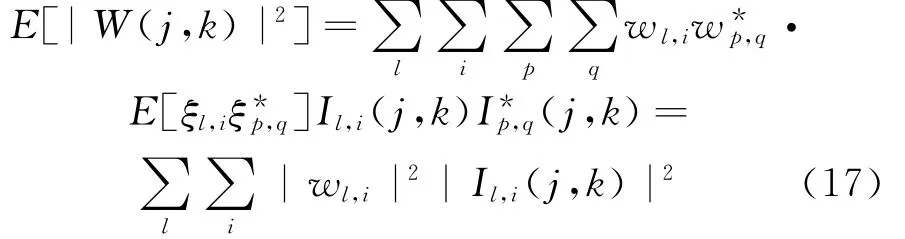
式中 小波的重建核Il，i（j，k）与式（6）中的Qr，s对应。

另一方面，将式（13）两端进行小波内积并求期望［37］，

同时在考虑到小波重建核的性质

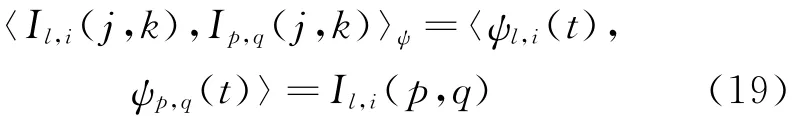
和ξl，i的正交归一性后，式（18）可以写为

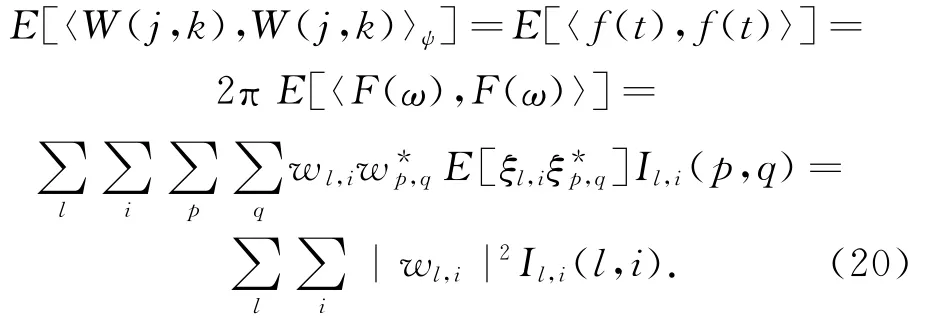
因此，非平稳随机过程的瞬时功率谱表达为

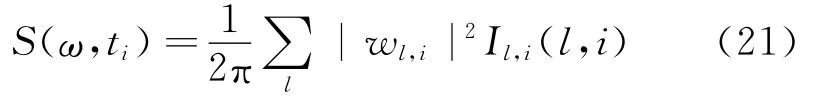
不难看出，非平稳LSW过程的谱估计式（21）与非平稳随机过程演变功率谱估计式（5）类似：前者的时变系数由式（17）求出，后者的时变系数由式（6）求出。因此，二者在形式上可视为是统一的。

当LSW模型中的小波函数为GHW时，考虑到GHW在频域内的性质，易证

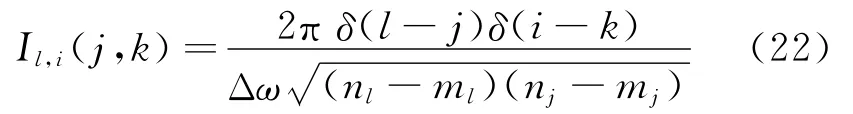
将式（22）代入式（17），得

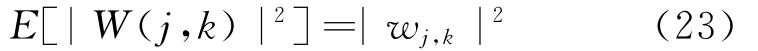
综合式（22）与（23），可证式（21）退化为式（8）。由式（8）可知，两非平稳随机过程的互功率谱密度可以估计为

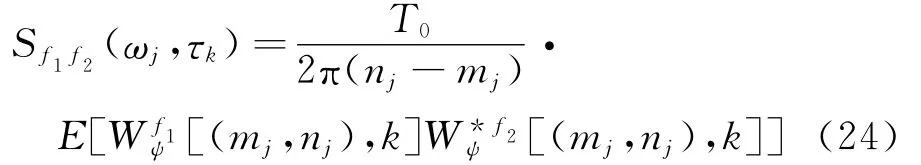
因此，本文所建议方法的意义在于，从数学上解决了LSW非平稳随机过程的时变谱估计问题。对于以GHW为基函数的LSW非平稳随机过程，其时变谱估计方法在形式上与Priestley演变功率谱的GHW估计方法相同。换言之，式（8）不仅适用于Priestley演变功率谱估计，而且适用于基于LSW模型的随机过程时变谱估计。

3 数值算例

3．1 模拟多变量地震动自／互功率谱估计

前已述基于一般小波的非平稳随机过程（Wold－Cramer和LSW非平稳随机过程模型）功率谱估计，以及它们的GHW退化形式，显示了GHW在估计非平稳随机过程时变功率谱方面的优势。为了验证GHW在估计多变量非平稳随机过程互／自功率谱的可靠性，以同一地震中沿地震波主要传播方向分布的3个不同场地为例（如图6所示），在考虑行波效应和场地土条件不同的情况下，估计了三变量非平稳随机过程的互／自演变功率谱密度。场地条件分别为岩石或硬土、低粘性土以及粘性土或细砂。以Clough－Penzien谱表征平稳地震动的功率谱；非平稳随机过程样本由平稳样本乘以考虑行波效应的一致调制函数产生。考虑场地土条件和行波效应的三变量平稳随机过程样本由谱表达方法给出［38］，样本个数为500个，时间步长为Δt＝0．02s，时程取样点为1 024个，谱表达方法的谐和项取为512个，截止频率为 Nyquist频率ωu＝π／Δtrad／s。为了达到时间－频率分辨率的平衡，不同尺度GHW的频宽选择为ni－mi＝12。鉴于篇幅限制，考虑行波效应和场地土条件等参数的多变量谱表达方法在本文中不再重述，其设置可参见文献［38］。

图6 同一地震中的3个不同场地条件Fig．6 Three different site conditions in a same earthquake event

图7（a）～（c）所示分别为硬土、低粘性土及粘性土场地上在6s处的目标与估计自功率谱；图7（d）～（f）所示分别为软粘性土－硬土、低粘性土－硬土及软粘性土－低粘性场地上在6s处的目标与估计互功率谱图。可见，基于GHW能较好地给出多变量非平稳随机过程的自／互功率谱估计。图8（a）～（d）所示为软粘性土和硬土场地上，互谱实部与虚部的目标和估计谱值。限于篇幅，其他场地上自／互谱的实／虚部的目标和估计谱值，兹不一一列出。

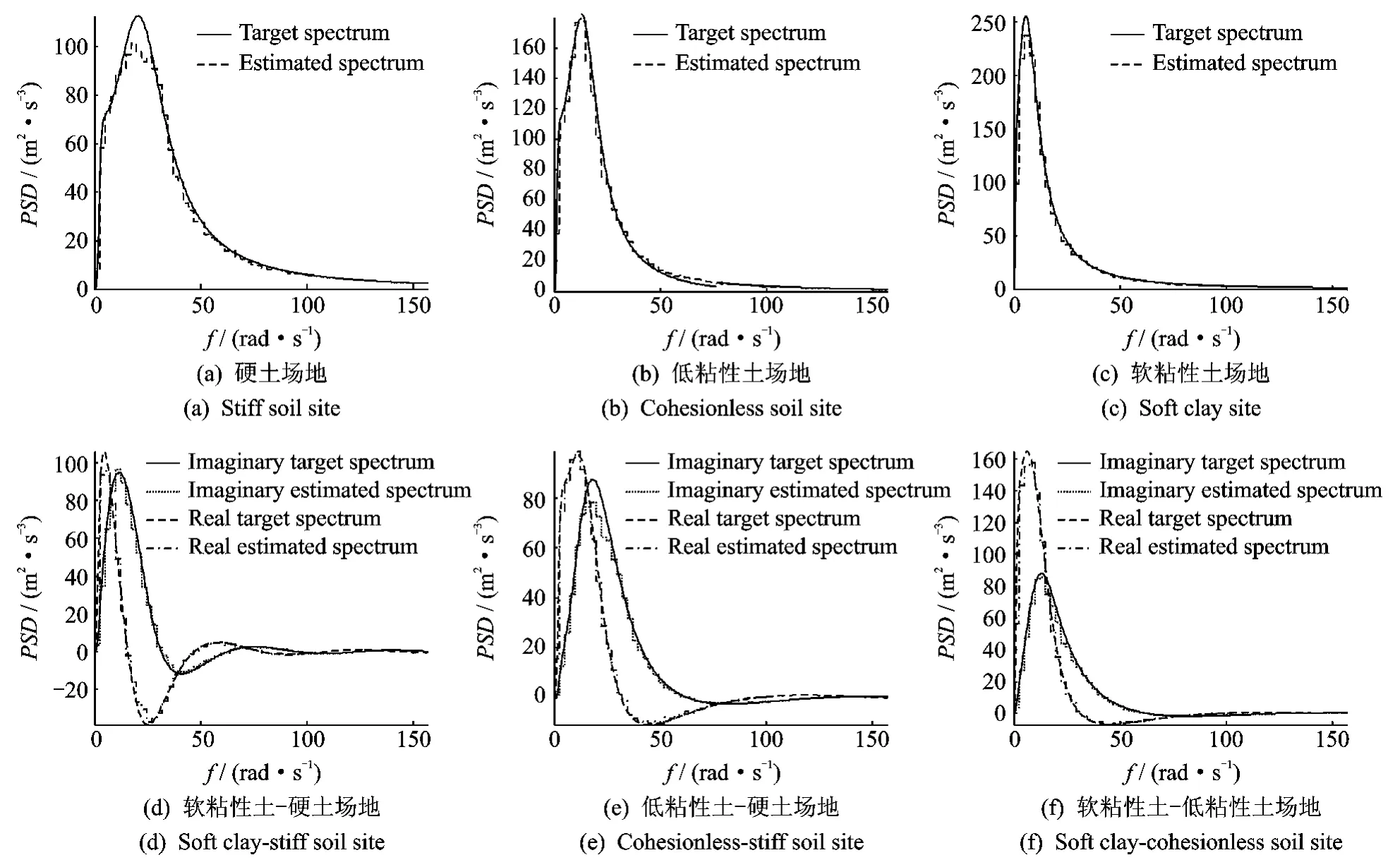
图7 不同场地条件下6s时非平稳地震动瞬时自／互功率谱密度Fig．7 Instantaneous auto／cross－PSDs at 6sof non－stationary ground motion on different sites

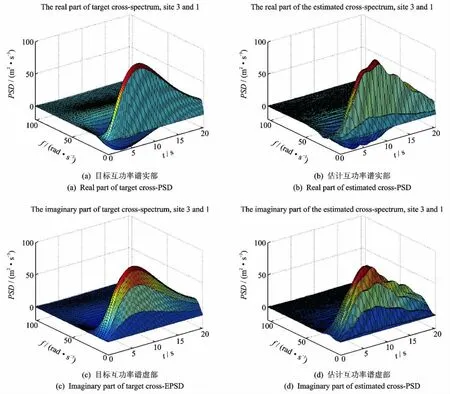
图8 软粘性土和硬土场地上互谱实部与虚部的目标和估计谱值Fig．8 Target and estimated cross－PSDs on soft clay－stiff soil site

最后，以粘性土场地上地震动的自功率谱为例，图9对比了归一化后功率谱密度的0阶矩根，即随机过程目标均方值与估计值对比；表1为各时间点处估计均方值与目标均方值的相对误差。

可见，估计均方相对误差较大处一般发生在地震动开始、峰值以及结尾处，其中以地震动开始处为甚，除此之外，其最大误差均未超过10%。由于在实际工程中更关心的是峰值时间段处随机地震动的统计特性，可见所建议方法精度能满足工程实际需要。

表1 软粘性土场地上各时间点处估计均方值与目标瞬时均方值的相对误差Tab．1 Relative errors between the target and estimated mean sqaure value of the process on the soft clay site

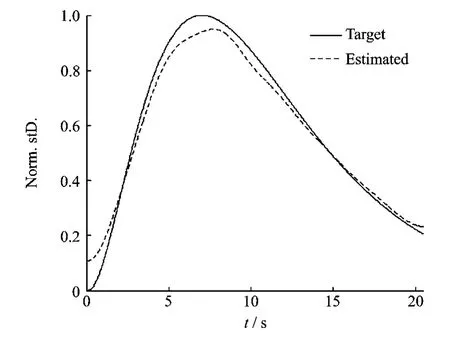
图9 软粘性土场地上归一化估计均方值与目标均方值的对比Fig．9 Comparison of the normalized target and estimated mean square value of the process on the soft clay site

3．2 汶川8．0级地震加速度时程的能量时间－频率分布

本文所建议方法不仅可用于随机过程的时变功率谱估计，而且可以对确定性时程进行时间－频率分析，以得到确定性时程能量的时间－频率分布信息。

2008年5月12日在四川省汶川境内发生了Ms8．0级特大地震，震中位于北纬31．021°，东经103．367°，震源深度14km。本文选取本次地震中离龙门山断层最近（断层距0．74km）的四川绵竹清平台和沿断层破裂方向且离震中较远（震中距637km）的西安台所测得的东西向强震加速度为例，利用本文所建议方法估计了地震动能量的时间－频率分布。图10为两地测得的强震加速度时程；图11为基于GHW变换的两地加速度时程能量的时间－频率分布。

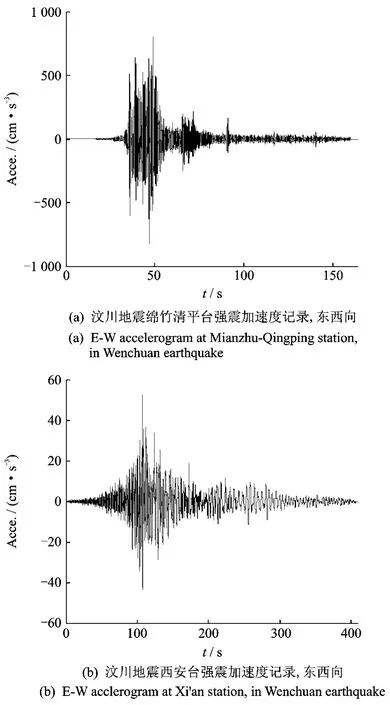
图10 汶川地震中不同场地地震动加速度记录Fig．10 Acceleration records of ground motion in Wenchuan earthquake

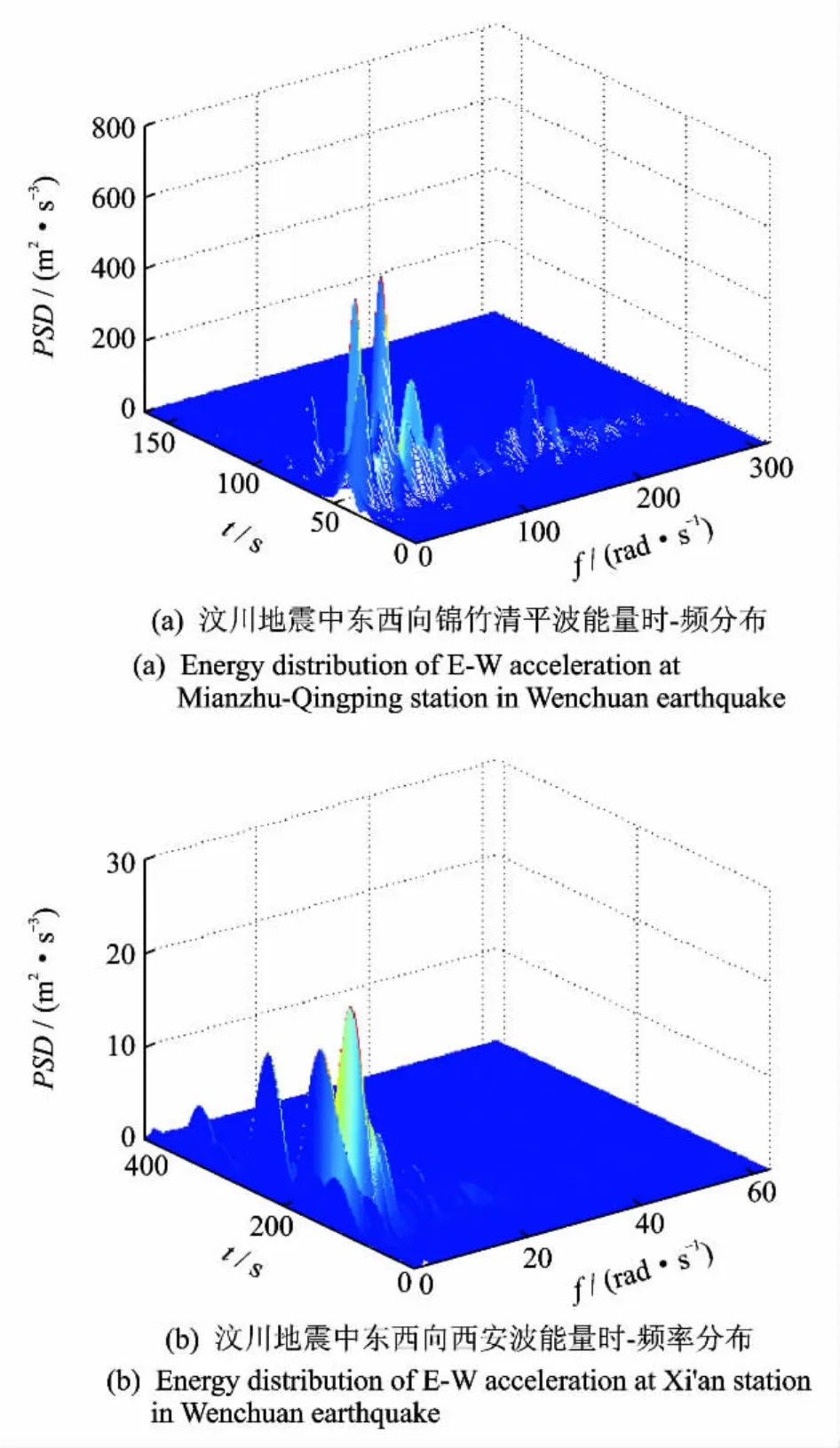
图11 汶川地震动中不同场地上加速度记录能量的时间－频率分布Fig．11 Energy distributions of acceleration records in Wenchuan earthquake

由图10仅能得出两地地震动加速度时程最大值：其中离断层较近的绵竹清平台东西向最大加速度达到了814．13gal，离震中较远的西安台东西向最大加速度只有52．71gal。二者能量的时间－频率分布却有很大不同：前者频域上能量分布较为广泛，有较明显能量的区间为0～200rad／s，主要集中在0～50rad／s范围内，时域上能量主要分布在35～80 s之间，其能量时－频谱主轴主要平行于频率轴，在较短时间内包含了大量频率信息；后者频域上能量分布较前者集中，其中有较明显能量的区间为0～20 rad／s，主要集中在0～5rad／s范围内，时域上能量分布较为广泛，除起震部分时间段外，其他时间段均有明显能量分布，其能量时－频主轴主要平行于时间轴。究其原因，由于前者离震源机制较近，虽然绵竹清平台处于自由场地之上，却仍具有直接来自于震源机制且幅值较大的丰富频率成分，时－频谱表现为时域较窄而频域宽带的特性；反之，西安台处于渭河断裂带附近的第Ⅲ类远场地，由于在传播过程中地震波能量不断被吸收、不同频率成分地震波的频散效应以及场地的过滤作用，致使其时－频谱表现为时间宽带而频域较窄的特性。

4 结 论

本文首先对基于小波的非平稳随机过程演变功率谱密度估计作了若干讨论。指出了小波系数的均方值与演变功率谱密度之间关系式（如式（8）或（10））的应用范围，阐述了此关系式实为Spanos－Failla方法的特殊形式，理清了MLP小波与GHW之间的关系以及它们在估计EPSD应用之中的差别，因此进一步澄清了基于小波估计非平稳随机过程EPSD的物理意义。研究表明，在利用一般小波估计功率谱时，不仅小波的尺度选择至关重要，且非平稳调制函数的慢变特性、小波的边缘效应对估计值也有较大影响。数值试验表明，补零延长能较好地消除边缘效应带来的影响。

根据一种最近提出的随机过程的局部平稳小波过程模型，推导了一种新的非平稳随机过程时变功率谱估计的方法。指出了所建议的新方法与基于Wold－Cramer随机过程模型方法的关联性：二者在形式上是统一的。当基于LSW模型的新方法中的小波基为非抽样广义谐和小波时，此方法退化为Spanos－Tratskas关系式。因此，可以认为Spanos－Tratskas方法不仅可用于 Wold－Cramer模型的非平稳随机过程，而且可应用于任意的随机过程。

为了验证GHW在估计多维非平稳随机过程的可靠性，给出了同一地震中不同场地条件下，在考虑行波效应和不同场地土时，目标与估计自／互功率谱的对比算例。目标瞬时均方值与估计瞬时均方值的对比，显示此方法能满足工程实际的精度要求。最后，以汶川地震中离断层最近的绵竹清平台以及西安台所测得的地震加速度为例，用文中所建议方法对二者进行了加速度能量的时－频谱分析。显示了二者在时－频谱方面的明显不同：前者表现为能量分布时域较窄而频域宽带，后者表现为能量分布时间宽带而频域较窄的特性。

致谢：感谢国家留学基金委（CSC）对本文第一作者在美国Rice大学以联合培养博士研究生进行访问期间给予的资助。

［1］ Trifunac M D．Response envelope spectrum and interpretation of strong earthquake ground motion ［J］．Bulletin of the Seismological Society of America，1971，61（2）：343—356．

［2］ Wang J，Fan L，Qian S，et al．Simulations of non－stationary frequency content and its importance to seismic assessment of structures［J］．Earthquake Engineering＆Structural Dynamics，2002，31（4）：993—1 005．

［3］ Qian S．Introduction to Time－Frequency and Wavelet Transforms［M］．Pretice Hall，2001．

［4］ Qian S，Chen D．Joint Time－frequency Analysis：Methods and Applications［M］．New Jersey：Prentice Hall PTR，1996．

［5］ Gabor D．Theory of communication ［J］．Journal of the IEEE，1946，93（III）：429—457．

［6］ Wexler J，Raz S．Discrete Gabor Expansions［J］．Signal Processing，1990，21（3）：207—220．

［7］ Qian S，Chen D．Discrete Gabor Transform ［M］．New York，NY，ETATS－UNIS：Institute of Electrical and Electronics Engineers，1993．

［8］ Wigner E P．On the quantum correction for the thermodynamic equilibrium ［J］．Physics Review，1932，40：749—759．

［9］ Ville J．Theorie at applications de la notion de signal analytique［J］．Cables Transm，1948（2）：61—74．

［10］Newland D E．An Introduction to Random Vibrations，Spectral and Wavelet Analysis ［M］．New York：Longman Scientific ＆ Technical，1993．

［11］Daubechies I．Ten Lectures on Wavelets［M］．Philadelphia：Society for Industrial and Applied Mathematics，1992．

［12］Mallat S．Multiresolution approximation and wavelets［J］．Tansation of America Mathematics Society，1989，315：69—88．

［13］Grossmann A，Morlet J．Decomposition of Hardy function into square intergrable wavelets of constant shape［J］．SIAM J．Mathematics Anual，1984，15：723—736．

［14］Basu B．Wavelet－based stochastic seismic response of a duffing oscillator［J］．Journal of Sound and Vibration，2001，245（2）：251—260．

［15］Basu B，Gupta V K．Stochastic seismic response of single－degree－of－freedom systems through wavelets［J］．Engineering Structures，2000，22（12）：1 714—1 722．

［16］Basu B，Gupta V K．Seismic response of SDOF systems by wavelet modeling of nonstationary processes［J］．Journal of Engineering Mechanics，1998，124（10）：1 142—1 150．

［17］Iyama J，Kuwamura H．Application of wavelets to analysis and simulation of earthquake motions ［J］．Earthquake Engineering ＆ Structural Dynamics，1999，28（3）：255—272．

［18］Liang J－W，Chaudhuri S R，Shinozuka，M．Simulation of nonostationary stochastic process by spectral representation ［J］．Journal of Engineering Mechanics，2007，133（6）：616—627．

［19］Huang G，Chen X．Wavelets－based estimation of multivariate evolutionary spectra and its application to nonstationary downburst winds ［J］． Engineering Structures，2009，31（4）：976—989．

［20］Newland D E．Practical signal analysis：Do wavelets make any difference？［A］．Proceedings of the 16th ASME Biennial Conference on Vibration and Noise［C］．Sacramento，1997．

［21］Newland D E．Harmonic and musical wavelets［A］．Proceedings：Mathematical and Physical Sciences［C］．1994a：605—620．

［22］Newland D E．Harmonic wavelet analysis［A］．Proceedings of the Royal Society of London．Series A：Mathematical and Physical Sciences［C］．1993：203—225．

［23］Spanos P，Tezcan J，Tratskas P．Stochastic processes evolutionary spectrum estimation via harmonic wavelets［J］．Computer Methods in Applied Mechanics and Engineering，2005，194（12－16）：1 367—1 383．

［24］Tratskas P，Spanos P D．Linear multi－degree－of－freedomsystem stochastic response by using the harmonic wavelet transform ［J］．Journal of Applied Mechanics，2003，70（5）：724．

［25］Tratskas P． Wavelet－based excitation representation and response determination of linear and nonlinear systems［D］．Houston：Rice University，2001．

［26］Spanos P D，Kougioumtzoglou I A．Harmonic wavelet－based statistical linearlization for response evolutionary power spectrum determination．［J］．Probabilistic Engineering Mechanics，2011，doi：10．1016／j．probengmech．2011．05．008．

［27］Priestley M B．Spectral Analysis and Time Series［M］．Academic Press，1981．

［28］Priestley M B．Evolutionary spectra and non－stationary process［J］．Journal of the Royal Statistical Society，Series B，1965，27：204—237．

［29］Spanos P D，Failla G．Evolutionary spectra estimation using wavelets［J］．Journal of Engineering Mechanics，2004，130（8）：952—960．

［30］Chakraborty A，Basu B．Nonstationary response analysis of long span bridges under spatially varying differential support motions using continuous wavelet transform ［J］．Journal of Engineering Mechanics，ASCE，2008，134（2）：155—162．

［31］Failla G，Pappatico M，Cundari G A．A wavelet－based spectrum for non－stationary processes［J］．Mechanics Research Communications，2011，38（5）：361—367．

［32］Eckley I A，Nason G P，Treloar R L．Locally stationary wavelet fields with application to the modeling and analysis of image texture ［J］．Applied Statistics，2010，59：595—616．

［33］Nason G P，von Sachs R，Kroisandt G．Wavelet processes and adaptive estimation of the evolutionary wavelet spectrum ［J］．Journal of the Royal Statistical Society：Series B（Statistical Methodology），2000，62（2）：271—295．

［34］Matz G，Hlawatsch F，Kozek W．Generalized evolutionary spectral analysis and the Weyl spectrum of nonstationary random processes ［M］．New York，NY，ETATS－UNIS：Institute of Electrical and Electronics Engineers，1997．

［35］Dahlhaus R．Fitting time series models to non－stationary processes［J］．The Annals of Statistics，1997，25：1—37．

［36］Ombao H，Raz J，Von Sachs R，et al．The SELX model of a non－stationary random process［J］．Annals of the Institute of Statistical Mathematics，2002，54：171—200．

［37］Rao M R，Bopardkar S A．Wavelet Transforms：Introduction to Theory and Applications ［M］．Massachusetts：Addison Wesley Longman，1998．

［38］Deodatis G．Non－stationary stochastic vector processes：seismic ground motion applications［J］．Probabilistic Engineering Mechanics，1996，11（3）：149—167．