高层建筑结构振动台模型试验与原型对比的研究

钱德玲，李元鹏，刘 杰

（合肥工业大学土木与水利工程学院，安徽 合肥 230009）

引 言

振动台模型试验是研究结构地震破坏机理和破坏模式、评价结构整体抗震能力和衡量减震、隔震效果的重要手段和方法。对于高层和超高层建筑，在理论分析还不完善的情况下，振动台试验是分析其抗震能力的一种有效手段。但由于振动台本身承载能力、试验时间和经费等的限制，对于高层建筑和超高层建筑只能进行缩尺模型试验。为了使模型试验能够准确地反映原型结构的动力特性，必须考虑模型和原型的各物理量的相似关系［1～3］。在结构振动台模型试验中，按照相似理论的要求，设计出与原型结构具有相似工作情况的模型结构［4，5］，但要严格满足相似似理论的全部条件，有时却很难实现，因此有必要对模型结构的相似关系进行研究，并探讨如何由模型试验结果来反映原型结构的动力特性，从而研究和评价原型结构的抗震性能。

本文以12层高层建筑框架结构振动台试验为例，探讨模型和原型结构的相似关系，采用有限元非线性分析软件MSC．Marc建立相关模型，并计算其在地震波作用下的地震反应，根据动力相似关系由模型地震反应反推原型地震反应，将模型反推值与原型计算值进行对比分析，研究原型结构的地震响应，从而验证模型结构动力相似关系的准确性。

1 结构动力相似关系

与结构动力模型相关的主要物理量有［6］：结构的几何尺寸L、结构的位移X、重力加速度g、地震加速度a、质量m、密度ρ、阻尼c、泊松比υ、速度v、转角θ、应力σ、应变ε、弹性模量E、时间t、刚度k、频率ω等。用量纲分析法可写出各物理量在质量系统下的各物理量的量纲矩阵如表1［7］。

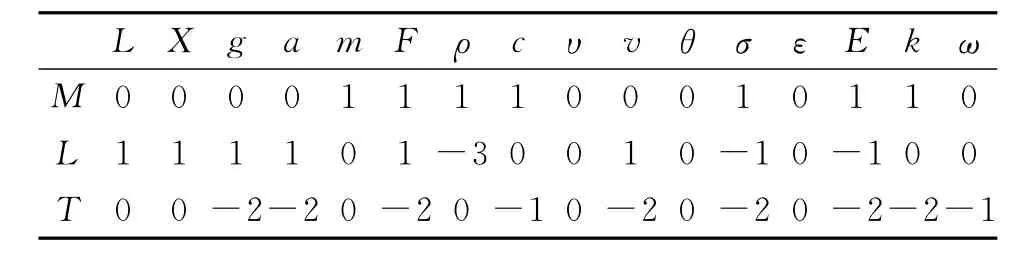
表1 各物理量的量纲矩阵Tab．1 Dimensional matrix of each physical quantity

按照结构模型设计的相似理论，模型与原型必须具有相似的几何以及力学特征（平衡方程、物理方程、几何方程及边界条件等），即描述模型与原型的各个物理量间关系的数学方程应该相同［8］。这就要求模型与原型要做到几何相似、各个物理量间满足一定的相似关系。

在本次结构模型试验设计中，首先确定几何相似系数为SL＝Lp／Lm＝10、密度相似系数为Sρ＝ρp／ρm＝1、结构的弹性模量相似系数为SE＝Ep／Em＝3．76（本文S代表模型和原型各物理量的相似比，角标p表示原型，角标m表示模型），再根据E．Buckinghamπ定理导出其他各物理量的相似关系式和相似系数，见表2。

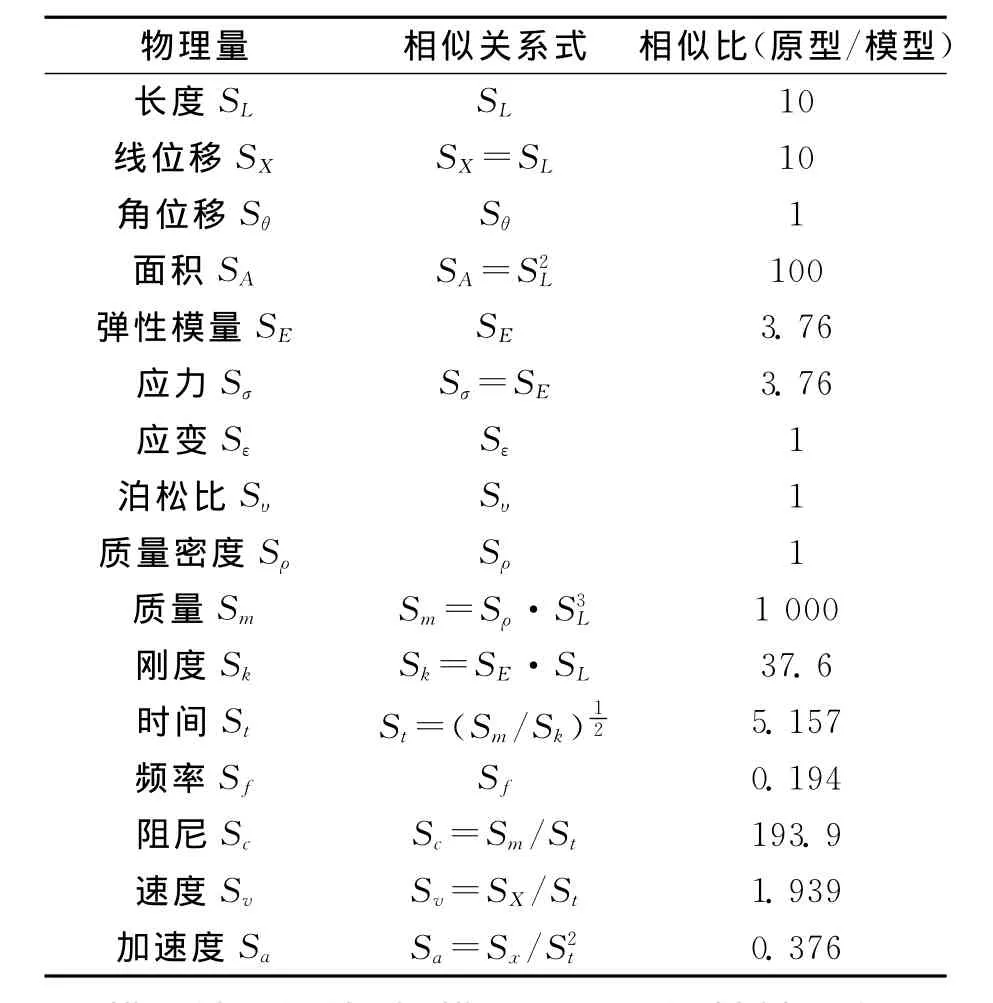
表2 模型结构的动力相似系数Tab．2 Dynamic similarity coefficient of model structure

模型试验设计时，模型所采用的材料要和原型材料的性能相似。本次试验模型用微粒混凝土来模拟原型中上部结构和支盘桩的普通混凝土，用镀锌铁丝模拟原型中的钢筋。其中，微粒混凝土的材料相似关系为：Sfc＝1／Sσ＝1／3．76。原型的混凝土等级为C30，则微粒混凝土强度等级为30／3．76＝7．98，取标号 M8；镀锌铁丝的材料相似关系为：与Ⅱ级钢相比：Sfy＝280／300＝0．933；与Ⅰ级钢相比：Sfy＝280／210＝1．33。

2 原型与模型的尺寸对比

原型结构为单向双跨12层框架结构，层高为3 m，总高为36m；柱子尺寸为500mm×500mm；框架梁截面尺寸为300mm×600mm；框架柱网（2个）为3．4m×5．8m；楼板板厚120mm；承台板尺寸为7m×8m×1m；支盘桩桩长为12m，支盘桩桩径为600mm，支盘盘径为1 400mm。按照相似关系进行模型结构设计，原型与模型结构的尺寸见表3。

表3 原型与模型尺寸对比Tab．3 Comparison of size between prototype and model

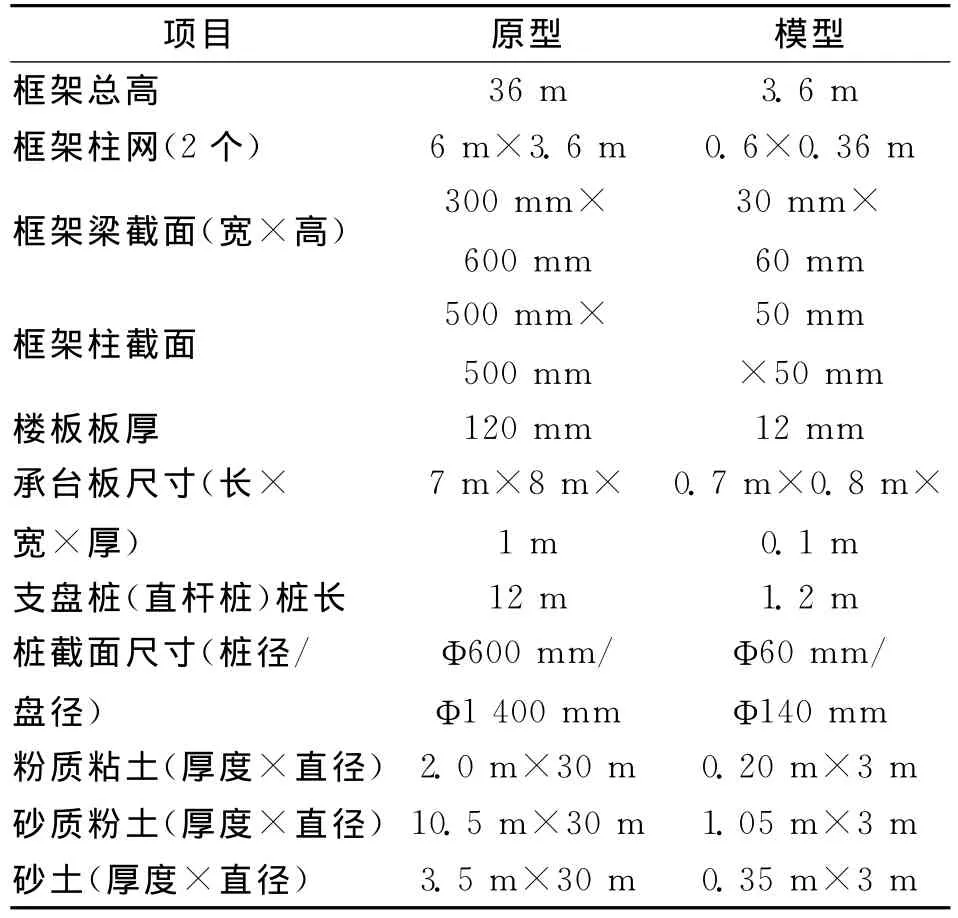
项目 原型 模型框架总高36m 3．6m框架柱网（2个） 6m×3．6m 0．6×0．36m框架梁截面（宽×高） 300mm×600mm 30mm×60mm框架柱截面 500mm×500mm 50mm×50mm楼板板厚 120mm 12mm承台板尺寸（长×宽×厚）0．7m×0．8m×0．1m支盘桩（直杆桩）桩长 12m 1．2m桩截面尺寸（桩径／盘径）7m×8m×1m Φ60mm／Φ140mm粉质粘土（厚度×直径）2．0m×30m 0．20m×3m砂质粉土（厚度×直径）10．5m×30m 1．05m×3m砂土（厚度×直径）Φ600mm／Φ1 400mm 3．5m×30m 0．35m×3m

3 振动台模型试验

该试验于2009年1月在同济大学土木工程防灾国家重点实验室内的MTS三向六自由度模拟振动台上进行。

3．1 模型制作

模型上部框架结构的梁、板、柱均设计为逐层现浇，施工中严格控制构件尺寸和微粒混凝土的配合比。同时模型所用材料均进行材料性能试验，实测材料性能参数。考虑试验的可操作性，动力相互作用体系振动台试验中模型桩基与上部结构采用装配式施工。即将承台板分为上下两部分，上半部分与上部结构一起制作；下半部分与桩一起制作。在下部结构埋入土中后，吊装上部模型结构，两部分间使用螺栓连接。振动台模型试验的施工图及制作完成后的模型见图1所示。

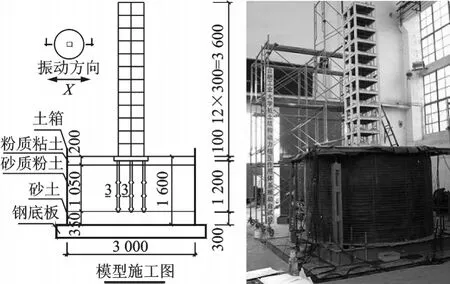
图1 模型施工图及完成后照片（单位：mm）Fig．1 Model structure of drawing and finished photo：（Unit：mm）

3．2 测点布置

试验中采用加速度计、应变计量测上部结构、桩和地基土体的动力响应，对上部结构还采用位移计来测量上部结构的侧移反应，在土中埋置孔隙水压力计量测土的孔隙水压力变化，采用土压力计量测桩土界面的接触压力。

3．3 加载制度

在进行高层建筑结构动力相互作用体系振动台试验之前，首先进行自由场试验，试验台面输入波形采用白噪声、EL Centro波和上海人工波，选择7个工况进行自由场试验。从而得到模型的自振频率、振型以及阻尼比。

自由场试验进行后，静置一天，然后吊装动力相互作用体系的上部结构，进行振动台试验。试验台面输入波形采用EL Centro波、上海人工波和Kobe波，共35个工况。在每次改变加速度输入大小时都输入小振幅白噪声激励，以观察模型的频率和阻尼比的变化情况。输入波形主要为X向激励，部分为Y向，部分工况同时输入X向和Z向激励。台面输入加速度峰值按小量级分级递增，按相似关系调整加速度峰值和时间间隔。

4 有限元分析几何建模

为了对高层建筑振动台试验模型和原型进行对比研究，验证动力相似关系的准确性，需建立原型的有限元分析模型，用来和模型试验值进行对比分析。因此本文采用大型非线性有限元分析软件MSC．Marc对原型结构建立有限元分析模型。

有限元分析软件MSC．Marc具有极强的结构分析能力，可以处理各种线性和非线性结构分析，并提供了丰富的结构单元、连续单元和特殊单元的单元库。分析采用具有高数值稳定性、高精度和快速收敛的高度非线性问题求解技术［9，10］。

在用MSC．Marc进行几何建模时要充分利用结构的对称性，这样可以使结构的有限元模型以及相应的计算规模得到缩减，从而使数据准备工作和计算工作量大幅度地降低［11］。本次建模的桩－土－高层建筑结构动力相互作用体系的几何关于X轴对称，外加地震波动荷载也关于X轴对称，Y＝0平面是该结构体系的对称面。因此几何建模时利用对称性原理，取1／2的原型结构作为研究对象。在对称面上加对称边界条件，以此来保证和实际的边界条件相符合。

建模中，土体、桩、承台以及上部结构均采用三维六面体单元。上部结构划分单元时在梁板柱结点处须保证相邻单元共节点，承台与柱连接处相邻单元也须共节点；土体自上而下分3层划分单元，单元划分时使相邻两层土体的单元共节点，从而保证3层土体单元Merge后是一个整体；支盘桩的单元划分也须保证支盘与直杆交接处单元共节点。原型有限元分析模型如图2所示。

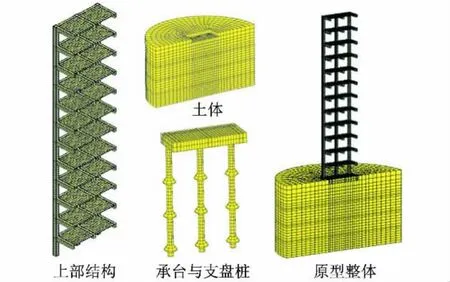
图2 原型有限元分析模型Fig．2 Finite element analysis model of prototype

5 模型与原型结构动力响应的对比

采用大型非线性有限元分析软件MSC．Marc对该高层建筑结构进行有限元动力分析，数值模拟分析时输入EL Centro波，将波的最大幅值调至相当于7度多遇下的加速度峰值，原型结构为0．035g，模型为0．093g。原型结构计算分析时间为16s，时间步长为0．08s，地震波输入方向为X方向。本文仅对在EL Centro波作用下模型结构与原型结构的动力特性和动力响应进行对比分析。

5．1 自振特性对比

原型和模型的前10阶频率对比列于表4。由表4可知：原型结构的计算值与模型反推值（即将模型的自振频率按相似关系反推到原型的自振频率），两者的误差均小于1%，说明模型结构的自振频率能够很好地反映原型结构的自振频率，通过振动台模型试验完全可以用来研究原型结构的动力特性。

由模型试验得到的振型曲线如图3（a）所示，图3（a）中的“1WN”是输入第1工况的白噪声，“12WN”是第12工况的白噪声，以此类推。对原型结构进行模态分析，得到如图3（b）所示的振型图，由图3可知模型与原型结构的振型具有较好的相似性，因此可由模型的振型推算原型结构的振型。

表4 结构自振频率对比Tab．4 Contrast of self－vibration frequency for structure

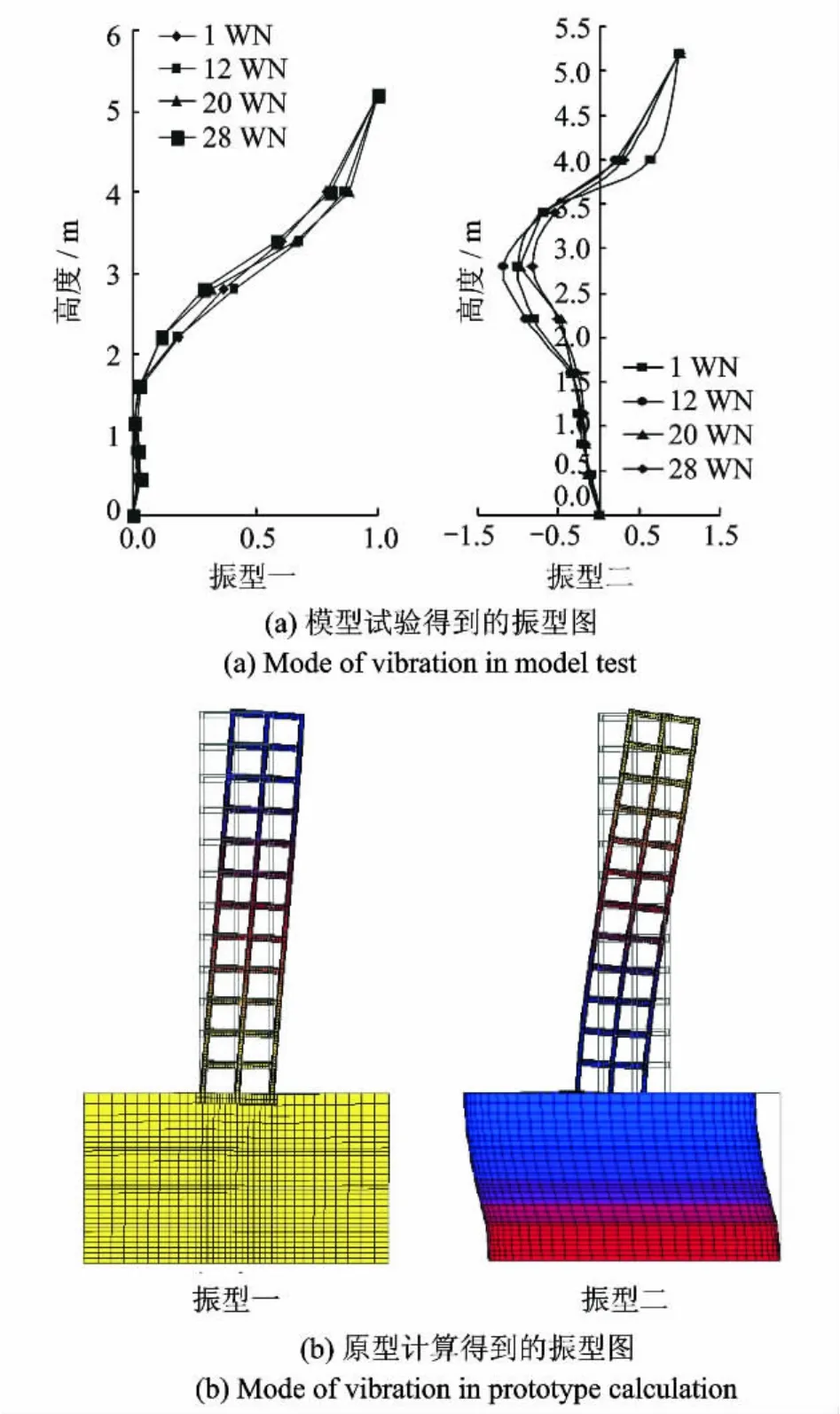
图3 模型试验与原型计算振型对比Fig．3 Contrast of model of vibration between model and prototype

5．2 加速度对比

图4（a）为模型结构顶层在EL Centro地震波作用下的加速度时程曲线，图4（b）为原型结构顶层在EL Centro地震波作用下的加速度时程曲线。图4（a）与（b）曲线变化趋势相同，横轴为时间轴，纵轴为加速度轴。根据模型结构动力相似关系，将图4（a）中横坐标扩大St＝5．157倍，纵坐标缩小Sa＝0．376倍，即将模型加速度反应按相似关系反推到原型结构的加速度反应。图4（c）为模型结构顶层加速度按相似关系的反推值与原型计算值的对比，由图可知模型反推值与原型计算值符合较好。

图4 EL Centro波作用下模型与原型顶层加速度对比Fig．4 Contrast of acceleration between top model and prototype under EL Centro ground motion

通过结构楼层层间最大加速度来对比研究高层建筑结构原型与模型，验证加速度相似关系的正确性。图5（a）为模型在EL Centro波作用下楼层最大加速度值，图5（b）为原型在EL Centro波作用下楼层的最大加速度，将模型加速按加速度相似关系反算到原型结构，即将模型加速度乘以加速度相似系数Sa＝0．376，可得到由模型反推的原型结构楼层最大加速度值，将反推值与原型计算值对比，如图5（c）所示，可见模型反推到的原型与实际原型的计算结果非常接近，具有很好的可比性。说明振动台试验结果及破坏现象可以与原型建筑物相比。

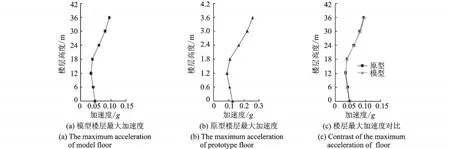
图5 EL Centro波下作用下楼层最大加速度Fig．5 The maximum acceleration of floor under EL Centro ground motion

5．3 位移对比

模型顶层在EL Centro地震波作用下的位移时程曲线如图6（a）所示，图6（b）为原型顶层在EL Centro地震波作用下的位移时程曲线，图6（a）和（b）中结构顶层位移曲线的变化趋势相同。将图6（a）中横坐标按时间相似关系扩大St＝5．157倍，纵坐标按线位移相似关系扩大SX＝10倍，所得值与图6（b）相对应。将模型反推值与原型计算值对比，如图6（c）所示，二者非常符合，从而验证了位移相似关系的准确性，因此可以由模型的位移反应来反推原型结构的位移反应。

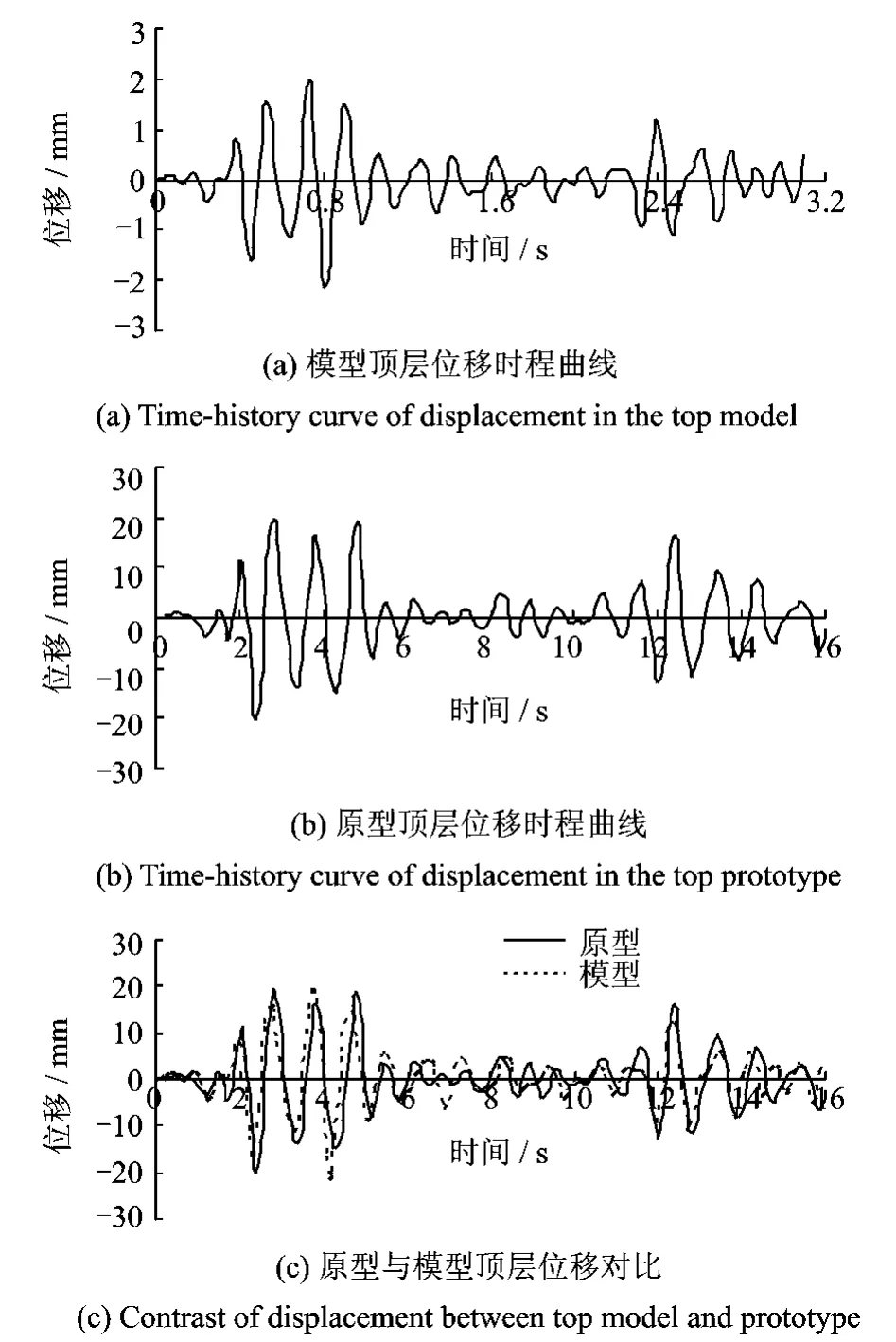
图6 EL Centro波作用下模型与原型顶层位移对比Fig．6 Contrast of displacement between top model and prototype under EL Centro ground motion

在EL Centro波作用下，对比高层建筑结构原型与模型的楼层最大侧移，图7（a）为模型结构楼层在X向的最大侧移值，图7（b）为原型结构的楼层最大位移值，将模型结构的楼层最大位移按照位移相似关系乘以相似系数SX＝10可推得原型结构的楼层最大位移，并将其反推值与原型结构计算值对比，如图7（c）所示，可见由模型反推得到的位移值和原型计算值相符合。

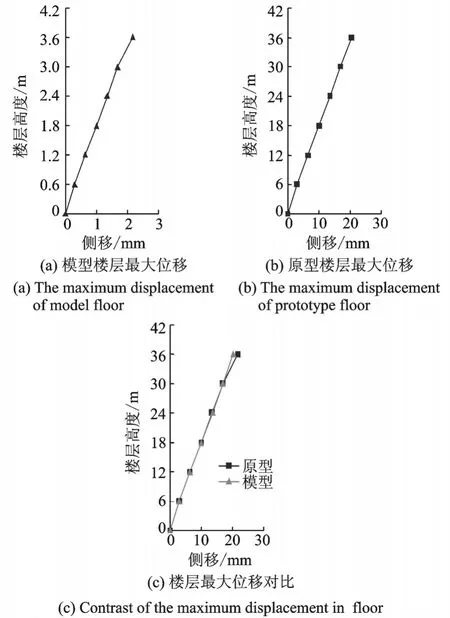
图7 EL Centro波作用下结构楼层最大位移Fig．7 The maximum displacement of the structure under EL Centro ground motion

5．4 剪力对比

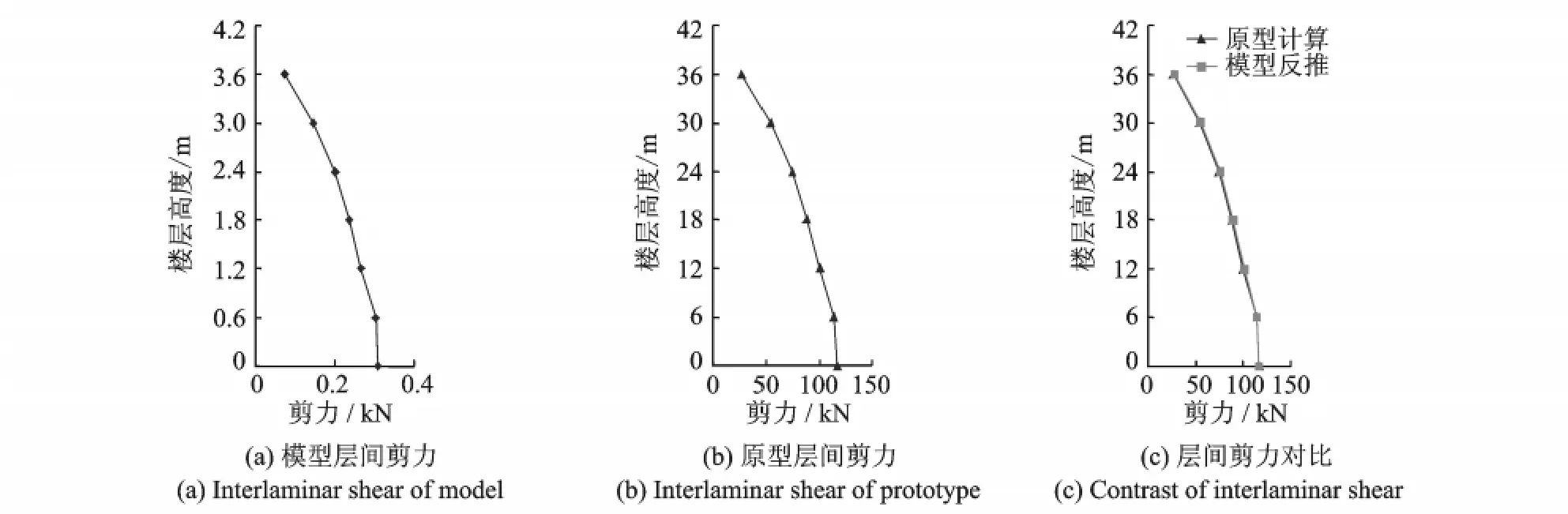
图8 EL Centro波作用下结构层间剪力对比Fig．8 Contrast of interlaminar shear under EL Centro ground motion

6 结 论

（1）对比模型和原型的前10阶自振频率，模型反推值和原型计算值符合较好；由模型试验得到的振型曲线和原型的模态分析得到的振型相似性较好，故可采用模型试验结果来研究原型结构的动力特性。

（2）按相似关系，由模型反推得到原型的加速度和按原型结构的计算值相符合，对于框架结构的加速度放大系数也有较好的相似性，结构顶层最大加速度放大系数：模型为2．09，原型为2．01。

（3）按相似关系由模型推导的原型结构顶层最大位移为21．66mm，按原型结构计算的结构顶层最大位移为20．36mm，二者误差不大，水平总位移角为1／1 662，满足最大层间位移角1／550的要求［12］。

（4）根据相似关系反推得到的原型结构底部的剪力为116．386kN，按原型结构计算分析得到的为116．593kN，可见其剪力也相当符合。

通过上述对高层建筑结构模型和原型的频率、振型、加速度、位移和剪力的对比分析，验证了基于E．Buckinghamπ定理导出的动力相似关系的准确性，振动台模型试验可以真实地反映原型的地震响应，可以根据模型的试验结果对原型结构进行抗震性能的评估。

［1］ 张敏政．地震模拟实验中相似律应用的若干问题［J］．地震工程与工程振动，1997，17（2）：52—58．

Zhang Minzheng．Study on similitude laws for shaking table tests［J］．Earthquake Engineering and Engineering Vibration，1997，17（2）：52—58．

［2］ 沈德建，吕西林．地震模拟振动台及模型试验研究进展［J］．结构工程师，2006，22（6）：55—58，63．

Shen Dejian，Lv Xilin．Research advances on simulating earthquake shaking tables and model test ［J］．Structure Engineers，2006，22（6）：55—58，63．

［3］ 施卫星，丁美，成广伟，等．超高层建筑整体模型模拟地震振动台试验研究［J］．四川大学学报（工程科学版），2007，39（4）：50—56．

Shi Weixing，Ding Mei，Cheng Guangwei，et al．Shaking table model test of a high－rise building structure［J］．Journal of Sichuan University （Engineering Science Edition），2007，39（4）：50—56．

［4］ 吕西林．复杂高层建筑结构抗震理论与应用［M］．北京：科学出版社，2007．

Lv Xilin．Complex High－rise Building Structure Seismic Theory and Application［M］．Beijing：Science Press，2007．

［5］ 郑山锁．动力试验模型在任意配重条件下与原型结构的相似关系［J］．工业建筑，2000，30（3）：35—39．

Zheng Shangsuo．Analogical ratio between scale models withless ballast and their prototypes under shaking table test［J］．Industrial Buildings，2000，30（3）：35—39．

［6］ 王天稳．土木工程结构试验［M］．武汉：武汉理工大学出版社，2006．

Wang Tianwen．Civil Engineering Structure Test［M］．Wuhan：Wuhan University of Science and Technology Press，2006．

［7］ 徐挺．相似理论与模型试验［M］．北京：中国农业机械出版社，1982．

Xu Ting．Similarity Theory and Model Test［M］．Beijing：China′s Agricultural Mechanical Press，1982．

［8］ 张昕，周德源，张风岭，等．某高层建筑结构模型振动台试验研究及有限元分析［J］．地震工程与工程振动，1999，19（3）：37—43．

Zhang Xin，Zhou Deyuan，Zhang Fengling，et al．Shaking table test and finite element analysis of a complex high－rise building structure model［J］．Earthquake Engineering and Engineering Vibration，1999，19（3）：37—43．

［9］ 陈火红，杨剑，薛小香，等．新编 Marc有限元实例教程［M］．北京：机械工业出版社，2007．

Chen Huohong，Yang Jian，Xue Xiaoxiang，et al．New MARC Finite Element Instance Tutorial［M］．Beijing：Machinery Industry Press，2007．

［10］阙前华，常志宇．MSC．Marc工程应用实例分析与二次开发［M］．北京：中国水利水电出版社，2005．

Que Qianhua，Chang Zhiyu．MSC．Marc Examples of Engineering Application Analysis and Secondary Development［M］．Beijing：China Water Conservancy and Hydropower Press，2005．

［11］梁清香．有限元与 MARC实现［M］．北京：机械工业出版社，2005．

Liang Qingxiang．Finite Element and MARC to Realize［M］．Beijing：Machinery Industry Press，2005．

［12］中华人民共和国住房和城乡建设部．GB 50011－2010建筑抗震设计规范［S］．北京：中国建筑工业出版社，2010．

Ministry of Housing and Urban－Rural Construction of the People＇s Republic of China．Code for Seismic Design of Buildings（GB50011－2010）［S］．Beijing：China Architecture ＆Building Press，2010．